Публикую первую часть второй главы лекций по теории
автоматического управления.
В данной статье рассматриваются:
2.1. Получение уравнений динамики системы. Статическая характеристика. Уравнение динамики САУ (САР) в отклонениях
2.2. Линеаризация уравнений динамики САУ (САР)
2.3. Классический способ решения уравнений динамики
Лекции по курсу Управление Техническими Системами, читает Козлов Олег Степанович на кафедре Ядерные реакторы и энергетические установки, факультета Энергомашиностроения МГТУ им. Н.Э. Баумана. За что ему огромная благодарность.
Данные лекции только готовятся к публикации в виде книги, а поскольку здесь есть специалисты по ТАУ, студенты и просто интересующиеся предметом, то любая критика приветствуется.
Первая часть: Введение в теорию автоматического управления. Основные понятия теории управления техническим системами
2.1. Получение уравнений динамики системы. Статическая характеристика. Уравнение динамики САУ (САР) в отклонениях
При составлении уравнений, описывающих нестационарные процессы в САУ (САР) и которые в дальнейшем будем называть уравнениями динамики, система разбивается на отдельные элементы (звенья), для каждого из которых не существует проблем в записи соответствующего уравнения динамики.
На рис. 2.1.1 представлено схематичное представление САУ (звена) в переменных вход-выход, где x(t) (или u(t)) входное воздействие, а y(t) выходное воздействие, соответственно. Нередко входное воздействие будет называться управляющим, а выходное воздействие регулируемой величиной (переменной).

Рис. 2.1.1 Схематическое представление САУ (звена)
При составлении уравнений динамики используются фундаментальные законы сохранения из разделов Механики, Физики, Химии и др.
Например, при описании перемещения узла какого-то механизма силового привода используются законы сохранения: момента, энергии, импульса и др В теплофизических (теплогидравлических) системах используются фундаментальные законы сохранения: массы (уравнение неразрывности), импульса (уравнение движения), энергии (уравнение энергии) и др
Уравнения сохранения в общем случае содержат постоянные и нестационарные члены, причем при отбрасывании нестационарных членов получают так называемые уравнения статики, которые соответствуют уравнениям равновесного состояния САУ (звена). Вычитанием из полных уравнений сохранения стационарных уравнений получают нестационарные уравнения САУ в отклонениях (от стационара).
где:
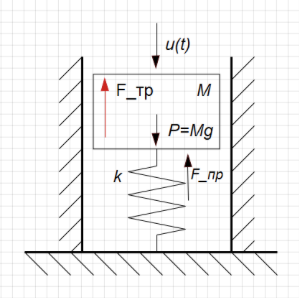
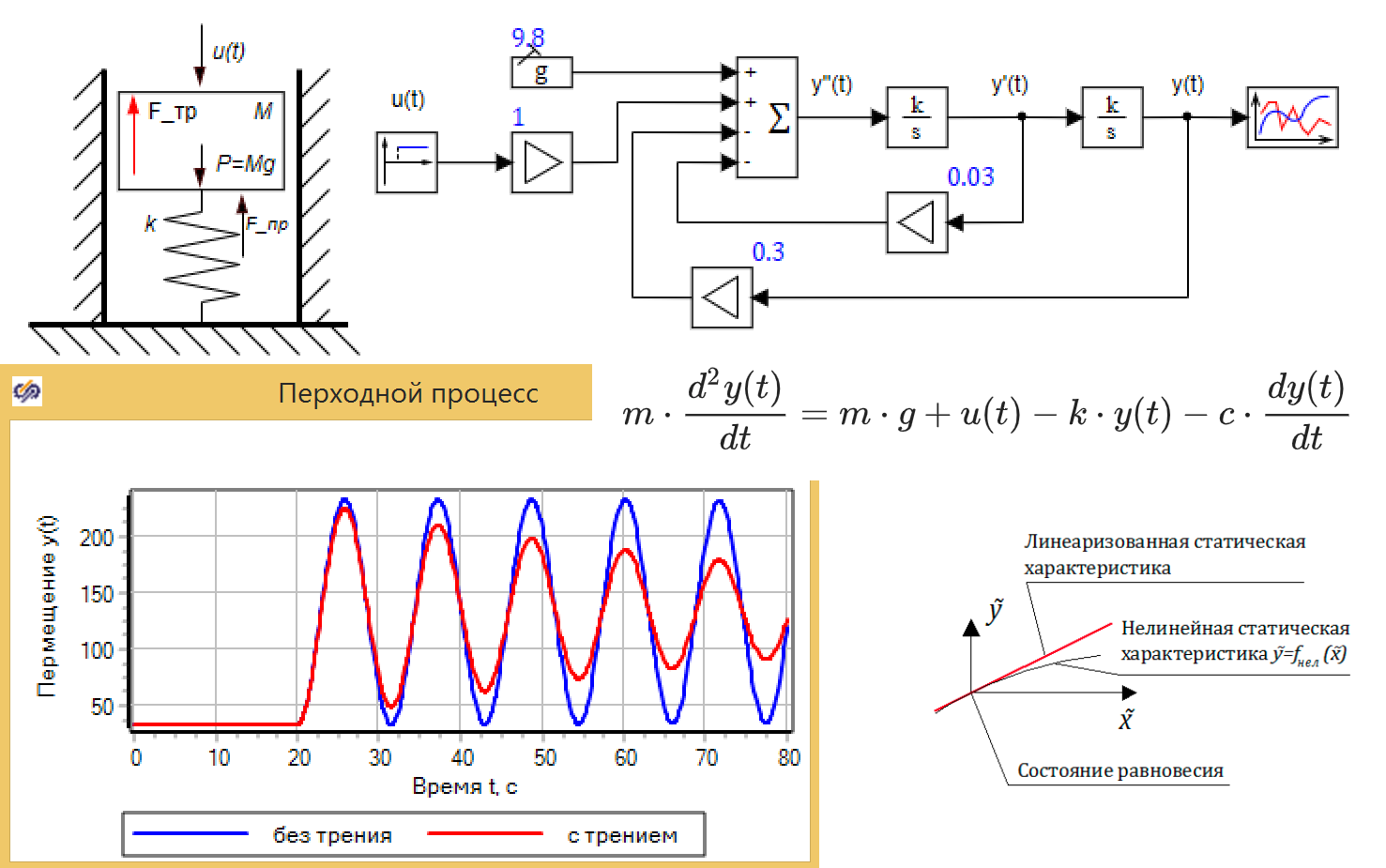
В качестве примера рассмотрим технологию получения уравнений динамики для механического демпфера, схематическое изображение которого представлено на рис. 2.1.2.

Рис. 2.1.2 Механический демпфер
Согласно 2-му закону Ньютона, ускорение тела пропорционально сумме сил, действующих на тело:
где, m масса тела, Fj все силы воздействующие на тело (поршень демпфера)
Подставляя в уравнение (2.1.1) все силы согласно рис. 2.2, имеем:
где сила тяжести;
сила сопротивления пружины,
сила вязконо
трения (пропорциональна скорости поршеня)
Размерности сил и коэффициентов, входящих в уравнение (2.1.2):
$$display$$\left \{ \begin{eqnarray} t &\le 0 \\ u(t) &= u_0\\ y(t) &= y_0\\ \end{eqnarray} \right.$$display$$
перейдем к отклонениям от стационарного состояния:Пусть при t>0
если
Соотношение (2.1.4) уравнение звена (демпфера) в равновесном (стационарном) состоянии, а соотношение (2.1.5) статическая характеристика звена демпфера (см. рисунок 2.1.3).

Рис. 2.1.3 Статическая характеристика механического демпфера
Вычитая из уравнения (2.1.3) уравнение (2.1.4), получаем
уравнение динамики демпфера в отклонениях:
тогда, разделив на k, имеем:
где:
Уравнение (2.1.6) это уравнение динамики в канонической форме, т.е. коэффициент при y(t) равен 1.0!
Легко видеть, что коэффициенты перед членами, содержащими производные, имеют смысл (и размерность!) постоянных времени. В самом деле:
Таким образом, получаем, что:
коэффициент перед первой производной имеет размерность [c] т.е.
смысл некоторой постоянной времени;
коэффициент перед второй производной: [];
коэффициент в правой части (): [
].
Тогда уравнение (2.1.6) можно записать в операторной форме:
Анализ уравнения (2.1.6.а) показывает, что такое уравнение имеет размерные переменные, а также размерными являются все коэффициенты уравнения. Это не всегда удобно. Кроме того, если реальная САР (САУ) состоит из многих звеньев, выходными воздействиями которых являются различные физические переменные (скорость, температура, нейтронный поток, тепловой поток и т.д.), то значения коэффициентов могут различаться на большое число порядков, что ставит серьезные математические проблемы при численном решении уравнений динамики на компьютере (поскольку числа в компьютере всегда представляются с какой-то точностью). Одним из наилучших способов избежать численных трудностей является принцип нормализации, т.е. переход к безразмерным отклонениям, которые получены нормированием отклонения на стационарное значение соответствующей переменной.
Введем новые нормированные (безразмерные) переменные:
Подставляя эти соотношения в уравнение (2.1.2), имеем:
Поддчеркнутые члены выражения в сумме дают 0 (см. 2.1.4) Перенося в левую часть члены, содержащие
где:
Проверим размерность коэффициента
Использованный выше технический прием позволяет перейти к безразмерным переменным, а также привести вид коэффициентов в уравнении динамики к легко интерпретируемому виду, т.е. к постоянным времени (в соответствующей степени) или к безразмерным коэффициентам усиления.
На рис. 2.1.4 представлены статические характеристики для механического демпфера:

Рис. 2.1.4 Статические характеристики механического демпфера
Процедура нормировки отклонений позволяет привести уравнения динамики к виду:
Если дифференциальные операторы линейные, а
статическая характеристика САУ (звена) тоже линейна, то выражение
(2.1.8) соответствует линейному обыкновенному
дифференциальному уравнению (ОДУ).
А если нелинейные
дифференциальные операторы, или
, то уравнение динамики нелинейное. Под
нелинейными действиями понимаются все математические действия,
кроме сложения (+) и вычитания (-).
Пример создания модели демпфера можно посмотереть здесь: Технология получения уравнений динамики ТАУ
2.2. Линеаризация уравнений динамики САУ (САР)
Практически все реальные системы автоматического управления (САУ) являются нелинейными, причем нелинейность САУ может определяться различным причинами:
- Нелинейностью статической характеристики.
- Нелинейностью динамических членов в уравнениях динамики.
- Наличием в САУ принципиально нелинейных звеньев.
Если в замкнутой САУ (САР) нет принципиально нелинейных звеньев, то в большинстве случаев уравнения динамики звеньев, входящих в систему, могут быть линеаризованы. Линеаризация основана на том, что в процессе регулирования (т.е. САУ с обратной связью) все регулируемые величины мало отклоняются от их программных значений (иначе система регулирования или управления не выполняла бы своей задачи).
Например, если рассмотреть управление мощностью энергетического ядерного реактора, то главная задача САР поддержание мощности на заданном (номинальном) уровне мощности. Существующие возмущения (внутренние и внешние) отрабатываются САР и поэтому параметры ядерного реактора незначительно отличаются от стационарных. На рис. 2.2.1 представлена временная зависимость мощности ядерного реактора, где нормированные отклонения мощности N /N0 << 1, и поэтому уравнения динамики ядерного реактора, в принципе, могут быть линеаризованы.

Рис. 2.2.1 Пример изменения мощности реактора
Рассмотрим некоторое звено (или САР в целом), описание динамики которого можно представить в переменных вход-выход:

Рис. 2.2.2 Звено САР
Предположим, что динамика данного звена описывается обыкновенным дифференциальным уравнением n-го порядка:
Перенесем в левую часть уравнения и
запишем уравнение в виде%
где - функция регулируемой переменной и ее
производных, а также управляющего (входного) воздействия и его
производных, причем F обычно нелинейная функция.
Будем считать, что при t 0 САУ (звено) находилось в равновесии (в стационарном состоянии). Тогда уравнение (2.2.2) вырождается в уравнение статической характеристики:
Разложим левую часть уравнения (2.2.2) в ряд Тейлора в малой
окрестности точки равновесного состояния .
Напомним, что разложение в ряд Тейлора трактуется следующим
образом: если , то простое разложение функции
в ряд Тейлора в окрестности точки
будет выглядеть так:
C учетом вышеприведенного разложение принимает вид:
Предполагая, что отклонения выходных и входных воздействий
незначительны, (т.е.:), оставим в разложении только члены первого
порядка малости (линейные). Поскольку
, получаем:
Подставляя соотношение (2.2.4) в уравнение (2.2.2), и перенося множители при у и u в разные части получаем уравнения:
Коэффициенты постоянные коэффициенты,
поэтому уравнения 2.2.5 линейное дифференциальное с постоянными
коэффициентами.
В дальнейшем нами будет часто использоваться операторная форма записи уравнений динамики:
где
Уравнения (2.2.5) и (2.2.6) уравнения динамики системы (звена) в отклонениях.
Если исходное уравнение (2.2.1) дифференциальное уравнение в
физических переменных (температура, скорость, поток и т.д.), то
размерность коэффициентов может быть произвольной
(любой).
Переход к нормализованным отклонениям позволяет упорядочить
размерность коэффициентов. В самом деле, разделив уравнение (2.2.5)
на и выполнив некоторые
преобразования, получаем:
Приведение уравнения динамики САУ (звена) к нормализованному виду позволяет унифицировать размерность коэффициентов уравнений: ==>
$$display$$[a_0^*] = [1] ;\ \ [a_1^*]= [c];\ \ [a_2^*]= [c^2];\ \ [a_3^*]= [c^3];...[a_n^*]= [c^n]\\ [b_0^*] = [1] ;\ \ [b_1^*]= [c];\ \ [b_2^*]= [c^2];\ \ [b_3^*]= [b^3];...[b_m^*]= [c^m]$$display$$
Если вынести в правой части (2.2.7) коэффициент за общую скобку и разделить все
уравнение на
, то уравнение принимает вид:
где:
Линеаризация уравнений динамики и нормализация переменных позволяют привести уравнения динамики САУ (звена) к виду, наиболее удобному для использования классических методов анализа, т.е. к нулевым начальным условиям.
$$display$$Если \ t 0 \Rightarrow \left[ \begin{gathered} \tilde {y}(t) = \tilde {y}(0) =0;\\ \tilde u(t) = \tilde u(0) = 0.\\ \end{gathered} \right.$$display$$
Пример
Выполнить линеаризацию уравнения динамики некоторой абстрактной САР в окрестности состояния (x0, y0), если полное уравнение динамики имеет вид:
Нелинейность полного уравнения динамики проявляется в следующем:
во-первых, в нелинейности статической характеристики:

Рис. 2.2.3 Линеаризации статической характеристики
во-вторых, слагаемое в левой части чисто
нелинейное, так как действие умножения является нелинейным.
Выполним процесс линеаризации исходного уравнения, динамики без разложения я ряд Тейлора, основываясь на том, что в окрестности состояния (x0, y0) нормированные отклонения управляющего воздействия и регулируемой величины намного меньше 1.
Преобразования выполним в следующей последовательности:
- Перейдем к безразмерным переменным (нормализованным);
- Выполним линеаризацию, отбросив нелинейные члены 2-го и выше порядков малости.
Перейдем к новым безразмерным переменным:
Заметим, что:.
Подставляя значения x(t) и y(t) в исходное уравнение:
Удаляем полученного уравнения уравнения стационара: , а
так же пренебрегая слагаемыми второго прядка малости:
, получаем следующее уравнение:
Вводим новые обозначения:
Получаем уравнения в почти классическом виде:
Если в правой части вынести за общую скобку и разделить все уравнение на
, то уравнение (линеаризованное)
принимает вид:
где:
Процедура нормализации позволяет более просто линеаризовать уравнение динамики, так как не требуется выполнять разложение в ряд Тейлора (хотя это и не сложно).
2.3. Классический способ решения уравнений динамики
Классический метод решения уравнений динамики САУ (САР) применим только для линейных или линеаризованных систем.
Рассмотрим некоторую САУ (звено), динамика которой описывается линейным дифференциальным уравнением вида:
Переходя к полной символике, имеем:
Выражение (2.3.2) обыкновенное дифференциальное уравнение (ОДУ), точнее неоднородное ОДУ, так как правая часть 0.
Известно входное воздействие x(t), коэффициенты уравнения и начальные условия (т.е. значения переменных и производных при t = 0).
Требуется найти y(t) при известных начальных условиях.
Известно, что
где: решение однородного
дифференциального уравнения
y_{част.}(t) $inline$ -
частное решение. $inline$
Будем называть решение однородного дифференциального
уравнения , собственным
решением, так как его решение не зависит от входного
воздействия, а полностью определяется собственными
динамическими свойствами САУ (звена).
Вторую составляющую решения (2.3.3) будем называть , вынужденным, так
как эта часть решения определяется внешним воздействием
, поэтому САУ (САР или звено)
вынуждена отрабатывать это воздействие:
Напомним этапы решения:
1) Если имеется уравнение вида , то сначала
решаем однородное дифференциальное уравнение:
2) Записываем характеристическое уравнение:
3) Решая уравнение (2.3.5), которое является типичным степенным
уравнением, каким-либо способом (в том числе и с помощью
стандартных подпрограмм на компьютере) находим корни
характеристического уравнения
4) Тогда собственное решение записывается в виде:
если среди нет повторяющихся корней
(кратность корней равна 1).
Если уравнение (2.3.5) имеет два совпадающих корня, то собственное решение имеет вид:
Если уравнение (2.3.5) имеет k совпадающих корней (кратность корней равна k), то собственное решение имеет вид:
5) Вынужденную часть решения можно найти различными способами,
но наиболее распространены следующие способы:
а) По виду правой части.
б) Методом вариации постоянных.
в) Другие методы
Если вид правой части дифференциального уравнения относительно
несложная функция времени, то предпочтительным является способ а):
подбор решения. .
6) Суммируя полученные составляющие (собственную и вынужденную),
имеем:
7) Используя начальные условия (t = 0), находим значения
постоянных интегрирования .
Обычно получается система
алгебраических уравнений.
Решая систему, находим
значения постоянных интегрирования
Пример
Найти аналитическое выражение переходного процесса на выходе звена, если
Решение. Запишем однородное ОДУ:
Характеристическое уравнение имеет вид: ; Решая, имеем:
тогда:
где
По виду временной функции в правой части запишем как:
Подставляя в исходное уравнение, имеем:
Суммируя , имеем:
Используя 1-е начальное условие (при t = 0), получаем: , а из 2-го начального
условия имеем:
Решая систему уравнений относительно и
, имеем:
Тогда окончательно:
Что бы проверить результ, выполним моделирование процесса в SimInTech, для этого преобразуем исходное уравнение к виду:
Создадим модель SimInTech, содержащую исходное динамическое уравнение и полученное аналитическое решение, и выведем результаты на один график (см. рис. 2.3.1).

Рис. 2.3.1 структурная схема для проверки
решения
На рис. 2.3.2 приведено решение по вышеприведенному соотношению и численное решение задачи в среде SimInTech (решения совпадают и линии графиков наложены друг на друга).

Рис. 2.3.2 Решение уравнения динамики
Ссылки по теме: