Векторы

Мотивация

Это рассказ о том, что такое внешняя алгебра, из чего она состоит. Удивительно, но на Хабре почти нет статей о внешней алгебре при том, что ее прикладная ценность ничуть не меньше, например, реляционной алгебры. Внешняя алгебра - это смесь теории множеств, алгебры и комбинаторики. Она является основой для понимания пространств, поэтому в той или иной степени присутствует почти во всех разделах математики. При том, что ее постулаты исключительно просты.

Наше изложение отличается от традиционного, - ориентируемся не столько на точность формулировок, сколько на передачу сути. Осознанно используем отличные от общепринятых обозначения для упрощения формулировок. Это статья для того, чтобы ухватить основную суть. Тогда дальше будет проще.

В первой части определим пространство на основе правил внешнего произведения и сложения объектов. Во второй добавим пространству метрические свойства. В целом пройдем путь от внешнего произведения до представления произвольных графов в виде алгебраического выражения. По дороге познакомимся с основными идеями и инструментами внешней алгебры.

Внешнее произведение

Суть внешней алгебры в том, что объекты можно умножать. Если вас это не впечатлило, то еще раз - умножать можно любые объекты, а не только числа. Можно умножать людей, города, компьютеры, бухгалтерские счета и все остальное, что подходит под понятие объекта. Такое произведение объектов называется "внешним умножением". Это исторически сложившийся термин для того, чтобы отличать внешнее произведение от внутреннего, которым обычно обозначают скалярное произведение.

Обычно внешнее произведение математики обозначают клином (wedge). Но этот знак неудобен. Во-первых, его нет на клавиатуре. Во-вторых, никакого другого умножения, кроме внешнего, для произвольных объектов не существует. Поэтому будем обозначать внешнее произведение звездочкой. Вот оно, умножение элементана элемент: .

Выглядит знакомо, да? Но в отличие от привычного произведения чисел внешнее произведение антикоммутативно - проще говоря, меняет знак при перестановке множителей. Вот так:

Это важное свойство, которое является ключевым для внешней алгебры. Из него в частности следует, что внешнее произведение элемента на самого себя может быть только нулем - объектом без знака: .

Какой смысл несет в себе "внешнее произведение". По простому - это ничто иное, как объединение объектов в список. Поэтому, когда элементов много, то их удобно обозначить списком. Такой упорядоченный список выделим квадратными скобками:. При этом надо помнить про наличие знака у списка - при перестановке соседних элементов знак списка меняется на противоположный: . Ну и как следствие - в таком списке не может быть одинаковых элементов.

Список с такими свойствами будем называть симплексом. Симплекс из двух элементов - отрезок, из трех - треугольник, и т. д. (Только надо иметь ввиду, что это топологические отрезки и треугольники. У них нет длин, углов и прочих метрических параметров.). Количество элементов симплекса задает его порядок (грейд). Математики чаще используют понятие мерности. Размерность симплекса на 1 меньше его порядка. То есть отрезок является одномерным.

Симплексы можно умножать друг на друга - это будет эквивалентно объединению двух списков: . Но при наличии в множителях одинаковых элементов результатом объединения будет пустой список - нуль: .

Ну и еще одно полезное правило. При перестановке перемножаемых симплексов местами знак меняется на противоположный, если произведение порядков симплексов нечетное:

Здесь нижние индексы обозначают порядок симплексов.

Обратные элементы

В нашей алгебре не обойтись без понятия единицы. Единица - это такой элемент, при умножении на который с любой стороны симплекс остается без изменений: . В свою очередь наличие единицы позволяет расширить множество элементов, введя понятие обратных. Кратко обратные элементы именуют коэлементами. При умножении на обратный элемент обращается в единицу. Поскольку у нас не обычное умножение, а внешнее, то важно относительное положение множителей - при перемене мест элемента и обратного ему единица становится отрицательной. Для удобства (связанного с понятием граничного оператора) постулируем, что если обратный элемент расположен слева, то результатом произведения будет 1, а если справа, то -1. Это выглядит поначалу немного непривычно, но в целом окупается:

Здесь перед коэлементами стоит префикс в виде косой черты /. Если обратный элемент умножается на другой элемент, то результатом будет пустой симплекс - ноль: .

Коэлемент можно трактовать как отсутствие элемента. Это дырка в множестве. Но интересно, что с коэлементами можно обращаться так же как с обычными. Произведение коэлементов образует обратный симплекс (косимплекс). Для заданного симплекса можно определить обратный. Постулируем, что при умножении обратного слева на исходный должны получить 1 независимо от порядка симплекса: . Отсюда следует правило расположения элементов в обратном симплексе - в нем порядок элементов меняется на обратный. Таким образом если, то.

Если симплекс умножить на обратный справа, то результат зависит от четности порядка симплекса:

Если симплекс умножается на косимплекс, то взаимно обратные элементы должны сокращаться. Для того, чтобы правильно учесть знак необходимо элемент и обратный ему поставить рядом и выполнить сокращение с учетом их положения. Например: .

Если перемножаемые симплекс и косимплекс содержат элементы, которых нет в другом, то результатом произведения будет ноль: .

Отметим, что симплекса, образованного одновременно обычными и обратными элементами - не существует. Симплексы однородны по составу - либо симплекс полностью состоит из обычных элементов, либо из обратных. Данное свойство вытекает из правил перемножения симплексов. В этом смысле множества обычных элементов и коэлементов принадлежат разным пространствам.

Линейные комбинации и цепи

Элементы и симплексы можно не только умножать, но и складывать, образуя линейные комбинации. Перед каждым симплексом в комбинации может быть скалярный множитель (число). Пример линейной комбинации симплексов 2-го порядка:

.

Линейные комбинации тоже можно интерпретировать как список элементов (слагаемых). Однако в отличие от симплекса в линейных комбинациях допускается наличие произвольного количества одинаковых элементов. Коэффициенты линейной комбинации отражают кратность элементов списка, при этом допускаются и отрицательные кратности. Правила раскрытия двух видов списков отражаются законом дистрибутивности:

Но надо помнить, что умножение здесь внешнее (антикоммутативное). Поэтому некоторые привычные формулы выглядят иначе. Например, внезапно.

Линейную комбинацию симплексов одного порядка в топологии называют также цепью. Как правило, коэффициенты слагаемых цепи целочисленные. Поэтому в общем случае цепи являются подмножеством произвольных линейных комбинаций симплексов. Порядок цепи совпадает с порядком симплексов, из которых она состоит.

Линейную комбинацию можно рассматривать как разложение некоего объекта того же порядка по базисным. Например, если у нас есть два объектаи, то можно определить объект как их линейную комбинацию:

Полученный объект является зависимым, или производным. Отметим, что умножение производного объекта на симплекс его базиса, дает ноль:. То есть зависимые объекты не создают нового пространства. Ну или по другому - размерность пространства определяется количеством независимых элементов.

Коэффициенты разложения элемента по базисным могут быть определены через умножение на коэлементы базиса:

Получается, что внешнее произведение элементов и коэлементов является скалярным (в том смысле, что результат является скаляром). Но между самими элементами скалярное произведение не определено.

Аннулятор и граница

Мы определили симплексы как произведение элементов, определили обратные элементы и обратные симплексы, ввели понятие линейной комбинации симплексов. Пора разобраться с понятием вектор. Часто вектор появляется в учебниках как "черт из табакерки" - то есть явочным порядком. Но постулируя вектор как независимое понятие, мы препятствуем осмыслению его обобщения, создаем искусственный барьер в понимании "реальной картины мира". В нашей алгебре первично понятие объекта (элемента). Вектор - производное понятие, и сейчас мы его "произведем".

Вначале нам понадобится еще одно фундаментальное понятие, которое имеет разные названия, в зависимости от контекста в котором употребляется. Здесь для него используем абстрактный термин - аннулятор, хотя пока и непонятно, чего он там обнуляет. Пусть имеется некое конечное множество элементов, например, . Тогда аннулятором для данного множества является сумма обратных элементов данного множества:

Согласно определению аннулятор принадлежит копространству (пространству обратных элементов), поэтому для его обозначения используем косую черту. Поскольку у каждого симплекса есть множество образующих его элементов, то любому симплексу можно сопоставить аннулятор. При этом от знака симплекса аннулятор не зависит.

Аннулятор позволяет определить граничный оператор над симплексом как внешнее умножение аннулятора на симплекс. Результатом действия является граница. Вот она, граница симплекса:

Границы настолько важны, что не пожалеем для их обозначения отдельных скобок:

Аннулятор множества является также аннулятором всех его подмножеств. Поэтому граница симплекса может быть образована умножением не только на его аннулятор, но и на любой аннулятор надмножества. Пример:

Граница (симплекса) есть цепь - линейная комбинация симплексов. Порядок границы на 1 меньше порядка образующего ее симплекса. В частности, вектор - это граница 1-порядка, образованная отрезком (симплексом 2-го порядка):

Вектор 2-го порядка называют бивектором, 3-го - тривектором и т.д. Граница произвольного порядка может быть названа мульти- или поливектором.

Действие граничного оператора может быть отменено. Существует элемент, умножая на который границу симплекса, можно восстановить исходный симплекс. Данный элемент называется центроидом множества (или барицентром). Центроид - это среднее суммы элементов:

Здесь круглые скобки - это не обозначение границы, а группировка элементов (обычно смысл скобок понятен из контекста). Проверим действие центроида:

Умножение границы на центроид собирает несколько слагаемых в одно.

Основное свойство границ

Границы - это не просто цепи, фактически границы представляют собой новый тип данных со своими особыми свойствами. Главное из них - двойная граница равна нулю.

В традиционных учебниках граничный оператор вводят явочным порядком, и в этом случае приходится доказывать тот факт, что двойной граничный оператор дает ноль. Но в нашем изложении это очевидно ввиду того, что граничный оператор определен как умножение на аннулятор. Повторное умножение на тот же элемент дает ноль в соответствии со свойствами внешнего произведения.

Данная формула раскрывает смысл термина "аннулятор" - при действии на границу аннулятор ее обнуляет. Раскрывая границу как линейную комбинацию симплексов и умножая каждый симплекс на аннулятор, получаем тождества границ:

Тождества границ играют ключевую роль в различных доказательствах и выводах, касающихся свойств границ. Например, из них вытекает полезные выражения исключения вершиныиз линейной комбинации границ:

Общий элементв правой части тождеств можно также интерпретировать как центр координат. На этом свойстве основано определение векторного пространства с общим центром, который всегда можно исключить. при выражении других границ пространства.

Становится понятно также, что двум различным цепям может соответствовать одна и та же граница при условии, что разность данных цепей является границей. Соответственно и восстановление цепи по границе (умножением на центроид) выполняется с точностью до произвольной границы.

Произведение границ

Обратимся к произведению границ. Произведение двух границ тоже является границей, но есть нюансы. Если перемножаемые границы имеют более одного общего элемента, то их произведение равно нулю. Это следствие свойств внешнего произведения. Пример:

Если границы имеют один общий элемент, то при умножении они сливаются в одну (компоненту) - это правило слияния границ. Пример слияния двух векторов в 2-границу (бивектор):

Если же перемножаемые границы не имеют общих элементов, то границы не сливаются. Получаем границу, состоящую из нескольких компонент связности. Пример такой границы, содержащей 4 элемента:. Поскольку под поливектором обычно понимают границу с одной компонентой связности, то строго говоря границы и поливекторы - это не одно и то же. Под поливектором будем понимать всегда границу из одной компоненты.

Итак, порядок границы зависит не только от количества образующих ее элементов , но и от количества ее компонент . Порядок границы равен 2, несмотря на то, что она содержит 4 элемента. Для получения порядка границы надо из количества элементов вычесть количество компонент: .

Кроме того, одна и та же граница может быть образована произведением разных границ меньшего порядка. Например, граница может быть образована тремя разными парами векторов: . То есть произведение границ с общим элементом уничтожает информацию о том, какие именно границы умножались - границы сливаются в одну.

Для тех, кому интересны подробности, откуда все это следует

Немного линейной алгебры...

Пространство элементов, с которым мы тут возимся, принято называть аффинным. Это пространство, в котором есть элементы и их линейные комбинации, но нет метрики.

Насчет метрики следует уточнить. В нашем пространстве не определено скалярное произведение между элементами (и между границами тоже). Поэтому нет возможности определить, например, угол между векторами или сравнить длину (норму) двух произвольных векторов. Но. Из этого не следует, что в аффинном пространстве вообще невозможно ничего сравнивать. Мы вполне можем сравнить длину двух векторов, если они лежат на одной прямой. Мы можем сравнить площади двух бивекторов, если они лежат в одной плоскости и т.д. То есть полноценной метрики в аффинном пространстве нет, но есть полуметрика, которой вполне можно пользоваться. Полуметрика является следствием наличия скалярного произведения между элементами и коэлементами. То есть линейного разложения элементов через другие, базисные.

Рассмотрим пространство, образованное тремя элементами, среди которых выделим центр - общий элемент. Границей пространства будет бивектор базиса. Пусть теперь в данном пространстве есть три элементас известными координатами относительно базисных элементов. Задача состоит в том, чтобы выразить бивекторчерез базисный.

Вначале выпишем координаты элементов. Учтем, что сумма коэффициентов разложения элемента по базисным должна быть равна единице - это следствие того, что граница любого элемента пространства должна быть равна 1: . Такие координаты называются барицентрическими. Тогда для базиса из 3-х элементов две координаты являются независимыми, а третья - выражается через них:

Данная формула может быть представлена как координаты вектора :

Аналогичным образом можно найти координаты векторови. Перемножая векторы, можно выразить координаты бивекторов через базисный бивектор:

Для нахождения искомого бивекторавоспользуемся тождеством границ из предыдущего раздела: . Подставляя в него координаты бивекторов, получаем итоговый ответ:

Значение скалярного коэффициента здесь как раз и будет отношением площадей искомого и базового бивекторов. Отметим, что коэффициент может быть и отрицательным, поскольку у бивекторов есть ориентация.

Аффинные координаты и площади

Коэффициент может быть также выражен как детерминант матрицы: . Значения матрицы координатравны произведению элементов и базисных коэлементов (за исключением центра координат):

Для вычисления относительного объема в матрицу добавляется дополнительная строка и колонка, соответствующие новому измерению.

Умение различать ситуации, где пространство является аффинным, является полезным навыком при анализе данных. Пусть, например, задано множество людей, для которых известны рост и вес. Данные свойства образуют два вектора аффинного пространства. Как показано выше, в таком пространстве можно сравнивать людей отдельно по росту или весу, но нет возможности оценить близость людей одновременно по "росто-весу", поскольку нет связи между данными свойствами, нет метрики. Но ничто не мешает сравнивать по "росто-весу" тройки людей. Координаты этих троек (вычисленные указанным выше способом) пропорциональны их относительной площади и не зависят от скалярного произведения свойств (угла между базисными векторами).

... и топологии

Про топологию говорят, что это геометрия без измерений. В том смысле, что конкретные координаты элементов топологам неинтересны. Поэтому коэффициенты топологических цепей всегда равны +-1. Алгебраические выражения границ симплекса можно интерпретировать топологически. В качестве примера приведем разрезание (топологического) квадрата с вершинами на два треугольника. Треугольники в данном случае должны быть ориентированы, то есть иметь знак. Тогда квадрат можно представить как сумму (склейку) треугольников:. Применив к данной цепи граничный оператор, получим цепь из 4-х 2-симплексов - это граница квадрата:

Склейка симплексов

При сложении 2-границ общая сторона треугольников сократилась. В общем случае, можно продолжать склейку треугольников, получая произвольные топологические многогранники. Кажется, что можно любую поверхность представить как сумму треугольников, но на самом деле нет. При покрытии треугольниками поверхности ленты Мёбиуса не удается сократить внутренние границы!

Мы определили границу симплексакак результат действия граничного оператора (умножение аннулятора) на некий симплекс. Повторное взятие границы, как уже отмечалось дает ноль:

Но вообще говоря, возможны и другие цепи (линейные комбинации симплексов), граница которых нулевая. Цепи с нулевой границей называют циклами. Инвариант циклов:

Циклы - это более общее подмножество цепей, чем границы. В общем случае существуют циклы, которые не являются границами какого-либо симплекса. Их называют гомологиями:

Говоря про циклы, снова оговоримся - это топологические циклы. Так же как в топологическом треугольнике нет величины сторон и углов, так и в топологическом цикле нет величины связи между элементами цикла.

Топология - огромный раздел современной математики. Тут мы лишь показали, как порождаются и связываются направления математики через одну простую операцию - внешнее умножение.

Коцепи и дуальность

Для заданного конечного множества независимых элементов существует симплекс предельного порядка, определяемый как произведение всех элементов. Граница данного симплекса называется предельной границей пространства - она имеет максимальный порядок из всех возможных границ на данном множестве. Предельная граница для множества 4-х элементов : .

Предельная граница множества всегда связна (имеет только одну компоненту). Умножение предельной границы на коэлементы понижает ее порядок, но оставляет границу связной: . Умножение предельной границы на сумму коэлементов порождает границы, состоящие из компонент. Например,

Здесь мы видим коцепи 1-го порядка - это линейные комбинации коэлементов. Встречаются также коцепи более высокого порядка. Например, граница из трех компонент может быть получена умножением предельной границы на аннуляторы двух произвольных компонент:

Здесь- предельная граница 6 элементов. Коцепь 2-го порядка:

Видим, что разным коцепям может соответствовать одна и та же граница. Из данных соотношений следует, что границуна конечном множестве элементов можно задать через коцепь. Умножая коцепь на предельную границу, переходим из копространства в обычное:

Преобразование коцепей в границы называется дуальным преобразованием.

Дуальное преобразование и звездочка Ходжа - это не одно и тоже!

Можно определить и обратное дуальное преобразование - от границ (цепей) к коцепям. Пусть дана некая граница (в общем случае произвольная цепь). Надо построить дуальную ей коцепь для заданного пространства (симплекса) с предельной границей .

Алгоритм построения может быть таким. Для цепи определяем центроид (средняя сумма элементов, образующих цепь). "Интегрируем" цепь умножением слева на центроид. Переводим полученный "интеграл" из пространства в копространство умножением на косимплекс пространства. Косимплекс пространства однозначно определяется предельной границей. Полученная коцепь и будет искомой:

В данной формуле круглые скобки обозначают порядок операций.

На этом завершаем. Надеюсь, что общее представление о том, что такое внешняя алгебра, читатели получили. Самое странное, что все эти "игры с абстрактными символами" отражают свойства вполне реального окружающего мира. В следующей статье рассмотрим пространства со скалярным произведением между элементами.

Трансформеры за последние несколько лет штурмом захватили мир NLP, а сегодня они с успехом применяются в выходящих за рамки NLP приложениях. Они обладают такими возможностями благодаря модулю внимания, который схватывает отношения между всеми словами последовательностей. Но самый важный вопрос как именно трансформеры делают это? Попытаемся ответить и понять, почему трансформеры способны выполнять такие вычисления. Итак, цель статьи, чуть сокращённым переводом которой мы делимся к старту курса о машинном и глубоком обучении, разобраться не только с тем, как что-то работает, но и почему работает так. Чтобы понять, что движет трансформерами, мы должны сосредоточиться на модуле внимания. Начнём с входных данных и посмотрим, как они обрабатываются.

---

Как входная последовательность попадает в модуль внимания

Модуль внимания присутствует в каждом энкодере внутри стека каждого энкодера, а также внутри стека каждого декодера. Сначала внимательно посмотрим на энкодер.

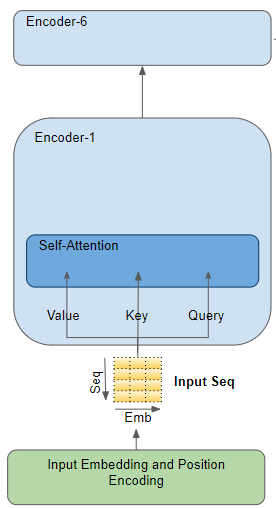Модуль внимания в энкодере

Для примера предположим, что мы работаем над задачей перевода с английского на испанский, где исходная последовательность слов The ball is blue, а целевая последовательность La bola es azul.

Исходная последовательность сначала проходит через слой векторного представления и позиционного кодирования, генерирующего векторы векторного представления для каждого слова последовательности. Векторное представление передаётся в энкодер, где вначале попадает в модуль внимания.

Внутри модуля внимания последовательность векторного представления проходит через три линейных слоя, создающих три отдельные матрицы запроса (Query), ключа (Key) и значения (Value). Именно эти три матрицы используются для вычисления оценки внимания [прим. перев. оценка определяет, сколько внимания нужно уделить другим частям входного предложения, когда мы кодируем слово в определённой позиции]. Важно помнить, что каждая "строка" этих матриц соответствует одному слову исходной последовательности.

Поток исходной последовательности

Каждая входная строка это слово из последовательности

Чтобы понять, что происходит с модулем внимания, мы начнём с отдельных слов исходной последовательности, проследив их путь через трансформер. Если конкретнее, мы хотим сосредоточиться на происходящем внутри модуля внимания. Это поможет нам чётко увидеть, как каждое слово в исходной и целевой последовательностях взаимодействует с другими словами этих последовательностей.

Пока вы разбираетесь с этим объяснением, сосредоточьтесь на том, какие операции выполняются с каждым словом и как каждый вектор отображается на исходное входное слово. Не нужно думать о множестве других деталей, таких как формы матриц, особенности арифметических вычислений, множественное внимание и так далее, если эти детали не относятся напрямую к тому, куда направляется каждое слово. Итак, чтобы упростить объяснение и визуализацию, давайте проигнорируем размерность векторного представления и будем отслеживать только строки для каждого слова.

Расположение каждого слова в исходной последовательности

Каждое слово проходит серию обучаемых преобразований (трансформаций)

Каждая такая строка была сгенерирована из соответствующего исходного слова посредством серии трансформаций векторного представления, позиционного кодирования и линейного слоя. Все эти трансформации возможно обучить; это означает, что используемые в этих операциях веса не определены заранее, а изучаются моделью таким образом, чтобы они давали желаемые выходные прогнозы.

Линейные веса и веса векторного представления обучены

Ключевой вопрос заключается в том, как трансформер определяет, какой набор весов даст ему наилучшие результаты? Держите этот момент в памяти мы вернёмся к нему немного позже.

Оценка внимания это скалярное произведение матрицы ключа и матрицы запроса слов

Модуль внимания выполняет несколько шагов, но здесь мы сосредоточимся только на линейном слое и на оценке внимания.

Многоголовое вниманиеРасчёт оценки внимания

Как видно из формулы, первый шаг в рамках модуля внимания умножение матрицы, то есть скалярное произведение между матрицей Query (Q) и транспонированием матрицы ключа Key (K). Посмотрите, что происходит с каждым словом. Итог промежуточная матрица (назовём её факторной матрицей [матрицей множителей]), где каждая ячейка это результат матричного умножения двух слов.

Скалярное произведение матрицы запроса и матрицы ключа

Например, каждый столбец в четвёртой строке соответствует скалярному произведению между четвёртым словом запроса и каждым ключевым словом.

Скалярное произведение между матрицами запроса и ключа

Оценка внимания скалярное произведение между запросом-ключом и значением слов

Следующим шагом является матричное умножение между этой промежуточной матрицей множителей и матрицей значений (V), чтобы получить оценку внимания, который выводится модулем внимания. Здесь мы можем видеть, что четвёртая строка соответствует четвёртой матрице слов запроса, умноженной на все остальные ключевые слова и значения.

Скалярное произведение между матрицами ключа запроса и значения

Получается вектор оценки внимания (Z), который выводится модулем внимания. Выходной результат можно представить следующим образом: для каждого слова это закодированное значение каждого слова из матрицы Значение, взвешенное матрицей множителей. Матрица множителей представляет собой точечное произведение значения запроса для данного конкретного слова и значения ключа для всех слов.

Оценка внимания это взвешенная сумма значения слов

Какова роль слов запроса, ключа и значения?

Слово запроса это слово, для которого мы рассчитываем внимание. В свою очередь слово ключа и значения это слово, на которое мы обращаем внимание, то есть определяем, насколько это слово соответствует слову запроса.

Оценка внимания для слова blue обращает внимание на каждое слово

Например, для предложения The ball is blue строка для слова blue будет содержать оценку внимания для слова blue с каждым вторым словом. Здесь blue это слово запроса, а другие слова ключ/значение. Выполняются и другие операции, такие как деление и softmax, но мы можем проигнорировать их в этой статье. Они просто изменяют числовые значения в матрицах, но не влияют на положение каждой строки слов в ней. Они также не предполагают никаких взаимодействий между словами.

Скалярное произведение сообщает нам о сходстве слов

Итак, мы увидели, что оценка внимания отражает некоторое взаимодействие между определённым словом и каждым другим словом в предложении путём скалярного произведения с последующим их сложением. Но как матрица умножения помогает трансформеру определять релевантность между двумя словами?

Чтобы понять это, вспомните, что строки запроса, ключа и значения на самом деле являются векторами с размерностью векторного представления. Давайте посмотрим, как умножаются матрицы между этими векторами.

Каждая ячейка представляет собой скалярное произведение двух векторов слов

Для получения скалярного произведения двух векторов мы умножаем пары чисел, а затем суммируем их.

• Если два парных числа (например, a и d выше) оба положительны или оба отрицательны, произведение положительно. Произведение увеличит итоговую сумму.

• Если одно число положительное, а другое отрицательное, произведение будет отрицательным. Произведение уменьшит итоговую сумму.

• Если произведение положительное, то, чем больше два числа, тем больше их вклад в окончательную сумму.

Это означает, что, если знаки соответствующих чисел в двух векторах выровнены, итоговая сумма будет больше.

Как трансформер изучает релевантность между словами?

Скалярное произведение также применимо к оценке внимания. Если векторы для двух слов более выровнены, оценка внимания будет выше. Итак, какого поведения мы хотим от трансформера? Мы хотим, чтобы оценка внимания была высокой для двух релевантных друг другу слов в предложении. И мы хотим, чтобы оценка двух слов, не связанных друг с другом, была низкой.

Например, в предложении The black cat drank the milk слово milk очень релевантно к drank, возможно, немного менее релевантно для cat, и нерелевантно к black. Мы хотим, чтобы milk и drink давали высокую оценку внимания, чтобы milk и cat давали немного более низкую оценку, а для milk и black незначительную. Мы хотим, чтобы модель научилась воспроизводить этот результат. Чтобы достичь воспроизводимости, векторы слов milk и drank должны быть выровнены. Векторы milk и cat несколько разойдутся. А для milk и black они будут совершенно разными.

Давайте вернёмся к вопросу, который мы откладывали: как трансформер определяет, какой набор весов даст ему наилучшие результаты? Векторы слов генерируются на основе векторного представления слов и весов линейных слоёв. Следовательно, трансформер может изучить эти векторные представления, линейные веса и так далее, чтобы создать векторы слов, как требуется выше.

Другими словами, он будет изучать эти векторные представления и веса таким образом, что если два слова в предложении релевантны друг другу, то их векторы слов будут выровнены, следовательно, получат более высокe. оценку внимания. Для слов, которые не имеют отношения друг к другу, их векторы не будут выровнены и оценка внимания будет ниже.

Следовательно, векторные представления слов milk и drank будут очень согласованными и обеспечат высокую оценку внимания. Они будут несколько отличаться для milk и cat, производить немного более низкую оценку и будут совершенно разными в случае milk и black: оценка внимания будет низкой вот лежащий в основе модуля внимания принцип.

Итак, как же работает трансформер?

Скалярное произведение между запросом и ключом вычисляет релевантность между каждой парой слов. Эта релевантность затем используется как множитель для вычисления взвешенной суммы всех значений слов. Эта взвешенная сумма выводится как оценка внимания. Трансформер изучает векторные представления и т. д. таким образом, что релевантные друг другу слова были более согласованы.

В этом кроется одна из причин введения трёх линейных слоёв и создания трёх версий входной последовательности: для запроса, ключа и значения. Такой подход даёт модулю внимания ещё несколько параметров, которые он может изучить, чтобы подстроить процесс создания векторов слов.

Самовнимание энкодера в трансформере

Внимание используется в трансформере в трёх местах:

• Самовнимание в энкодере исходная последовательность обращает внимание на себя.

• Самовнимание в декодере целевая последовательность обращает внимание на себя.

• Энкодер-декодер-внимание в декодере целевая последовательность обращает внимание на исходную последовательность.

Внимание в Трансформере

В самовнимании энкодера мы вычисляем релевантность каждого слова в исходном предложении каждому другому слову в исходном предложении. Это происходит во всех энкодерах стека.

Декодер самовнимания в трансформере

Большая часть того, что мы только что видели в энкодере самовнимания, применима и к вниманию в декодере, но с некоторыми существенными отличиями.

Внимание в декодере

В декодере самовнимания мы вычисляем релевантность каждого слова в целевом предложении каждому другому слову в целевом предложении.

Самовнимание декодера

Энкодер-декодер модуля внимания в трансформере

В энкодере-декодере запрос получается из целевого предложения, а ключ/значение из исходного предложения. Таким образом, он вычисляет релевантность каждого слова в целевом предложении каждому слову в исходном предложении.

Энкодер-декодер Внимания

Заключение

Надеюсь, статья дала вам хорошее представление об элегантности архитектуры трансформера. Прочтите также другие статьи о трансформере из моей серии, чтобы лучше представлять, почему сегодня трансформер это предпочтительная архитектура многих приложений глубокого обучения.

Здесь мы видим, что за сложными идеями скрываются простые решения. Более того, есть ощутимая вероятность того, что вскоре понимание внутренних механизмов глубокого обучения станет второй грамотностью, как сегодня второй грамотностью стало знание ПК в целом и если вы хотите углубиться в область глубокого и машинного обучения, получить полное представление о современном ИИ, вы можете присмотреться к нашему курсу Machine Learning иDeep Learning, партнёром которого является компания NVIDIA.

Узнайте, как прокачаться и в других специальностях или освоить их с нуля:

• Профессия Data Scientist

• Профессия Data Analyst

• Курс по Data Engineering

Другие профессии и курсы