Геймплей симулятора транспортного средства управление движением транспортного средства в пространстве с некоторым количеством степеней свободы. Действия игрока изменяют вектор мгновенного состояния системы в желаемом или не совсем желаемом направлении. Игра вряд ли сможет быть интересной, если объект слабо приспособлен к управлению игроком.
Приспособленность технической системы к управлению человеком (управляемость) довольно сложная и многогранная характеристика. Математической моделью поведения управляемого объекта занимается теория автоматического управления (ТАУ). Модели, принятые в ТАУ, могут описывать и поведение игрока человека-оператора, и поведение системы человек-машина.
Стоит отметить, что создаваемые модели человека всегда актуальны для ограниченного набора условий. По этой причине решение практических задач в области управляемости часто выходит за рамки ТАУ.
Управляемость машины относится к ее эргономическим свойствам, теряющим смысл в отрыве от контекста деятельности человека. Под катом представлен подход к настройке модели симулятора, основанный на экспериментальном исследовании процесса игры.
Для симуляторов, претендующих на точное моделирование существующих систем, важно сходство с прототипом, какой бы плохой ни была его управляемость. Оптимизация же характеристик актуальна для игр, в которых нет заданной модели, например, симуляторов фантастических объектов.
Оставляя в стороне задачу имитации реального объекта с заданным набором характеристик, отметим, что симулятор наверняка не проиграет от наличия субъективно определяемой физичности. Другими словами, даже объект, не существующий в природе, может соответствовать или не соответствовать ожиданиям игрока относительно его (объекта) поведения. Фактор естественности поведения объекта должен быть принят во внимание.
Постановка задачи
Для симулятора необходимо настроить коэффициенты математической модели транспортного средства так, чтобы обеспечивалась его наилучшая управляемость. Оптимизация должна выполняться на основе экспериментальных данных. Желательно получить модель, кажущуюся игроку естественной.
Описание системы
В экспериментах будем использовать симулятор с 3D-графикой.
Сложность математической модели реального транспортного средства ограничивается лишь принятым уровнем абстракции и грубостью используемых допущений. Сложность модели в решаемой здесь задаче определяется рациональным уровнем естественности игры.
Ниже будут применены следующие упрощения:
1. Направление движения объекта принимается совпадающим с его продольной осью.
2. Вращательное движение объекта может рассматриваться как сумма независимых составляющих вращательных движений относительно трех осей связанной с объектом системы координат (ССК).
3. Угловое ускорение в отдельном канале управления (вокруг отдельной оси ССК) определяется линейной комбинацией текущих значений управляющего действия и угловой скорости в этом канале.
Приемлемость первого упрощения в моделировании реальных объектов определяется свойствами системы и решаемой задачей. Например, общеизвестным свойством дротиков является их способность лететь после броска острием вперед. Этой простой модели достаточно, чтобы получить полезный вывод: не стоит подбрасывать дротик вверх над собой.

Но если необходима точная модель для определения последствий контакта дротика с целью, то следует учитывать, что в полете его вектор скорости составляет некоторый угол с продольной осью.
Постоянство направления вектора скорости в системе координат объекта соответствует биомеханике ходьбы: человеку проще всего идти, сохраняя состояние лицом вперед. Движение в непривычных направлениях, наоборот, ухудшает игроку обзор и требует от него дополнительных умственных усилий.
П. 2 устанавливает взаимную изолированность каналов управления, прикрепленных к осям ССК.

Оси ССК: продольная (X) направлена от хвоста к носу объекта, вертикальная (Y) направлена в плоскости симметрии объекта вверх при его начальном положении, боковая (Z) направлена перпендикулярно первым двум вправо. Соответственно, вращение вокруг оси X боковой канал, вокруг оси Y путевой канал, вокруг оси Z продольный канал.
В соответствии с п. 2 принятых упрощений между каналами управления объектом отсутствуют перекрестные связи. Реальные системы всегда соответствуют такой модели с некоторой ошибкой, обусловленной, например, наличием гироскопических моментов. Отсутствие перекрестных связей является преимуществом с точки зрения игрока.
П. 3 устанавливает наличие только двух крутящих моментов в каждом канале управления:
- управляющий момент, пропорциональный сигналу от управления игрока;
- момент демпфирования, пропорциональный текущей угловой скорости.
Дифференциальное уравнение вращения вокруг оси i выглядит следующим образом:

Здесь омега угловая скорость вращения, t время, x управляющий сигнал, а коэффициенты в правой части уравнения частные производные углового ускорения по управляющему сигналу и угловой скорости.
Первый коэффициент будем называть коэффициентом эффективности управления, второй коэффициентом демпфирования.
Угловое ускорение измеряется в [рад/с2], угловая скорость в [рад/с]. Управляющий сигнал обычно измеряется в единицах перемещения рычагов или усилий на них, реже в единицах положения промежуточных элементов системы управления, но для управления с клавиатуры примем эту величину безразмерной. Размерность коэффициента демпфирования [1/c], а коэффициента эффективности управления [рад/с2] с учетом принятой размерности управляющего сигнала.
- переходной функции;
- амплитудной частотной характеристики (АЧХ);
- фазовой частотной характеристики (ФЧХ).
Входной сигнал звена в уравнении (1) x, выходной угловая скорость. В стандартном виде уравнение апериодического звена первого порядка записывается следующим образом:
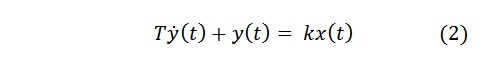
Здесь х(t) входной сигнал, y(t) выходной сигнал, точка над y производная по времени, k коэффициент усиления звена, T постоянная времени, характеризующая инерционность звена.
Сопоставление уравнений (1) и (2) приводит к следующим соотношениям:


Рассмотрим переходную функцию (переходный процесс) системы, описывающую ее реакцию на ступенчатый входной сигнал в виде функции Хевисайда. Значение такого сигнала равно нулю для отрицательных значений аргумента (времени) и единице для неотрицательных. Переходная функция зависимость от времени выходного сигнала.

Переходный процесс апериодического звена первого порядка описывается следующим уравнением:

Уравнение демонстрирует роли коэффициентов:
- k соответствует установившемуся значению выходного сигнала;
- T оправдывает название постоянная времени, например, за время t = 3T выходной сигнал достигает уровня 0,95k.
Переходному процессу можно дать следующее неформальное описание:
1. В начальный момент времени ускорение достигает максимального уровня (равно коэффициенту эффективности управления), скорость не успела получить приращения, и демпфирование на систему не влияет.
2. Скорость растет, рост скорости влечет за собой рост влияния демпфирования, суммарное ускорение снижается.
3. Демпфирование асимптотически приближается по своему уровню к управляющему действию, соответственно, ускорение становится пренебрежимо малым, а скорость приближается к значению коэффициента k.

Таким образом, ступенчатый входной сигнал управления приводит к плавному нарастанию угловой скорости до некоторого уровня. Достигаемое значение и плавность нарастания зависят от величин k и T.
Частотные характеристики описывают реакцию системы на входной сигнал в виде гармонических колебаний. АЧХ и ФЧХ являются функциями частоты входного сигнала.
При управлении игрой с клавиатуры входной сигнал звена является дискретным и имеет всего три возможных значения. Например, для продольного канала это следующие варианты: нажата кнопка подъема носа единица, ни одна из кнопок не нажата ноль, нажата кнопка опускания носа минус единица. Входной сигнал кусочно-постоянная функция, которая на первый взгляд не может иметь много общего с синусоидой.
Тем не менее, действия игрока могут рассматриваться как подобие широтно-импульсной модуляции, при которой промежуточные уровни сигнала подменяются суммарными длительностями импульсов на интервале времени. Рассмотрение частотных характеристик вполне способно улучшить понимание взаимодействия игрока и симулятора.
Если входной сигнал имеет форму гармонических колебаний, то с изменением их частоты у выходного сигнала изменится не только частота колебаний, но и их амплитуда. Изменится и сдвиг фазы между колебаниями входного и выходного сигналов.


При заданной частоте входного сигнала значение АЧХ соответствует амплитуде установившихся колебаний выходного сигнала, отнесенной к амплитуде колебаний входного сигнала. Значение ФЧХ равно сдвигу фазы колебаний выходного сигнала относительно колебаний входного.
Значение АЧХ апериодического звена первого порядка при отсутствии колебаний (значение частоты равно нулю) соответствует значению k. Это свойство легко выводится из рассмотренной выше переходной характеристики.

Снижение амплитуды выходного сигнала с ростом частоты входного определяется значением T (или значением коэффициента демпфирования). Звено с меньшим значением T лучше пропускает сигнал.
ФЧХ определяется только значением коэффициента демпфирования (или T).

Фазовое отставание растет с увеличением частоты, асимптотически приближаясь к уровню минус ПИ/2. Меньшее фазовое отставание при равных частотах входа соответствует моделям с меньшими значениями T.
Частотные характеристики наглядно показывают роли коэффициента демпфирования и постоянной времени звена: слабое демпфирование (большие значения T) ведет к потере амплитуды выходного сигнала и росту его фазового отставания.
Условия эксперимента и критерии качества модели
Лучшая управляемость объекта должна обеспечивать более эффективное решение задачи игроком. Но разные задачи требуют разной управляемости: точное выдерживание параметров заданного режима движения существенно отличается от интенсивного маневрирования.
Поиск универсальной модели для любых задач неизбежно связан с компромиссом. Условия проводимого эксперимента определяют субъективное смещение баланса в пользу тех или иных задач. Тем не менее, конкретные условия игры должны быть выбраны.
Для исследования будем использовать задачу посещения управляемым объектом максимального количества локаций из числа заданных за ограниченное время. Эффективное решение этой задачи требует интенсивного маневрирования.
Управление аппаратом будет осуществляться с ограничениями по углам крена и тангажа (60 градусов в обоих направлениях для обоих углов): выход за ограничения ведет к аварии. Также к аварии ведет столкновение с горизонтальной поверхностью, расположенной над объектом. Эта часть условий отвечает за составляющую выдерживания параметров в задаче игрока.
Значение модуля линейной скорости объекта принимается постоянным. Это означает, что управление акселератором, как и неравномерность сопротивления среды, в симуляторе отсутствует.
Показатель эффективности работы игрока количество локаций, посещенных до окончания времени (60 секунд) или до аварии. Чем больше посещено локаций, тем более качественной считается модель. С каждой моделью (набором значений коэффициентов) предусмотрено три прохождения игры с принятием в зачет медианного результата.
При планировании экспериментов важно минимизировать влияние фактора обучения. Для этого был определен порядок экспериментов, при котором каждая модель запускается в первой, второй и третьей третях исследования:
A, B, C N, O,
A, B, C N, O,
A, B, C N, O.
Каждому экспериментальному прохождению предшествовала одна тренировочная игра с соответствующей моделью.
Симулятор
Экспериментировать с коэффициентами модели самостоятельно можно здесь.
Управление коэффициентами находится в правом верхнем углу экрана. Параметр efficiency коэффициент эффективности управления, параметр damping коэффициент демпфирования, взятый с обратным знаком.
Управление игрой:
- Пробел старт игры;
- W/S вращение вокруг оси Z ССК, нос вниз/нос вверх;
- A/D вращение вокруг оси Y ССК, поворот влево/поворот вправо;
- 4/6 на нумпаде вращение вокруг оси X ССК, крен левый/крен правый.
На индикаторе лобового стекла игрок видит искусственный горизонт, а также текущие значения курса (heading) и глубины (depth), то есть расстояния до опасной поверхности. Также показывается остаток времени игры и текущий результат (score) количество посещенных локаций.
Код симулятора написан на JavaScript с применением библиотеки Three.js. Значения параметров движения объекта обновляются в игровом цикле численным интегрированием уравнения (1) по методу Эйлера. В каждой итерации вызывается метод update() объекта vehicle, выполняющий вычисления для каждого канала управления:
vehicle.update = function () { //определение интервала времени в секундах: game.elapsed = (new Date() - game.time) / 1000; game.time = new Date(); //другие действия... //обновление значений угловой скорости в радианах в секунду: vehicle.omegaX += (vehicle.epsilonX - vehicle.omegaX * vehicle.damping) * game.elapsed; vehicle.omegaY += (vehicle.epsilonY - vehicle.omegaY * vehicle.damping) * game.elapsed; vehicle.omegaZ += (vehicle.epsilonZ - vehicle.omegaZ * vehicle.damping) * game.elapsed; //другие действия...}
Поля epsilonX, epsilonY и epsilonZ объекта vehicle содержат составляющие углового ускорения при отсутствии демпфирования. Значение каждого из этих полей получается умножением входного сигнала на коэффициент эффективности управления:
function init() { //другие действия... //ввод с клавиатуры: document.addEventListener('keydown', function (event) { if (game.state == "READINESS") if (event.code == "Space") { //запуск игры... } if (game.state == "RUN") switch (event.code) { case "KeyW": vehicle.epsilonZ = vehicle.efficiency; break; case "KeyS": vehicle.epsilonZ = -vehicle.efficiency; break; case "KeyA": vehicle.epsilonY = -vehicle.efficiency; break; case "KeyD": vehicle.epsilonY = vehicle.efficiency; break; case "Numpad4": vehicle.epsilonX = vehicle.efficiency; break; case "Numpad6": vehicle.epsilonX = -vehicle.efficiency; break; } }); document.addEventListener('keyup', function (event) { switch (event.code) { case "KeyW": vehicle.epsilonZ = 0; break; case "KeyS": vehicle.epsilonZ = 0; break; case "KeyA": vehicle.epsilonY = 0; break; case "KeyD": vehicle.epsilonY = 0; break; case "Numpad4": vehicle.epsilonX = 0; break; case "Numpad6": vehicle.epsilonX = 0; break; } }); //другие действия...}
Результаты эксперимента
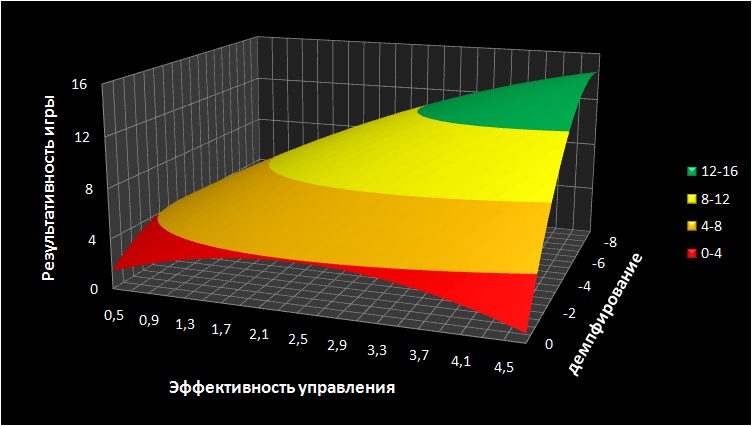
Показатель качества модели будем рассматривать как функцию двух переменных. Соответственно, результаты исследования в графическом виде представляют собой 3D-поверхность, каждая точка которой определяет свою модель управляемого объекта.

Рассмотрим ключевые особенности некоторых моделей. На графике обсуждаемые модели обозначены латинскими буквами.
При минимальном значении коэффициента эффективности управления (0,5 рад/с2) существует модель с наилучшим значением коэффициента демпфирования (точка А). Модель А характеризуется слабой способностью объекта к динамичным маневрам.
Изменение модели А в сторону усиления демпфирования приводит к созданию моделей, имеющих крайне низкие максимальные значения угловой скорости. Объект окончательно теряет способность к маневрированию.
Изменение модели А в сторону снижения демпфирования частично улучшает маневренность объекта, но общее качество системы падает за счет ухудшения ее динамических свойств: возникает проблема раскачки, управление требует от игрока постоянных компенсирующих действий.
При отсутствии демпфирования существует модель с оптимальной эффективностью управления (В). Ее эффективность управления выше, чем у модели А, что обеспечивает хорошую маневренность. При этом проблема раскачки усугубляется по сравнению с моделью А, полностью лишенной демпфирования.
Изменение модели B в сторону повышения эффективности управления доводит проблему раскачки до уровня, когда борьбе с ней уделено все внимание игрока. Далее маневрирование без выхода за ограничения становится невозможным.
Модель C объединяет достоинства моделей A и B. Объект управляется достаточно эффективно, но без раскачки. Значение показателя результативности игры у модели C заметно выше, чем у предыдущих моделей. Тем не менее, эта модель не является наиболее результативной.
Форма изолиний результативности игры в окрестностях точки C показывает, что улучшению результата соответствует движение в направлении модели D.
Это движение соответствует снижению значения T при сохранении k на постоянном уровне (около 0,6 рад/с). Модели, расположенные между C и D, превосходят C по результативности игры. В игре с этими моделями объект управления более четко следует нажатиям клавиш.
При движении от модели C к модели D происходит еще одно изменение: ухудшение естественности поведения объекта. Постоянная времени приближается к уровню, при котором длительность переходного процесса и сдвиг фазы выходного сигнала перестают быть заметными для пользователя.
Изменение модели D в сторону дальнейшего снижения значения T при сохранении значения k уже не дает существенных улучшений, потому что сдвиг фазы выходного сигнала и длительность переходного процесса у модели D и без того достаточно малы для восприятия игрока.
Модели, получаемые дальнейшим улучшением D, с точки зрения игрока ничем не отличаются от реализации усилительного звена: в игре отсутствует угловое ускорение объекта, угловая скорость при нажатии клавиши мгновенно принимает установившееся значение.
Проведенный анализ позволяет сделать следующие выводы:
1. Оптимальные значения параметров модели соответствуют ее вырождению в усилительное звено (значение k составляет около 0,6 рад/с, T = 0 с) и потере естественности поведения объекта.
2. Модель, обеспечивающая хорошую управляемость при естественном поведении объекта, соответствует точке C на графике (коэффициент эффективности управления: от 2 до 3 рад/с2; коэффициент демпфирования: от -4,5 до -3,5 1/с).
3. Изменение модели C в направлении снижения значения T при k = const позволяет получить объект с улучшенной управляемостью за счет ухудшения естественности его поведения.
Неучтенные факторы
Вместе с упрощениями физики управляемого объекта на качество результатов исследования влияют и другие упрощения условий исследования:
1. Модель управляемости описывалась двумя значениями параметров, во всех каналах управления объект вел себя одинаково. Для получения точной картины следует варьировать значения шести параметров, поскольку нет оснований считать свойства игрока одинаковыми для всех каналов.
2. Полученные результаты актуальны для настроек поля зрения камеры, используемых в игре. Изменение этого параметра окажет заметное влияние на взаимодействие игрока с объектом.
Наиболее серьезный недостаток исследования отсутствие статистики. Любое эргономическое исследование должно ориентироваться на свойства целевой аудитории в целом. Более полные результаты могут быть получены при участии группы игроков.













































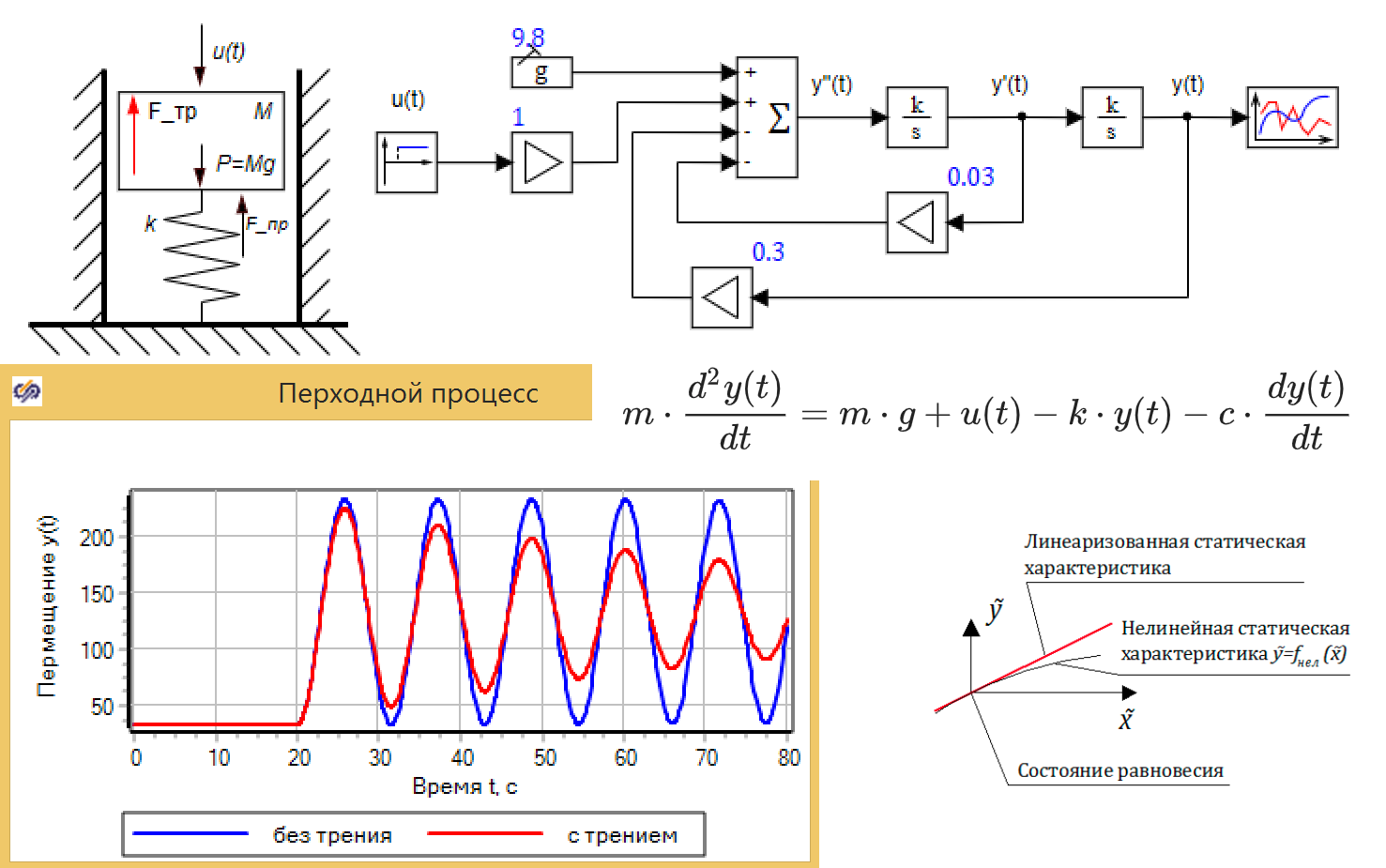





























 Рисунок 3.3.1 Расчетная схема камеры смешения
Рисунок 3.3.1 Расчетная схема камеры смешения
 Рисунок 3.3.2 Годограф АФЧХ
апериодического звена 1-го порядка
Рисунок 3.3.2 Годограф АФЧХ
апериодического звена 1-го порядка
 Рисунок 3.3.3 АЧХ апериодического звена 1-го
порядка
Рисунок 3.3.3 АЧХ апериодического звена 1-го
порядка Рисунок 3.3.4 ФЧХ апериодического звена 1-го порядка
Рисунок 3.3.4 ФЧХ апериодического звена 1-го порядка
 Рисунок 3.3.5 ЛАХ и ЛФЧХ апериодического
звена 1-го порядка
Рисунок 3.3.5 ЛАХ и ЛФЧХ апериодического
звена 1-го порядка
 Рис.3.3.6 Переходная функция
апериодического звена 1-го порядка
Рис.3.3.6 Переходная функция
апериодического звена 1-го порядка Рис.3.3.7 Весовая функция апериодического
звена 1-го порядка
Рис.3.3.7 Весовая функция апериодического
звена 1-го порядка
 Рисунок 3.3.8 Примеры апериодических
звеньев 1-го порядка
Рисунок 3.3.8 Примеры апериодических
звеньев 1-го порядка
 Рисунок 3.3.9 Частотный анализ модели
камеры смешения в виде стандартного апериодического звена
Рисунок 3.3.9 Частотный анализ модели
камеры смешения в виде стандартного апериодического звена
 Рисунок 3.3.10 Годограф модели камеры
смешения в виде Инерционного звена первого порядка.
Рисунок 3.3.10 Годограф модели камеры
смешения в виде Инерционного звена первого порядка.
 Рисунок 3.3.11 Модель камеры смешения в коде НS.
Рисунок 3.3.11 Модель камеры смешения в коде НS.
 Рисунок 3.3.12 Температура в узле в
начальный период расчета.
Рисунок 3.3.12 Температура в узле в
начальный период расчета.
 Рисунок 3.3.13 Настройка файлов рестартов.
Рисунок 3.3.13 Настройка файлов рестартов.
 Рисунок 3.3.13 Пакет для сравнения
моделей узла смешения.
Рисунок 3.3.13 Пакет для сравнения
моделей узла смешения.
 Рисунок 3.3.14 Сравнение переходного
процесса для разных моделей камеры смешения.
Рисунок 3.3.14 Сравнение переходного
процесса для разных моделей камеры смешения.
 Рисунок 3.3.15 Колебания давления и
расхода при ступенчатом изменении температуры.
Рисунок 3.3.15 Колебания давления и
расхода при ступенчатом изменении температуры.
 Рисунок 3.3.16 Модель частотного анализа
внешней системы.
Рисунок 3.3.16 Модель частотного анализа
внешней системы.
 Рисунок 3.3.17 Скрипт гидравлической модели.
Рисунок 3.3.17 Скрипт гидравлической модели.
 Рисунок 3.3.18. Результаты анализа
частотного анализа гидравлической модели.
Рисунок 3.3.18. Результаты анализа
частотного анализа гидравлической модели.
 Рисунок 3.3.19 Давление в узле и расход в
выходном канале с ростом частоты воздействия по температуре.
Рисунок 3.3.19 Давление в узле и расход в
выходном канале с ростом частоты воздействия по температуре.
 Рисунок 3.5.1 Модель электического
колебательного контура
Рисунок 3.5.1 Модель электического
колебательного контура
 Рисунок 3.5.2 АЧХ колебательного звена
Рисунок 3.5.2 АЧХ колебательного звена Рисунок 3.5.3 ФЧХ колебательного звена
Рисунок 3.5.3 ФЧХ колебательного звена
 Рисунок 3.5.4 АФЧХ колебательного звена
Рисунок 3.5.4 АФЧХ колебательного звена Рисунок 3.5.5 Годограф АФЧХ консервативного звена
Рисунок 3.5.5 Годограф АФЧХ консервативного звена
 Рисунок 3.5.6 ЛАХ колебательного звена
Рисунок 3.5.6 ЛАХ колебательного звена
 Рисунок 3.5.6 Переходная функция консервативного
звена
Рисунок 3.5.6 Переходная функция консервативного
звена
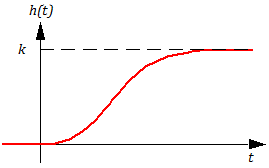 Рисунок 3.5.8 Переходная функция
колебательного звена (при = 1)
Рисунок 3.5.8 Переходная функция
колебательного звена (при = 1) Рисунок 3.5.9 Переходная функция
колебательного звена (при 0 < < 1)
Рисунок 3.5.9 Переходная функция
колебательного звена (при 0 < < 1)
 Рисунок 3.5.10 Весовая функция
колебательного звена при = 0.
Рисунок 3.5.10 Весовая функция
колебательного звена при = 0.
 Рисунок 3.5.11 Весовая функция
колебательного звена при = 1.
Рисунок 3.5.11 Весовая функция
колебательного звена при = 1.
 Рисунок 3.5.12 Весовая функция
колебательного звена при 0 < < 1.
Рисунок 3.5.12 Весовая функция
колебательного звена при 0 < < 1.
 Рисунок 3.5.13 Модель колебательного контура
Рисунок 3.5.13 Модель колебательного контура
 Рисунок 3.5.14 Общие сигналы проекта.
Рисунок 3.5.14 Общие сигналы проекта. Рисунок 3.5.15. Вычисление параметров для
колебательного звена.
Рисунок 3.5.15. Вычисление параметров для
колебательного звена.
 Рисунок 3.5.16. Графики напряжений
источника и на конденсаторе.
Рисунок 3.5.16. Графики напряжений
источника и на конденсаторе.
 Рисунок 3.5.17 Сравнение модели контура и
колебательного звена
Рисунок 3.5.17 Сравнение модели контура и
колебательного звена
 Рисунок 3.5.18. Частотный анализ
электрического контура
Рисунок 3.5.18. Частотный анализ
электрического контура
 Рисунок 3.5.19 Результаты гармонического анализа.
Рисунок 3.5.19 Результаты гармонического анализа.
 Рисунок 3.5.20 Модель с изменяемыми
параметрами контура.
Рисунок 3.5.20 Модель с изменяемыми
параметрами контура.
 Рисунок 3.5.21. Скрипт изменения параметров модели
Рисунок 3.5.21. Скрипт изменения параметров модели
 Рисунок 3.5.22. Настройки контура для
устранения колебаний
Рисунок 3.5.22. Настройки контура для
устранения колебаний Рисунок 3.5.23. Графики изменения
переходных процессов в контуре при изменении R и С.
Рисунок 3.5.23. Графики изменения
переходных процессов в контуре при изменении R и С.
 Рисунок 3.5.24 Схема колебательного
контура с настройками частоты источника.
Рисунок 3.5.24 Схема колебательного
контура с настройками частоты источника.
 Рисунок 3.5.24 Скрипт для управления и
отображения частоты.
Рисунок 3.5.24 Скрипт для управления и
отображения частоты.

 Рисунок 3.7.1 Эквивалентная структурная
схема форсирующего звена
Рисунок 3.7.1 Эквивалентная структурная
схема форсирующего звена
 Рисунок 3.7.2 АФЧХ форсирующего звена
Рисунок 3.7.2 АФЧХ форсирующего звена Рисунок 3.7.3 АЧХ и ФЧХ форсирующего звена
Рисунок 3.7.3 АЧХ и ФЧХ форсирующего звена
 Рисунок 3.7.4 ЛАХ и ЛФЧХ форсирующего звена
Рисунок 3.7.4 ЛАХ и ЛФЧХ форсирующего звена
 Рисунок 3.7.5 Переходная функция форсирующего
звена
Рисунок 3.7.5 Переходная функция форсирующего
звена Рисунок 3.7.6 Весовая функция форсирующего звена
Рисунок 3.7.6 Весовая функция форсирующего звена
 Рисунок 3.7.7 Модель камеры смешения с
узлом регулирования температуры
Рисунок 3.7.7 Модель камеры смешения с
узлом регулирования температуры
 Рисунок 3.7.8 Модель системы управления
Рисунок 3.7.8 Модель системы управления
 Рисунок 3.7.9 Выбор типа регулятора в настройках
Рисунок 3.7.9 Выбор типа регулятора в настройках
 Рисунок 3.7.10. Скрипт изменения заданной
температуры
Рисунок 3.7.10. Скрипт изменения заданной
температуры
 3.7.11 Проект и скрипт для сравнения двух рассчетов
3.7.11 Проект и скрипт для сравнения двух рассчетов
 Рисунок 3.7.12 Сравнение П и ПД регуляторов
Рисунок 3.7.12 Сравнение П и ПД регуляторов