Мы живем буквально в преддверии эпохи квантовых компьютеров. Первые экспериментальные машины уже прямо сейчас доступны для тестирования благодаря облачным технологиям и об этом мы отдельно поговорим в конце статьи.
Но имя одного из крупнейших физиков XX века, плоды работы которого мы пожинаем сейчас, спустя 100 лет, часто остается за кадром. Шатьендранат Бозе мало кому известен за пределами родной страны. Западные СМИ вспоминают его исключительно в паре с Эйнштейном, ограничиваясь только фамилией.
Перед вами биография ученого из Индии, патриота и мыслителя. Он сделал для своей страны не меньше, чем его современница Ся Пейсу для Китая.
Страну создают не только её культура и традиции. Крупнейшие государства покоятся на плечах ученых, которые, подобно атлантам, закладывают фундамент для будущего процветания своих сограждан.

Человек, которому подчиняется половина частиц во Вселенной именно так однажды профессор физики представил Шатьендраната Бозе своим студентам. Бозе был ученым-энтузиастом. Эрудитом, заложившим основы статистики Бозе Эйнштейна и теории конденсата Бозе Эйнштейна.
Несколько крупных ученых получили Нобелевскую премию за исследования, связанные с областью науки, которую фактически открыл Бозе. Однако его самого премия обошла. Есть ли повод для грусти? Вряд ли. Титул повелителя половины частиц во вселенной сам по себе значит немало.
Ранние годы жизни
Шатьендранат Бозе родился 1 января 1894 года в Калькутте. Он был старшим сыном в большой и сравнительно небедной семье, у него было семь младших сестер. С малых лет Бозе проявлял недюжинные способности к учебе и жаждал знаний.
Его отец, Шурендранат, работал бухгалтером и всеми силами поощрял способности сына. Каждое утро, уходя на работу, он записывал на полу веранды домашнее задание для сына арифметические задачи. Бозе решал их и вечером с гордостью показывал готовые примеры отцу.
В возрасте 13 лет мальчика отдали в известную школу в Центральной Калькутте. Там способности Шатьендраната также не остались без внимания. Учителя признавали, что в области математики и естественных наук ему не было равных и это в престижной школе, где и преподаватели, и ученики были как на подбор.
В 1909 году, когда ему шел шестнадцатый год, Бозе принял решение пройти промежуточный курс естественных наук в Президентском университете.
А тем временем на Западе Альберт Эйнштейн уже был заслуженно известен своей специальной теорией относительности, опубликованной в 1905 году.
Преподавателями Шатьендраната в Президентском колледже были знаменитые Джагадиш Чандра Бос и сэр Прафулла Чандра Рэй. В 17 лет он успешно сдал промежуточные экзамены и спустя два года стал бакалавром наук в области математики. Стоит ли говорить, что Шатьендранат снова был лучшим в своем классе.

В 1915 году в возрасте 21 года Бозе стал магистром прикладной математики Калькуттского университета. При этом ему удалось установить абсолютный рекорд среднего балла 92%.
На Западе началась Первая мировая Война. Альберт Эйнштейн публикует общую теорию относительности.
Логичным продолжением карьеры любого ученого является получение докторской степени. Любого, но не Бозе. Это было бы слишком просто. Докторской диссертации он предпочел преподавание. С 1916 по 1921 год он читал лекции студентам физического факультета университета Калькутты.
Приблизительно в это время в руки Бозе попала только-только опубликованная общая теория относительности. Труд Эйнштейна очаровал Бозе настолько, что, заручившись помощью своего друга, он в кратчайшие сроки перевел научные работы Эйнштейна с немецкого языка на английский и опубликовал их сборник.
Отдельно отметим, что Бозе был полиглотом. Он хорошо знал множество языков. Среди них бенгали, английский, французский, немецкий и санскрит.
В том же 1921 году Эйнштейн был удостоен Нобелевской премии за заслуги в области теоретической физики. В частности за объяснение фотоэффекта. Это был поворотный шаг в развитии квантовой теории. И вряд ли во всей Индии нашелся бы более преданный фанат Эйнштейна, чем Бозе.
Прорыв
В том же году Бозе покинул родную Калькутту и устроился лектором на физическом факультете Университета Дакки (Бангладеш). Вот что он говорил о ситуации в университете в письме своему другу:
Прошло уже больше месяца со дня моего переезда в твою часть страны. Работа все еще не началась. В университете было ценных вещей, однако из-за тотальной халатности они пришли в удручающее состояние. Кроме того, мы страдаем от нехватки научной прессы. Руководство пообещало оформить несколько подписок и приобрести старые номера. Поговаривают даже об отдельной научной библиотеке
Благодаря стараниям Бозе в университете открылись новые кафедры и лаборатории в частности, продвинутые курсов для студентов факультетов физики и химии. Своим студентам Бозе читал лекции по термодинамике и классическому электромагнетизму.

Как раз во время одной из своих лекций Бозе почувствовал, что существующие выводы из закона излучения Планка неполны. После долгих раздумий и консультаций с коллегами Бозе опубликовал статью, в которой без использования классической физики он приходит к тем же результатам, что и сам Планк. Это был настоящий прорыв. Поначалу выведенная им формула была отвергнута учеными как радикальная и противоречащая консервативным научным взглядам. Но он не унывал. Вместо этого он отправил свою статью непосредственно Альберту Эйнштейну в Германию.

В каком-то смысле Бозе помог Эйнштейну возродить свою научную карьеру. Иронично пионер квантовой революции в начале 1920-х активно препятствовал ей. Письмо Бозе оказалось отрезвляющим глотком свежего воздуха и заняло внимание великого ученого.
Эйнштейн сразу же осознал, какое значение имеет письмо от молодого индийского физика. Его стараниями статья Бозе была переведена на немецкий и опубликована в Zeitschrift fr Physik, популярном немецком научном издании. Так родилась статистика Бозе Эйнштейна.
Эйнштейн был крайне впечатлен тем, что ради научного прогресса никому не известный молодой ученый из Индии решился отправить ему свою спорную статью. Позднее он писал Бозе: Ваша статья важный шаг вперед. И она мне очень нравится!.
Чем больше Эйнштейн размышлял о статье, тем сильнее она влияла на его мировоззрение. Причина, по которой работа Бозе дала точные результаты, крылась в том, что, поскольку фотоны неотличимы друг от друга, нельзя рассматривать любые два фотона с одинаковой энергией как два разных фотона. Это довольно простая для понимания мысль. Рассмотрим пример.
Вы одновременно подбрасываете две различимые и несмещенные монеты в воздух. Существует 4 возможных результата:

Вероятность того, что выпадет два орла составляет всего 1/4. Но все меняется, если сделать монеты неотличимыми друг от друга. В этой ситуации возможны уже три исхода: одновременно два орла, одновременно две решки и орел + решка. Таким образом, шанс выпадения двух орлов увеличивается до 1/3. В мире статистики Бозе вероятность возникновения тех или иных событий может отличаться от наших ожиданий.
Эйнштейн осознал важность этого предположения даже раньше, чем сам Бозе. Он воспринял идею индийского ученого и распространил её на атомы. Это позволило Эйнштейну предсказать существование феномена, известного нам как конденсат Бозе Эйнштейна.
Конденсат Бозе Эйнштейна это так называемое пятое состояние материи. В нем каждый атом становится неотличим от других, и образуется гигантский суператом. В обычном газе атомы находятся в беспорядочном движении с очень высокой скоростью, в то время как в случае с конденсатом Бозе Эйнштейна они остаются вместе в состоянии совершенной гармонии.
Только в 1995 году, спустя 70 лет после того, как было сделано это предсказание, ученым удалось обнаружить существование конденсата Бозе Эйнштейна.
Эта работа стала для Бозе ключом к сотрудничеству с самыми видными учеными Европы тех лет. Для этого он подал заявление на двухлетний отпуск. Университет отпустил Бозе только после того, как он показал вице-канцлеру университета благодарственное письмо от Эйнштейна.

По прибытии в Париж Бозе написал своему кумиру:
Университет предоставил мне двухгодичный отпуск. Всего неделю назад я впервые приехал в Париж. Не знаю, получится ли у меня продолжить свою работу под вашим руководством в Германии. Однако, если вы согласитесь стать моим руководителем, исполнится моя давняя мечта.
С нетерпением Бозе ждал, что Эйнштейн ответит на его просьбу. В то же самое время ему посчастливилось познакомиться с Марией Кюри и помочь ей провести некоторые измерения пьезоэлектрического эффекта. Затем Морис де Бройль лично ознакомил Бозе с дифракцией рентгеновских лучей и спектроскопией. Наконец, пришел ответ от Эйнштейна:
Искренне благодарен вам за письмо. Рад, что скоро у меня будет возможность познакомиться с вами лично.
Бозе отправился в Берлин. Поработать с самим Эйнштейном у него не вышло, однако встреча с мэтром принесла свои плоды. Эйнштейн написал для Бозе рекомендательное письмо. Это позволило ему познакомиться с лучшими немецкими учеными: Фрицем Габером, Лизой Мейтнер и Максом Борном.

В 1926 году Бозе вернулся в Дакку. Ему было 32 года, но без докторской степени он не мог претендовать на должность профессора. Ситуацию спасло все то же письмо Эйнштейна: Бозе был назначен главой факультета физики университета Дакки.
Знания, полученные в Европе, помогли Бозе реформировать университет. Он самостоятельно разработал оборудование для лаборатории рентгеновской кристаллографии. Построил массу других лабораторий, выбил у руководства бюджет на строительство библиотеки. Под его руководством также был открыт центр исследований в области унифицированных теорий поля. Вплоть до 1945 года Бозе продолжал активную работу на факультете.

Когда раздел Индии стал неизбежен, ему пришлось вернуться в Калькутту. Отделение Пакистана виделось ему огромной раной в сердце любимой страны. Из-за депрессии у Бозе не получалось сосредоточиться на научных изысканиях.
Он преподавал в родном городе до самой пенсии. Новаторские идеи принесли Бозе восхищенные отзывы Эйнштейна и коллег по цеху. Обеспечили место в пантеоне крупнейших ученых-физиков. Но мало кто знает о человеческих качествах Бозе. Он был не просто ученым, но человеком, который хотел постичь окружающий мир во всей его полноте, во всей сложности. И непосредственно научная работа была лишь малой частью его собственной вселенной.

Кроме того, он был страстным патриотом. Много сил он потратил на продвижение бенгальского как языка, на котором ведется преподавание. Бозе лично перевел десятки статей на бенгальский. Он считал своим долгом открыть науку своим соотечественникам на их родном языке.
Пенсия
В 62 года Бозе оставил работу и вышел на пенсию, получив статус почетного профессора. Последовали бесчисленные приглашения на крупные мероприятия и вечеринки. Бозе отвергал большую часть приглашений. Не хватало ставшего привычным удовольствия от науки. Постоянного поиска новых знаний и свершения открытий. Поэтому спустя короткое время он вернулся в Калькуттский университет и продолжил исследования в области ядерной физики, органической химии и единой теории поля. Здесь он был на своем месте.
Как раз в это время Поль Дирак, знаменитый физик, посетил Калькутту вместе со своей женой. Примечательна история одной из совместных поездок Бозе и Дирака.
Комфортное заднее сиденье в машине получили Дирак и его супруга. Крупный Бозе сел впереди, рядом с водителем. В попутчики Бозе взял двух своих учеников. Каким-то образом всем удалось разместиться рядом с Бозе на переднем сиденье. На удивленный вопрос о том, не тесновато ли им, Бозе рассмеялся и обезоруживающим тоном ответил: Мы верим в статистику Бозе-Эйнштейна. А, как пояснил Дирак удивленной жене, в статистике Бозе-Эйнштейна всё очень тесно связано.
Именно Дирак, ставший близким другом Бозе, предложил термин бозон в память о вкладе ученого в теоретическую физику.
В 1958 году Бозе избрали членом Лондонского Королевского Общества. Год спустя правительство назначило его национальным профессором. Бозе занимал эту должность вплоть до своей кончины. Как уже было сказано выше, Нобелевскую премию он так и не получил. Когда Бозе спросили, что он думает по этому поводу, он скромно ответил: Я получил всё признание, которого заслуживаю.
Он умер в Калькутте в возрасте 80 лет. С ним ушла целая эпоха. Без натяжки можно сказать, что Шатьендранат Бозе один из величайших физиков Индии. И не только на основании его научных достижений, но и потому что он искренне любил свою страну.
Новость вместо заключения
В самом начале статьи мы обещали, что еще вернемся к теме квантовых вычислительных систем. Современные технологии делают доступным то, что когда-то можно было увидеть только в крупных научных лабораториях. Уже не первый год существуют квантовые вычислительные системы, доступ к которым обеспечивается облачными решениями.
В начале сентября стало известно о еще одном перспективном проекте. Исполнит ли он собственные обещания или окажется очередным журналистским квантовым утенком, покажет время. Приведем здесь короткое описание канадского проекта Xanadu.
2 сентября компания Xanadu (Занаду) из Торонто объявила о запуске первой в мире общедоступной платформы фотонных квантовых вычислений. Клиенты платформы смогут получить доступ к 8-, 12- и (в ближайшем будущем) к 24-кубитным машинам через облако.
По словам Кристиана Уидбрука, основателя и генерального директора Xanadu, каждые шесть месяцев компания собирается удваивать количество кубитов в своих облачных системах. В ближайшие месяцы Xanadu планирует опубликовать документ о фотонных квантовых вычислений, который, по сути, будет представлять из себя учебник о том, как масштабироваться до миллионов кубитов.
Принцип работы Xanadu, квантовые вычисления с непрерывными переменными, не использует генераторы одиночных фотонов. Вместо них применяются так называемые сжатые состояния, состоящие из суперпозиций множества фотонов.













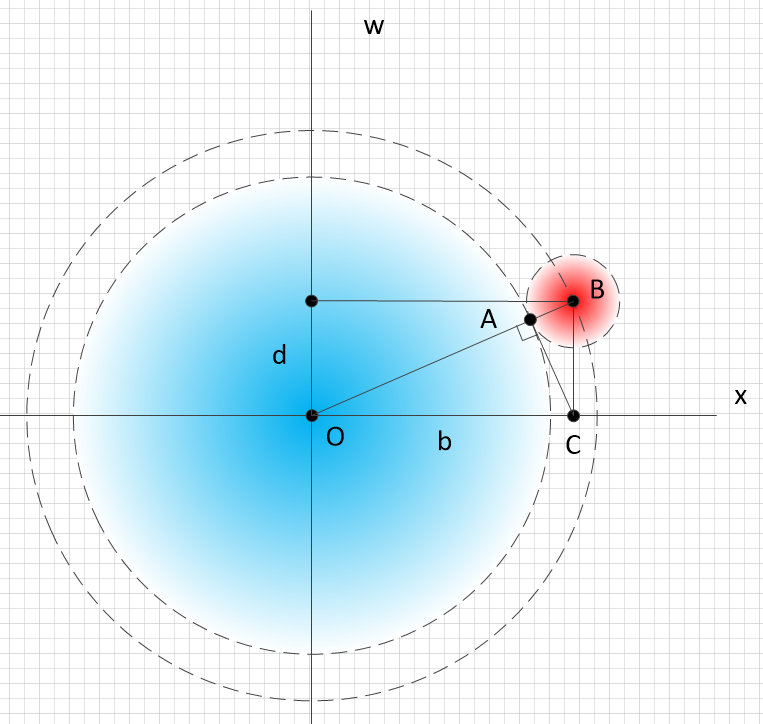













 Рисунок из статьи Рёмера. Рёмер наблюдал
затмения в точках E. K. L. H, G, F
Рисунок из статьи Рёмера. Рёмер наблюдал
затмения в точках E. K. L. H, G, F
 Схема
измерения скорости света
Схема
измерения скорости света
 Синхронизация Эйнштейна. Время t вторых
часов определяется таким образом, чтобы оно равнялось половине
времени, за которое свет проходит расстояние 2*AB
Синхронизация Эйнштейна. Время t вторых
часов определяется таким образом, чтобы оно равнялось половине
времени, за которое свет проходит расстояние 2*AB
 Пространственно-временная диаграмма. Для
наблюдателей два случая идентичны, но часы синхронизированы
по-разному
Пространственно-временная диаграмма. Для
наблюдателей два случая идентичны, но часы синхронизированы
по-разному
 Текст статьи можно найти на сайте журнала
Текст статьи можно найти на сайте журнала









