Математика на пальцах

Математика верстальщику не нужна!, говорили они. Арифметики за 2 класс школы хватит!, говорили они. Верстальщик не программист, так что нечего себе голову забивать точными науками!, чего только не услышишь на просторах интернета на тему нужности тех или иных знаний при разработке сайтов. И на самом деле в большинстве случаев человеку, который делает интерфейсы, и правда хватает умения складывать числа. Что-то более сложное встречается редко и обычно уже есть готовый алгоритм где-то в недрах NPM. Но сайты понятие растяжимое, и иногда все же нужно включить голову, и разобраться в каком-то вопросе. И один из таких вопросов это траектории в 2D анимациях.

Наблюдая за людьми, которые осваивают JS, и, в частности, покадровые анимации в вебе, я заметил, что у многих возникают сложности, когда нужно сделать движение какого-то объекта на странице по определенной траектории. И, если эта траектория не нарисована заранее заботливым дизайнером в виде path в SVG-картинке, а формулируется какими-то общими словами и ссылками на референсы из сети, или, что еще хуже, должна генерироваться на лету, то задача приводит их в полный ступор. По всей видимости все упирается в тотальное непонимание того, как получить кривую той или иной формы в рамках JS. Об этом мы сегодня и поговорим в формате своеобразной лекции о временных функциях для анимаций в самых разных их проявлениях.

Мы постараемся избежать излишней теоретизации, отдавая предпочтение картинкам и объяснению всего на пальцах, с акцентом на практическое использование в вопросах 2D анимаций на сайтах. Так что местами формулировки могут быть не совсем точными с точки зрения математики или не совсем полными, цель этой статьи дать общее представление о том, что бывает, и откуда можно начать в случае чего.

Немного определений

Школьная программа имеет свойство выветриваться из готовы после покидания этой самой школы, но все же такое понятие, как декартова система координат должно остаться. В работе с HTML и CSS мы постоянно к ней обращаемся. Две перпендикулярных оси, которые обычно обозначаются буквами X и Y, одинаковый масштаб по обеим осям это именно она. Декартова система координат это частный случай прямоугольной системы координат, у которой масштаб по осям может быть разным. Такие системы координат в вебе тоже встречаются, правда чаще в вопросах, связанных с канвасом и WebGL. Вопросы переходов между системами координат в общем случае мы пока отложим, так как это не будет нужно для решения текущих задач. Сейчас нам важно научиться делать кривые определенной формы.

Второе понятие, которое нам пригодится это график функции. В нашем случае функция это зависимость чего-то одного от чего-то другого. Дали что-то на вход получили что-то на выходе. Давая функции на вход разные значения получаем разные значения на выходе. А может и не разные. А может она вообще определена только для определенного набора значений. Всякое может быть. В любом случае такие наборы значений можно отобразить в виде графиков в той или иной системе координат на наш вкус.

Вы конечно спросите, каким образом связаны графики и анимации? Представьте себе канвас. Вы рисуете на нем точку. И начинаете ее двигать, в каждом кадре очищая канвас и рисуя ее в новом месте. Или еще лучше, если это будет кружочек, имитирующий мячик. Он будет подпрыгивать, отскакивая от пола. Представьте это. А теперь представьте, что получится, если между кадрами не очищать канвас? Там будет оставаться след от мячика, причем он будет не совсем случайным, а в виде кривой линии, напоминующей много парабол, соединенных между собой. Так вот, нам нужно решить обратную задачу сначала сделать эту кривую линию, график некоторой функции, а потом уже вдоль нее двигать мячик, постепенно меняя параметры функции и получая каждый раз новое положение для него. А этим мячиком уже может быть что угодно HTML-элемент, что-то в SVG-картинке, что-то на канвасе не важно.

I. Простые функции вида y = f(x) и коэффициенты

Начнем мы с простых функций. Из школьной тригонометрии вы должны помнить такие слова, как синус, косинус, тангенс, котангенс, и.т.д. В примерах будет часто использоваться синус, но все идеи и приемы будут универсальными их можно использовать с чем угодно и как угодно.

Давайте посмотрим на график синуса:

(x) => {    return Math.sin(x);}

Примеры функций-зависимостей в виде кода будут на условном JS.

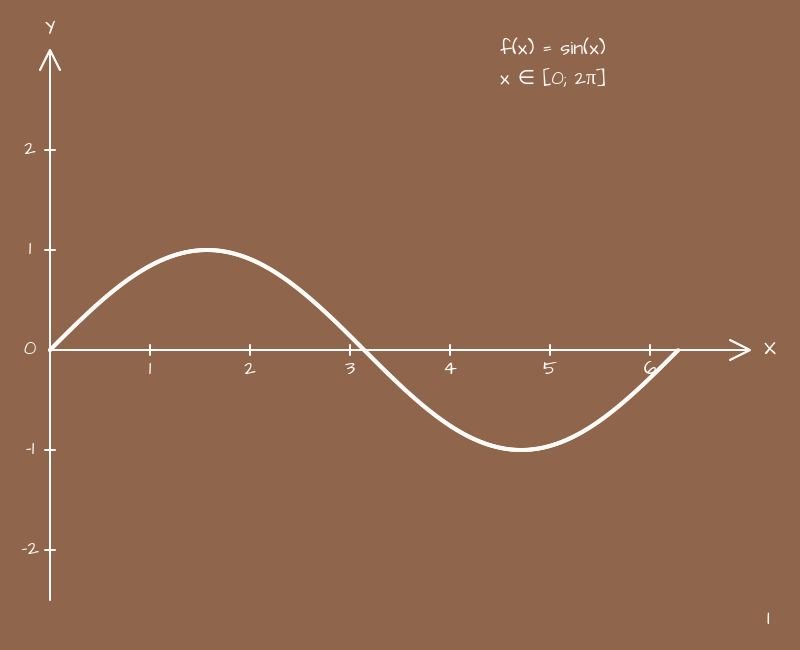
Здесь у нас две оси, X и Y, и Y зависит от X. Если мы будем менять X от 0 до 10 (условно), то Y будет плавать туда-сюда, туда-сюда, туда-сюда Если нужно сделать покачивание чего-то на странице это то, что нужно. Мы можем использовать requestAnimationFrame и в каждом кадре слегка увеличивать x, использовать нашу пока еще простую функцию для вычисления y, и таким образом каждый раз получать новые координаты для какого-то объекта. И, разумеется, никто не мешает оставить объект на одном месте по оси X, а менять только его положение по Y здесь уже все зависит от задачи.

Но тут есть нюанс обычно мы мыслим в пикселях, десятках и сотнях пикселей, а здесь координаты будут слишком маленькими. Нужно будет весь этот график подвинуть куда-то по экрану, или растянуть, или еще что-то с ним сделать. Будет очень полезно разобраться с тем, как те или иные коэффициенты влияют на конечный результат, чтобы потом добавлять их на уровне интуиции.

Первым делом будут множители:

(x) => {    return 2 * Math.sin(x);}(x) => {    return 0.5 * Math.sin(5 * x);}

Они будут растягивать или сжимать наш график.

Умножая параметр (x в наших примерах) на какой-то коэффициент, мы получаем растяжение или сжатие по оси X. Умножая всю функцию на коэффициент получаем растяжение или сжатие по оси Y. Здесь все просто.

Добавим еще коэффициентов, только на этот раз не в виде множителей, а в виде слагаемых:

(x) => {    return Math.sin(x) + 1;}(x) => {    return Math.sin(x + 1);}

Что же там получилось?

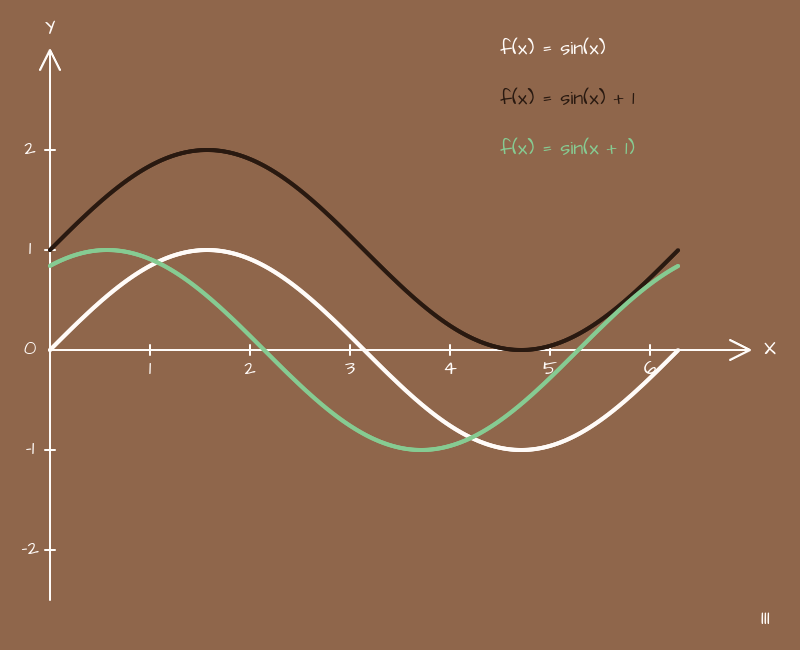
Очевидно график смещается. Добавляем коэффициент к параметру x получаем смещение по X, добавляем коэффициент ко всей функции получаем смещение по Y. Тоже, ничего сложного.

Эти же соображения действуют для всех подобных функций, не только для синуса.

Здесь у нас останется еще вопрос поворота всего графика. Для этого нам понадобится матрица поворота, но тема матриц и преобразований координат достойна отдельной статьи, так что сейчас мы лишь упомянем это ключевое слово и пойдем дальше.

Что будет, если сложить две синусоиды с разными коэффициентами? Давайте посмотрим!

(x) => {    return Math.sin(x) + 0.2 * Math.sin(5 * x);}

Получается что-то такое:

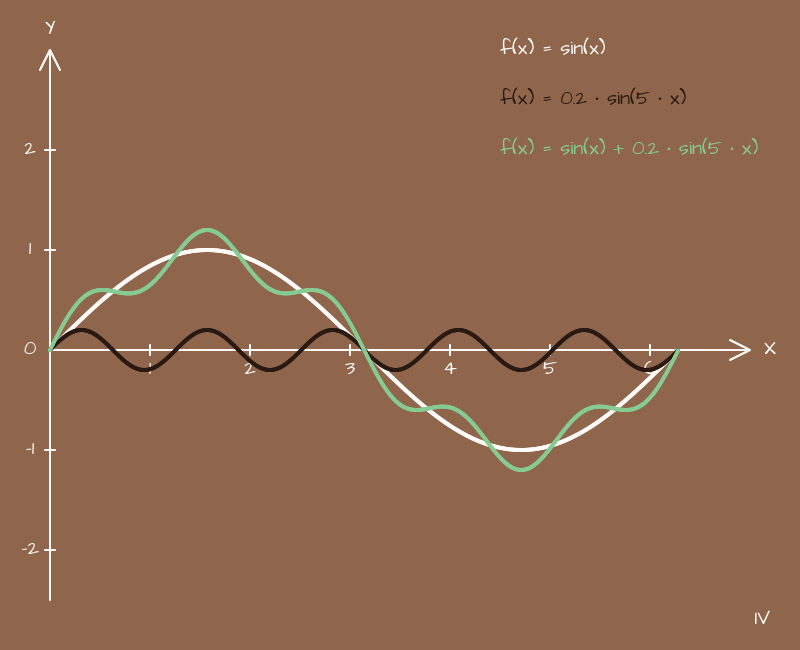
Если вы когда-то работали со звуковыми файлами или даже осциллографом в виде отдельного прибора, то наверное уже заметили, что намечается знакомая картинка. И ассоциация более, чем верная. Две волны накладываются друг на друга и получается более сложная волнообразная структура.

Но синусом мир не ограничивается. Никто не мешает поскладывать и другие функции. И поумножать тоже. И поделить. Для примера возьмем косинус и степенную функцию:

(x) => {    return 2 * Math.cos(3 * x) / Math.pow(x + 1, 2);}

Получилась штука, которую во фронтенде ассоциируют со словом bounce (зеленая на графике). Заготовка для анимаций, построенная подобным образом, часто используется и в CSS-библиотеках, и встречается во всех более-менее популярных JS библиотеках для анимаций.

Можно подумать, что зеленая кривая здесь отображает график колебания пружины, но это не совсем так. Просто очень похоже на нее. Настолько похоже, что пользователь скорее всего не заметит разницы.

Но к вопросам физики мы еще вернемся.

Промежуточные итоги

Прежде, чем идти дальше, отметим самое важное, что нужно запомнить:

• Графики функций вида y = f(x) можно использовать как траектории для анимаций.
• Коэффициенты позволяют подвинуть траекторию в нужное место и растянуть до нужного размера.
• Иногда можно сымитировать физический процесс с достаточной точностью путем сочетания простых функций.

II. Полярная система координат

Переход из одной системы координат в другую часто может сделать что-то сложное чем-то простым, либо напротив что-то очень простое превратить во что-то, ломающее мозг. Полярная система координат не очень часто встречается в работе верстальщика, так что у многих возникают сложности с ее пониманием. И действительно, мы привыкли задавать положение чего-то в виде координат (X, Y), а здесь нужно брать угол (направление) и радиус (расстояние) до точки. Это очень непривычно.

В целом связь между координатами (X, Y) и (R, ) простая, но от этого само преобразование не становится очевидным:

const x = r * Math.cos(p);const y = r * Math.sin(p);

Здесь и дальше мы будем использовать букву p вместо стандартной , чтобы примеры кода не наполнялись unicode-символами.

На пальцах разница между полярной и прямоугольной системами координат примерно такая же, как между выражением идите отсюда 5 километров на северо-восток, а там увидите и вот вам GPS-координаты по широте и долготе.

На самом деле самый толковый способ понять, как все это работает это посмотреть на практике, чем мы и займемся.

Возьмем простую функцию:

(p) => {    return p / 5;}

Она будет теперь отображать зависимость расстояния от направления, от угла (в радианах), который это направление задает. Постепенно увеличивая угол мы будем крутиться, как маленький человечек на стрелке на часах, и дальше останется рисовать линию там, где мы едем. Если бы функция каждый раз возвращала одно и то же значение, то длина стрелки бы не менялась, а мы бы рисовали окружность. Но наша функция дает прямую зависимость расстояния от угла, соответственно стрелка становится все длиннее, мы уезжаем дальше от центра и радиус круга, который мы рисуем, увеличивается. Получается спираль.

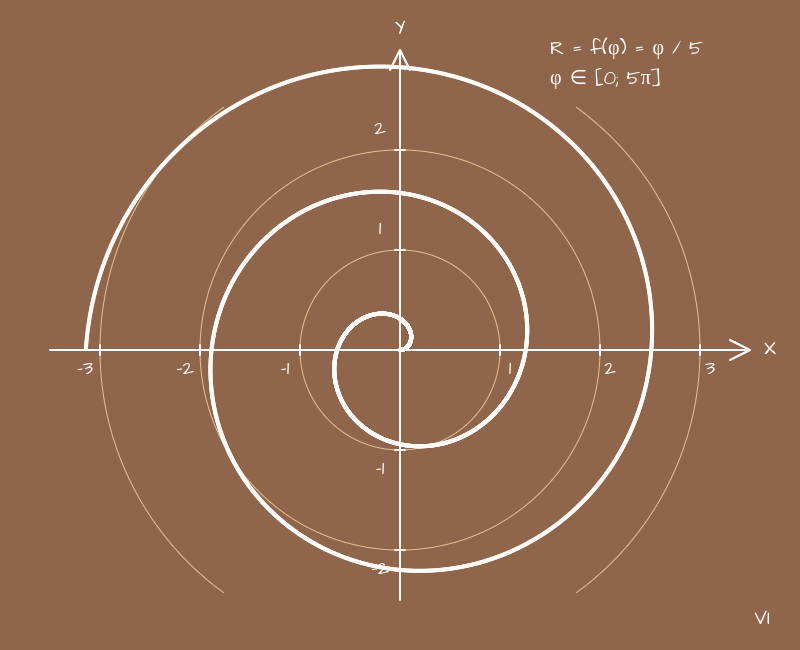
Но линейные зависимости это слишком скучно. Вернем нашу синусоиду на место и нарисуем ее одновременно в декартовой системе координат, используя как зависимость Y от X, и в полярной, как зависимость расстояния от угла.

Стоп. Что? Именно такая мысль должна здесь вас посетить. Почему синусоида стала круглой? Может даже показаться, что здесь что-то нечисто, что рисовалка графиков сломалась, но нет. Все так и должно быть. И на самом деле это небольшое наблюдение дает широкий простор для творчества.

Давайте произведем все те же манипуляции с коэффициентами, что мы делали с функциями в самом начале, и посмотрим, как они влияют на графики в полярной системе координат.

(p) => {    return Math.sin(5 * p);}(p) => {    return 2 * Math.sin(5 * p + 1);}

Цветочки! Конечно, что же еще здесь могло получиться?

Очень полезно воспользоваться одной из множества рисовалок графиков в сети и поэкспериментировать с разными функциями и коэфффициентами самостоятельно. Личный опыт в таких вопросах всегда дает лучшее понимание происходящего, чем отдельно взятые примеры от других людей.

Можно заметить, что теперь коэффициенты работают немного по-другому. Коэффициенты при параметре функции (теперь это угол) вращают график по кругу, а при всей функции растягивают его от центра.

Можно также заметить, что количество лепестков связано с коэффициентом при угле, так что очень легко делать цветочки с разным количеством лепестков.

Продолжим:

(p) => {    return Math.sin(p) + 0.2 * Math.sin(2 * p);}(p) => {    return 2 * Math.sin(p) + 0.2 * Math.sin(10 * p);}(p) => {    return Math.sin(3 * p - Math.PI / 2) * Math.sin(4 * p);}

Человечек! Начинает казаться, что комбинации графиков можно использовать как замену для пятен Роршаха.

Продолжая комбинировать функции мы получим своеобразные кляксы:

(p) => {    return (Math.sin(p) + Math.sin(p * 2) + 2) / 4;}(p) => {    return (Math.sin(p) + Math.sin(p * 3) + 2) / 2;}(p) => {    return Math.sin(p) + Math.sin(p * 4) + 2;}

Таким образом можно сделать вывод, что комбинируя функции и делая графики в полярной системе координат, мы можем с легкостью получать сложные циклические траектории, которые могут быть очень кстати, если нужно заставить какой-то объект в анимации колебаться у определенной точки или вокруг нее. При работе с абстрактной генеративной графикой стоит помнить о такой возможности.

Промежуточные итоги

Повторим некоторые моменты:

• Полярная система координат помогает строить сложные абстрактные траектории вокруг одной точки.
• Полезно экспериментировать с комбинациями функций и коэффициентов, чтобы при необходимости получить определенный характер движения, примерно знать, из чего можно сформировать нужную траекторию.

III. Параметрическое представление функций

Мы начали с использования функций вида y = f(x). Но мы также можем сделать x зависящим от чего-то еще. Это приведет к заданию координат в виде системы:

x = f1(t)y = f2(t)

В нашем случае это может быть очень кстати. Дело в том, что все предыдущие примеры были очень предсказуемыми, ограниченными. Мы не могли синусоиду развернуть, полетать туда-сюда или еще что-то такое сделать. Каждому x соответствовал один y. Ну или, в терминах полярной системы координат каждому углу соответствовал один радиус. С добавлением нового параметра мы снимаем эти ограничения.

В контексте анимаций подход с использованием дополнительного параметра органично вписывается в идею использовать в качестве этого параметра время. Или, если выражаться точнее, то локальное время с начала анимации. Идем по времени вперед анимация происходит в прямую сторону, идем по времени назад анимация проигрывается в обратную сторону. Это очень гибкий подход.

На самом деле мы можем представить все предыдущие примеры так, что была зависимость:

x = ty = f(t)

Или, в терминах кода, как вариант:

x: (t) => {    return t;},y: (t) => {    return (t / 2) - 1;}

Наши простые прямые выглядели бы как-то так:

Это было бы усложнением примеров на ровном месте, т.к. параметр t не играл бы никакой практической роли, мы меняли координату x напрямую, но дальше мы будем его везде подразумевать.

Сейчас мы не будем подробно останавливаться на этом вопросе, но отметим, что некоторые стандартные геометрические фигуры можно легко получить именно используя параметрическое представление:

Полезно об этом помнить.

Что будет, если мы возьмем для разнообразия косинус, и модуль от него? Получится что-то похожее на траекторию полета подпрыгивающего резинового мячика. Но реальный мячик будет подпрыгивать все меньше и меньше. Мы можем попытаться выразить изменения в движении по каждой из координат (X, Y) в виде отдельных функций, используя опыт, полученный ранее из экспериментов с ними. Вариантов там будет бесконечно много, но допустим наугад получилось что-то такое:

x: (t) => {    return 5 * t / (t + 1);},y: (t) => {    return 2 * Math.abs(Math.cos(5 * t)) / (t*t + 1);}

Что будет выглядеть как-то так:

Мы попытались угадать комбинации простейших функций, которые бы дали в результате что-то похожее на подпрыгивание мячика. Но насколько это на самом деле похоже на него? Можем ли мы вообще вот так взять и угадать траекторию такого сложного с точки зрения физики движения?

На самом деле вот так по графику мы не сможем оценить субъективную реалистичность движения, его нужно будет посмотреть в динамике. Но я вам скажу по секрету, что это не будет похоже на настоящее подпрыгивание. Ну то есть если мы запустим точку летать по этой траектории, то формально это подойдет под описание подпрыгивающего объекта, но где-то глубоко в подсознании будет казаться, что что-то здесь не так, что движение неестественное. Да, оно похоже на то, что нужно, но не совсем. Все же физические законы и наша попытка угадать их это не одно и то же. Отсюда можно сделать важное замечание:

Если у вас в проекте нужны достаточно реалистичные движения не гадайте, а возьмите готовые формулы из учебника физики.

Давайте попробуем это сделать на примере все этого же мячика.

Немного физики

Как только мы откроем учебник, нас встретят формулы для скорости и положения тела в зависимости от времени. Ну и также в них есть сопуствующие коэффициенты вроде ускорения свободного падения.

Мы сразу обнаружим, что нельзя так просто посчитать всю траекторию сразу, нам нужно находить моменты падения и считать каждое подпрыгивание по отдельности. Это мгновенно приведет к увеличению кодовой базы и перестанет быть похожим на простую математическую функцию:

x: (t) => {    return t;},y: (() => {    let y0 = 2;     // Изначальное положение по Y    let v0 = 0;     // Изначальная скорость    let localT = 0; // Локальное время полета от последнего отскока    let g = 10;     // Ускорение свободного падения    let k = 0.8;    // Условный коэффициент для не совсем упругого отскока    return (t) => {        let y = y0 + v0 * localT - g * localT * localT / 2;        if (y <= 0) {            y = 0;            y0 = 0;            v0 = (-v0 + g * localT) * k;            localT = 0;        }        localT += 0.005;        return y;    };})()

Но зато результат будет и более реалистичным, и более практичным в плане адаптации его под разные условия использования.

Удобство здесь вещь не самая бесполезная. Обратите внимание, как меняется график, когда мы меняем коэффициенты. Пусть ускорение свободного падения станет равным 1.62, как на Луне. Что произойдет? Траектория сохранила характер, но условный мячик теперь дольше висит в воздухе после каждого подпрыгивания. Или поменяем коэффициент, условно определяющий насколько упругое отталкивание происходит и у нас уже не резиновый мячик, а деревянный карандаш. Стандартные формулы дают предсказуемое поведение при изменении отдельных коэффициентов. Если бы мы имели чисто на глазок угаданную закономерность, было бы очень сложно ее адаптировать таким же образом, особенно при редактировании кода, написанного несколько лет назад.

Такая проблема часто встречается в разных экспериментальных примерах с CodePen, когда оригинальный автор угадал что-то под свою задачу, сильно похожую на нашу, и мы попадаем в ловушку, говоря да там работы на пару минут, сейчас все будет двигаться как нужно, а потом, спустя час, решаем, что переписать это решение проще, чем доработать. Будьте внимательны!

В качестве упражнения вы можете попробовать смоделировать аналогичное падение мячика, но уже по наклонной поверхности, это может быть хорошей практикой по этой теме.

Подобные относительно сложные с точки зрения физики процессы, связанные с кинематикой, магнетизмом или моделированием жидкостей редко встречаются в обычной верстке. Здесь, конечно, речь идет о дизайнерских сайтах с генеративной графикой или какими-то интерактивными физическими моделями. Но тем не менее, если вы стремитесь развиваться в своей области это может быть неплохой темой для ознакомления на пару вечеров. Специалистом по моделированию физических процессов вы не станете, но кругозор в вопросах анимирования расширится, а это очень здорово. Когда встанет задача сделать что-то с этими темами связанное, вы уже будете знать, куда смотреть.

Промежуточные итоги

На последних примерах мы увидели следующее:

• Время в анимациях можно использовать в качестве параметра в параметрическом представлении функций. Да и в целом привязывать анимацию ко времени удобно.
• При использовании параметрического представления функций у нас нет ограничений вида одному X соответствует один Y. Можно усложнить траектории.
• Параметрическое представление подталкивает к моделированию физических процессов, но, если вам нужна реалистичность и универсальность имеет смысл запастить справочником по физике и брать готовые формулы оттуда.

IV. Кривые Безье

С кривыми Безье сталкивался, наверное, каждый верстальщик. Мы их постоянно используем в CSS. Но на самом деле то, что мы там используем это очень частный случай их применения. Мы же посмотрим на все это в более общем случае.

Если пойти на википедию и почитать о том, что же такое кривая Безье, то мы увидим страшные формулы с большим знаком суммы, который так и отдает высшей матиматикой и всех пугает. Но можно это все сформулировать на пальцах.

У нас есть набор точек. Две. Три. Пять. Десять. Сколько угодно. Для этих точек по определенной закономерности строятся выражения, которые мы потом складываем в одно и получаем супер-мега-параметрическую функцию, где координаты этих точек играют роль коэффициентов.

В зависимости от количества точек кривая будет иметь соответствующее название. Кубическая кривая безье будет иметь 4 точки, а наш параметр t (в контексте анимаций время) будет максимум в третьей степени поэтому она и кубическая. Если будет больше точек, то степени будут увеличиваться. Это все приведет к увеличению нагрузки на процессор, снижению производительности в большинстве случаев, и широкое практическое применение имеют только кубические кривые Безье. В CSS используются именно они. А еще они используются в SVG для создания path. Но об этом чуть дальше.

Здесь стоит сказать, что чем больше точек, тем более сложную кривую можно построить. Из двух точек получится просто прямая. Из трех дуга (возможно ассимметричная). Из четырех загогулька в виде буквы S, либо дуга с двойным перегибом. Из пяти загогулька с еще одним перегибом, и.т.д.

Но вернемся к четырем точкам, пропустим все расчеты и сразу перейдем к нужной нам форме двум функциям для X и Y от t:

x: (t) => {    return ((1-t)*(1-t)*(1-t)*x0) + (3*(1-t)*(1-t)*t*x1) + (3*(1-t)*t*t*x2) + (t*t*t*x3);},y: (t) => {    return ((1-t)*(1-t)*(1-t)*y0) + (3*(1-t)*(1-t)*t*y1) + (3*(1-t)*t*t*y2) + (t*t*t*y3);}

Здесь (x0, y0) координаты первой точки, (x1, y1) второй и.т.д. Они, как мы уже отметили, выполняют роль коэффициентов.

Давайте построим график, взяв первую точку в координатах (0, 0), а последнюю, четвертую, в (1, 1). Для удобства первая и вторая, а также третья и четвертая точки будут соединяться отрезками, чтобы было понятно, в каком порядке они идут.

На графике можно заметить, что меняя параметр t от 0 до 1 мы получаем знакомую кривую, вписанную в квадрат, которую мы привыкли видеть в CSS. Это она и есть.

Вы можете спросить, а зачем так все усложнять? Та кривая на картинке это же почти график корня x, неужели нельзя ее получить более простым способом?

Все дело в том, что это очень частный случай. Мы не обязаны фиксировать точки в координатах (0, 0) или (1, 1). Мы можем брать вообще любые точки. Что, собственно, и сделаем:

Как вы можете видеть, получаемые траектории плавные, могут самопересекаться, и, что самое главное прогнозируемые. Немного экспериментов и вы будете четко понимать, куда пойдет кривая, если подвинуть ту или иную точку. Это очень удобно.

Вы можете также обратить внимание, что график начинает идти точками. Это особенность работы конкретной программы, но это не баг, а фича. Расстояние во времени (параметре t в нашем случае) между точками одинаковое. Эти графики строятся по принципу мячика, оставляющего след, о котором мы говорили в самом начале. Этот пунктир показывает, где анимация будет идти быстрее, где скорость движения увеличится. В поворотах скорость меньше, на относительно прямых участках больше. Это добавляет определенную физику в движение, делает его более разнообразным, что часто бывает очень кстати.

Такого рода кривые хорошо использовать при анимациях появления или улетания объектов.

Но что-то мы совсем забыли о синусе. Почему бы его не добавить к имеющимся выражениям?

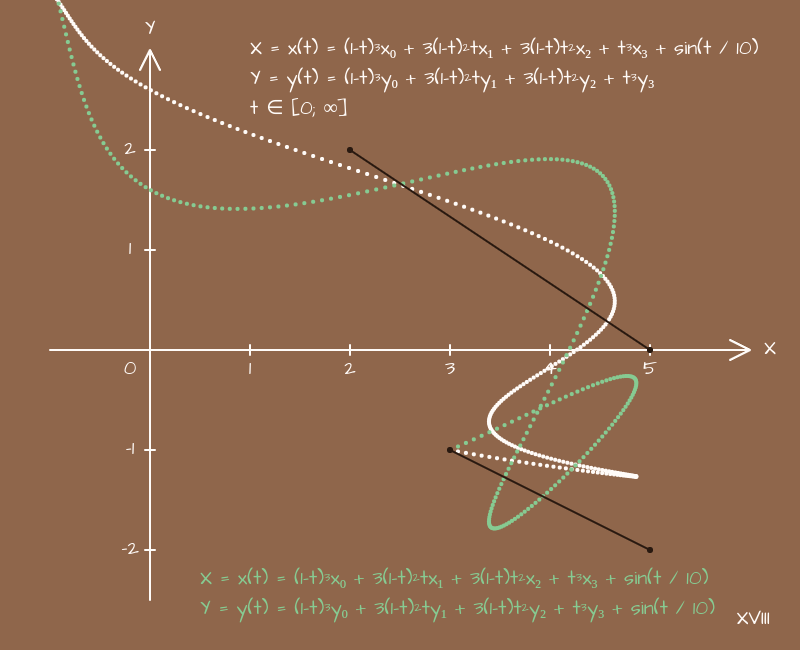
Ооо Небольшой шум в виде синуса делает траекторию менее предсказуемой, но с другой стороны она сохраняет общее направление и стала даже более интересной. Полезно это запомнить.

Последовательности кривых Безье

В примере с мячиком мы уже столкнулись с сочетанием нескольких функций. Движение идет сначала по одной, потом по другой и.т.д. Мы можем сочетать все, что угодно, но наверное самые интереные и полезные результаты будут, если начать комбинировать кривые Безье. В SVG именно последовательности этих кривых используются для того, чтобы делать path сложной формы. Там, конечно, они разбавляются еще прямыми, получается более запутанная структура, но общий смысл мы постараемся воспроизвести.

У кривых Безье есть одна особенность, которая нам в этом поможет. Часть кривой, соответствующая значениям параметра от 0 до 1 начинается в первой точке и заканчивается в четверной (мы все еще говорим про кубические кривые). Этот факт позволяет ограничить траекторию, и мы будем точно знать, где она начнется, и где закончится.

А дальше самое интересное: если угол наклона отрезка между третьей и четвертой точками одной кривой и первой и второй точками у второй кривой будет одинаковым, то они сольются в одну. Там не будет стыка, острого угла, резкого перехода. А если их длина будет совпадать, то это сыграет нам на руку, нормализовав разницу в скорости движения, если мы будем использовать время как параметр в наших функциях.

Такое сочетание лучше посмотреть на картинке:

Здесь мы видим 4 кривых Безье, которые слились в одну. Если убрать вспомогательные точки и отрезки, то никто и не догадается, что это не одна кривая, а несколько.

Таким образом возможно на ходу делать плавные траектории, огибающие какие-то объекты на условной сцене, где происходит анимация.

Пусть точки, где кривые соединяются, будут называться опорными. Что будет, если эти опорные точки будут стоять на месте, а соседние с ними мы начнем двигать, симметрично относительно друг друга (если одна движется вверх вторая вниз, одна влево другая вправо)?

У нас получится набор кривых, схожих по направлению, но как бы слегка колеблющихся:

Это может быть хорошей базой для создания разного рода желейных эффектов, когда какой-то контур немного плавает туда-сюда, а в контексте траекторий можно сделать так, чтобы она каждый раз немного менялась, сохраняя свою плавность и общее направление движения. Иногда это очень полезно.

Промежуточные итоги

Давайте обобщим сказанное.

• Кривые Безье это очень мощный инструмент, позволяющий делать сложные, но предсказуемые траектории для абстрактных анимаций.
• Любые кривые можно соединить в более сложную траекторию, если проявить некоторую аккуратность.

Заключение

Не так страшен черт, как его малюют. Генерирование траекторий определенной формы для движений в покадровых анимациях кажется сложной задачей, но имея общие представления о том, что можно делать с графиками функций, она становится вполне доступной. Дальше останется только вопрос оптимизаций, но он индивидуален для каждого проекта, да и редко на самом деле подобные функции становятся узким местом в производительности. Надеюсь, что данный набор иллюстраций поможет начинающим разработчикам составить представление о том, что можно делать, и где примерно искать ответы на свои вопросы, если встанет вопрос о сложных движениях в 2D анимациях.

В прошлый раз мы говорили о графиках и траекториях для покадровых анимаций, а сегодня речь пойдет про матрицы. Мы разберемся с тем, как строятся базовые трансформации в CSS, SVG и WebGL, построим отображение 3D-мира на экране своими руками, попутно проводя параллель с таким инструментом, как Three.js, а также поэкспериментируем с фильтрами для фотографий и разберемся, что же за магия такая лежит в их основе.

Напомню, что в этой серии статей мы знакомимся с разными штуками из области математики, которые пугают верстальщиков, но могут быть полезны при решении рабочих задач. Мы стараемся избежать излишней теоретизации, отдавая предпочтение картинкам и объяснению на пальцах, с акцентом на практическое применение во фронтенде. В связи с этим формулировки местами могут быть не совсем точными с точки зрения математики, или не совсем полными. Цель этой статьи дать общее представление о том, что бывает, и откуда можно начать в случае чего.

Скрипты для генерирования картинок в стиле этого цикла статей находятся на GitHub, так что если если вы хотите себе сообразить такие же вы знаете что делать.

Немного определений

Матрица в математике это такая абстракция, можно сказать, что это тип данных в каком-то смысле, и записываетя она в виде прямоугольной таблицы. Количество столбцов и строк может быть любым, но в вебе мы почти всегда имеем дело с квадратными матрицами 2x2, 3x3, 4x4, и 5x5.

Также нам понадобится такое определение, как вектор. Думаю из школьной геометрии вы можете вспомнить определение, связанное со словами длина и направление, но вообще в математике вектором может называться очень много чего. В частности мы будем говорить о векторе, как об упорядоченном наборе значений. Например координаты вида (x, y) или (x, y, z), или цвет в формате (r, g, b) или (h, s, l, a) и.т.д. В зависимости от того, сколько элементов вошло в такой набор мы будем говорить о векторе той или иной размерности: если два элемента двумерный, три трехмерный и.т.д. Также, в рамках рассматриваемых тем, может быть удобно иногда думать о векторе, как о матрице размера 1x2, 1x3, 1x4 и.т.д. Технически можно было бы ограничиться только термином матрица, но мы все же будем использовать слово вектор, чтобы отделить эти два понятия друг от друга, хотя бы в логическом смысле.

Для матриц, равно как и для векторов, определены разные операции, которые с ними можно делать. В частности умножение. Мы постоянно их умножаем между собой. Сам алгоритм умножения не очень сложный, хотя может показаться немного запутанным:

function multiplyMatrices(a, b) {    const m = new Array(a.length);    for (let row = 0; row < a.length; row++) {        m[row] = new Array(b[0].length);        for (let column = 0; column < b[0].length; column++) {            m[row][column] = 0;            for (let i = 0; i < a[0].length; i++) {                m[row][column] += a[row][i] * b[i][column];            }        }    }    return m;}

Но для нас на самом деле не так важно постоянно помнить принцип его работы при решении бытовых задач. Здесь мы упоминаем его скорее для полноты картины, чтобы внести контекст в дальнейшие примеры.

При работе со сложными сущностями в математике очень полезно абстрагироваться. Как здесь мы будем часто говорить про умножение, но не будем уделять внимание тому, какие именно арифметические операции в каком порядке там происходят. Мы знаем, что умножение определено и этого достаточно для работы.

Мы будем использовать только квадратные матрицы в очень частном наборе задач, так что будет достаточно набора простых правил:

• Умножать можно только матрицы одной размерности.
• Умножаем матрицу на матрицу получаем матрицу.
• Можно умножить матрицу на вектор получим вектор.
• Порядок умножения важен.

Мы будем использовать в основном запись умножения слева направо, как более привычную и подходящую для объяснений, но в некоторых книгах или библиотеках вы можете встретить запись справа налево, а все матрицы будут зеркально отражены по диагонали. Это никак не влияет на суть происходящих манипуляций, так что мы не будем на этом зацикливаться, но если будете что-то копипастить обращайте внимание.

Также для дальнейшей работы нам понадобится такое понятие, как единичная матрица. Это матрица, у которой по главной диагонали расположены единицы, а во всех остальных ячейках нули. Алгоритм умножения построен таким образом, что умножая единичную матрицу на другую матрицу получаем ту самую матрицу. Или вектор, если мы говорим о векторе. Иными словами единичная матрица выполняет роль единицы при обычном умножении чисел. Это нейтральная штука, которая при умножении ни на что не влияет.



И последнее, что нам понадобится, это пример, показанный на картинке выше. Это как бы частный случай умножения матрицы на вектор, когда у матрицы последняя строка представляет собой кусочек единичной матрицы, а у вектора последний элемент тоже равен 1.

В этом примере мы используем буквы (x, y), и как вы уже можете догадаться, дальше речь пойдет о координатах в 2D. Но зачем добавлять третью координату и оставлять ее единицей? спросите вы. Все дело в удобстве, или даже лучше сказать, что в универсальности. Мы очень часто добавляем +1 координату для упрощения расчетов, и работа с 2D идет с матрицами 3x3, работа с 3D с матрицами 4x4, а работа с 4D, например с цветами в формате (r, g, b, a) идет с матрицами 5x5. На первый взгляд это кажется безумной идеей, но дальше мы увидим, насколько это унифицирует все операции. Если вы захотите более подробно разобраться в этой теме, то можете загуглить выражение однородные координаты.

Но довольно теории, перейдем к практике.

I. Базовые трансформации в компьютерной графике

Давайте возьмем выражения из упомянутого примера и посмотрим на них как есть, вне контекста матриц:

newX = a*x + b*y + cnewY = d*x + e*y + f

Можно рассматривать это как параметрические уравнения, графики которых мы строили в прошлый раз. Что будет, если задать те или иные коэффициенты в них? Начнем со следующего варианта:

newX = 1*x + 0*y + 0 = xnewY = 0*x + 1*y + 0 = y

Здесь ничего не меняется новые координаты (x, y) идентичны старым. Если подставить эти коэффициенты в матрицу и внимательно присмотреться, то увидим, что получится единичная матрица.

А что получится, если взять другие коэффициенты? Например вот такие:

newX = 1*x + 0*y + A = x + AnewY = 0*x + 1*y + 0 = y

Мы получим смещение по оси X. Впрочем, что еще здесь могло получиться? Если для вас это не очевидно, то лучше вернуться к первой части, где мы говорили про графики и коэффициенты.

Меняя эти 6 коэффициентов a, b, c, d, e, f и наблюдая за изменениями x и y, рано или поздно мы придем к четырем их комбинациям, которые кажутся полезными и удобными для практического применения. Запишем их сразу в форме матриц, возвращаясь к изначальному примеру:



Названия этих матриц говорят сами за себя. При умножении этих матриц на вектора с координатами каких-то точек, объектов на сцене и.т.д. мы получаем новые координаты для них. Причем оперируем мы интуитивно понятными трансформациями перемещение, масштабирование, поворот и наклон, а коэффициенты определяют выраженность той или иной трансформации по соответствующим осям.

Очень часто удобно воспринимать матрицы именно как трансформации для чего-либо, например для координат. Это еще раз к слову об абстракциях.

Трансформации можно складывать. В терминах матриц мы будем использовать операцию умножения, что может немного путать, но это издержки разговорного языка. Если нам нужно какой-то объект сместить в сторону и увеличить, то мы можем взять матрицу для смещения, матрицу для масштабирования, и перемножить их. Результат будет представлять из себя матрицу, которая дает и смещение, и масштабирование одновременно. Останется только каждую точку нашего объекта подвергнуть трансформации с ее помощью.

Базовые трансформации в CSS

Но это все слова. Давайте посмотрим, как это выглядит в реальном фронтенде. В CSS у нас (внезапно) есть функция matrix. Выглядит она в контексте кода как-то так:

.example {    transform: matrix(1, 0, 0, 1, 0, 0);}

Многих новичков, которые впервые видят ее, накрывает вопрос почему здесь шесть параметров? Это странно. Было бы 4 или 16 еще куда не шло, но 6? Что они делают?

Но на самом деле все просто. Эти шесть параметров те самые коэффициенты, из которых мы только что собирали матрицы для базовых трансформаций. Только их почему-то расставили в другом порядке:



Также в CSS есть функция matrix3d для того, чтобы задавать с помощью матрицы трансформацию в 3D. Там уже есть 16 параметров, ровно чтобы сделать матрицу 4x4 (не забываем, что мы добавляем +1 размерность).

Матрицы для базовых 3D трансформаций строятся так же, как и для 2D, только нужно больше коэффициентов, чтобы расставлять их не по двум координатам, а по трем. Но принципы те же.

Естественно, каждый раз городить матрицу и следить за корректной расстановкой коэффициентов при работе с простыми трансформациями в CSS было бы странно. Мы, программисты, обычно все же стараемся упростить себе жизнь. Так что у нас в CSS появились краткие функции для создания отдельных трансформаций translateX, translateY, scaleX и.т.д. Обычно мы используем именно их, но важно понимать, что внутри они создают эти же самые матрицы, о которых мы говорили, просто скрывая от нас этот процесс за еще одним слоем абстракции.

Эти же самые трансформации translate, rotate, scale и skew, а также универсальная функция matrix для задания трансформаций, присутствуют и в SVG. Синтаксис немного другой, но суть такая же. При работе с трехмерной графикой, например с WebGL, мы тоже будем прибегать к этим же трансформациям. Но об этом чуть позже, сейчас важно понять, что они есть везде, и работают везде по одному и тому же принципу.

Промежуточные итоги

Обобщим вышесказанное:

• Матрицы могут быть использованы в качестве трансформаций для векторов, в частности для координат каких-то объектов на странице.
• Почти всегда мы оперируем квадратными матрицами и добавляем +1 размерность для упрощения и унификации вычислений.
• Есть 4 базовых трансформации translate, rotate, scale и skew. Они используются везде от CSS до WebGL и везде работают схожим образом.

II. Построение 3D сцены своими руками

Логичным развитием темы про трансформации координат будет построение 3D сцены и отображение ее на экране. В той или иной форме эта задача обычно есть во всех курсах по компьютерной графике, но вот в курсах по фронтенду ее обычно нет. Мы посмотрим может быть немного упрощенный, но тем не менее полноценный вариант того, как можно сделать камеру с разными углами обзора, какие операции нужны, чтобы посчитать координаты всех объектов на экране и построить картинку, а также проведем параллели с Three.js самым популярным инструментом для работы с WebGL.

Здесь должен возникнуть резонный вопрос зачееем? Зачем учиться делать все руками, если есть готовый инструмент? Ответ кроется в вопросах производительности. Вероятно вы бывали на сайтах с конкурсами вроде Awwwards, CSS Design Awards, FWA и им подобных. Вспомните, насколько производительные сайты принимают участие в этих конкурсах? Да там почти все тормозят, лагают при загрузке и заставляют ноутбук гудеть как самолет! Да, конечно, основная причина обычно это сложные шейдеры или слишком большое количество манипуляций с DOM, но вторая невероятное количество скриптов. Это катастрофическим образом влияет на загрузку подобных сайтов. Обычно все происходит так: нужно сделать что-то на WebGL берут какой-нибудь 3D движок (+500КБ) и немного плагинов для него (+500КБ); нужно сделать падение объекта или разлетание чего-то берут физический движок (+1МБ, а то и больше); нужно обновить какие-то данные на странице ну так добавляют какой-нибудь SPA-фреймворк с десятком плагинов (+500КБ) и.т.д. И таким образом набирается несколько мегабайтов скриптов, которые мало того, что нужно загрузить клиенту (и это еще вдобавок к большим картинкам), так еще и браузер с ними что-то будет делать после загрузки они же не просто так к нему прилетают. Причем, в 99% случаев, пока скрипты не отработают, пользователь не увидит всей той красоты, которую ему бы нужно с самого начала показывать.

Народная примета гласит, что каждые 666КБ скриптов в продакшене увеличивают время загрузки страницы на время, достаточное, чтобы пользователь отправил разработчика сайта на следующий круг ада. Three.js в минимальной комплектации весит 628КБ...

При этом часто задачи просто не требуют подключения сложных инструментов. Например чтобы показать пару плоскостей с текстурами в WebGL и добавить пару шейдеров, чтобы картинки расходились волнами, не нужен весь Three.js. А чтобы сделать падение какого-то объекта не нужен полноценный физический движок. Да, он скорее всего ускорит работу, особенно если вы с ним знакомы, но вы заплатите за это временем пользователей. Тут каждый решает сам для себя, что ему выгоднее.

Цепочка преобразований координат

На самом деле суть преобразований координат для построения 3D-сцены у себя на экране довольно простая, но мы все же разберем ее по шагам, т.к. скорее всего для многих верстальщиков этот процесс будет чем-то новым.

Так вот. Допустим дизайнер нарисовал 3D-модель. Пусть это будет куб (в примерах будем использовать максимально простые построения, чтобы не усложнять иллюстрации на ровном месте):



Что эта модель из себя представляет? По сути это набор точек в какой-то системе координат и набор взаимосвязей между ними, чтобы можно было определить, между какими из точек должны находиться плоскости. Вопрос плоскостей в контексте WebGL будет лежать на плечах самого браузера, а для нас важны координаты. Нужно понять, как именно их преобразовать.

У модели, как мы и сказали, есть система координат. Но обычно мы хотим иметь много моделей, хотим сделать сцену с ними. Сцена, наш 3D-мир, будет иметь свою, глобальную систему координат. Если мы просто будем интерпретировать координаты модели как глобальные координаты то наша модель будет находиться как бы в центре мира. Иными словами, ничего не поменяется. Но мы хотим добавить много моделей в разные места нашего мира, примерно так:



Что же делать? Нужно преобразовать координаты каждой отдельной модели в глобальные координаты. Расположение модели в пространстве задается смещениями, поворотами и масштабированием мы уже видели эти базовые трансформации. Сейчас нам нужно для каждой модели построить матрицу трансформаций, которая будет хранить в себе как раз эту информацию о том, где находится модель относительно мира, и как повернута.

Например для кубиков будут примерно такие матрицы:

// Центральный кубик в центре мира.// Единичная матрица ничего не меняет и координаты просто интерпретируются как глобальные.const modelMatrix1 = [    [1, 0, 0, 0],    [0, 1, 0, 0],    [0, 0, 1, 0],    [0, 0, 0, 1]];// Кубик, смещенный по глобальной оси X.const modelMatrix2 = [    [1, 0, 0, 1.5],    [0, 1, 0, 0  ],    [0, 0, 1, 0  ],    [0, 0, 0, 1  ]];// Кубик, смещенный по глобальной оси X в другую сторону.const modelMatrix3 = [    [1, 0, 0, -1.5],    [0, 1, 0, 0   ],    [0, 0, 1, 0   ],    [0, 0, 0, 1   ]];

Дальше мы будем действовать примерно следующим образом:

для каждой точки модели {    глобальные координаты точки = [ матрица этой модели ] * локальные кординаты}

Соответственно для каждой модели нужна своя матрица.

Аналогичным образом можно делать цепочку из каких-то объектов. Если птица должна махать крыльями, то будет уместно координаты точек крыла сначала перевести в координаты птицы, а потом уже в глобальные мировые координаты. Это будет куда проще угадывания траектории крыла сразу в глобальных координатах. Но это так, к слову.

Дальше нужно определиться с тем, с какой стороны мы будем смотреть на мир. Нужна камера.



Камера это такая абстракция, как бы имитация физической камеры. У нее есть координаты и какие-то углы наклона, задающие ее расположение в глобальных координатах. Наша задача преобразовать набор теперь уже глобальных координат в систему координат камеры. Принцип тот же, что и в предыдущем примере:

для каждой точки в мире {    координаты точки для камеры = [ матрица камеры ] * глобальные кординаты}

Если у вас сложная сцена, то будет иметь смысл произвести некоторые оптимизации и не считать ничего для точек, которые точно не попадут в поле зрения камеры. Не забывайте о производительности!

Давайте посмотрим на сцену с того места, где стоит наша условная камера:



Сейчас, преобразовав все точки в систему координат камеры, мы можем просто выбросить ось Z, а оси X и Y интерпретировать как горизонтальную и вертикальную. Если нарисовать все точки моделей на экране, то получится картинка, как в примере никакой перспективы и сложно понять, какая часть сцены на самом деле попадает в кадр. Камера как бы бесконечного размера во все стороны. Мы можем как-то все подогнать, чтобы то, что нужно, влезло на экран, но было бы неплохо иметь универсальный способ определения того, какая часть сцены попадет в поле зрения камеры, а какая нет.

У физических камер мы можем говорить о такой штуке, как угол обзора. Почему бы и здесь его не добавить?

Для этого нам понадобится еще одна матрица матрица проекции. Вообще строить ее можно по-разному. В зависимости от того, что взято за изначальные параметры, получится немного разный вид этой самой матрицы, но суть будет одна и та же. Мы возьмем следующий, немного упрощенный вариант:

// Пусть угол обзора будет 90 градусовconst s = 1 / (Math.tan(90 * Math.PI / 360));const n = 0.001;const f = 10;const projectionMatrix  = [    [s, 0, 0,          0],    [0, s, 0,          0],    [0, 0, -(f)/(f-n), -f*n/(f-n)],    [0, 0, -1,         0]];

Матрица проекции, так или иначе, содержит в себе три параметра это угол обзора, а также минимальное и максимальное расстояние до точек, с которыми идет работа. Выражаться это может по-разному, использоваться тоже по-разному, но эти параметры будут в этой метрице в любом случае.

Понимаю, что ни разу не очевидно, почему матрица выглядит именно так, но для ее выведения с пояснениями понадобится формул на 2-3 страницы. Это еще раз возвращает нас к мысли, что абстрагироваться полезно мы можем оперировать более общим результатом, не вдаваясь в мелкие детали там, где это не нужно для решения конкретной задачи.

Теперь, произведя уже знакомые преобразования:

для каждой точки в системе координат камеры {    координаты точки = [ матрица проекции ] * координаты в камере}

Получим в нашем поле зрения именно то, что и ожидаем. Увеличивая угол видим больше всего по сторонам, уменьшая угол видим только то, что ближе к направлению, куда камера направлена. PROFIT!



Но на самом деле нет. Мы забыли про перспективу. Бесперспективная картинка нужна мало где, так что нужно ее как-то добавить. И здесь, внезапно, нам не нужны матрицы. Задача выглядит очень сложной, но решается банальным делением координат X и Y на W для каждой точки:



* Здесь мы сместили камеру в сторону, и добавили параллельные линии на полу, чтобы было понятнее, где эта самая перспектива появляется.

Подбирая коэффициенты на свой вкус получим разные варианты перспективы. В каком-то смысле коэффициенты здесь определяют тип объектива, насколько он плющит окружающее пространство.

Теперь мы имеем полноценную картинку. Можно брать координаты X и Y для каждой точки и рисовать ее на экране любым удобным вам способом.

Вообще этого достаточно, чтобы построить сцену, но в реальных проектах вы также можете столкнуться с дополнительной трансформацией, связанной с масштабированием, в самом конце. Идея в том, что после проекции мы получаем координаты (x, y) в пределах 1, нормализованные координаты, а потом уже умножаем их на размер экрана или канваса, получая координаты для отображения на экране. Этот дополнительный шаг выносит размер канваса из всех вычислений, оставляя его только в самом конце. Иногда это удобно.

Здесь у вас, вероятно заболела голова от количества информации, так что притормозим и повторим еще раз все трансформации в одном месте:



Если эти трансформации объединить в одну, то получится паровозик.

Как это выглядит в Three.js?

Теперь, когда мы понимаем, откуда этот паровозик взялся, посмотрим на пример вершинного шейдера по умолчанию в Three.js, который ничего не делает:

void main() {    gl_Position = projectionMatrix * modelViewMatrix * vec4(position, 1.0);}

или в более полном варианте:

void main() {    gl_Position = projectionMatrix * viewMatrix * modelMatrix * vec4(position, 1.0);}

Ничего он вам не напоминает? Да, это именно этот паровозик. И под ничего не делает мы подразумеваем, что он как раз делает всю работу по пересчету координат, на основе заботливо переданных со стороны Three.js матриц. Но никто не мешает эти матрицы сделать своими руками, не так ли?

Типы камер в компьютерной графике и Three.js

Тема типов камер не касается непосредственно матриц, но все же уделим ей пару минут, раз уж все равно зашла речь про Three.js, а то порой у людей каша в голове по этому поводу.

Камера это абстракция. Она помогает нам мыслить в 3D мире таким же образом, как мы мыслим в мире реальном. Как мы уже сказали, у камеры есть положение в пространстве, направление, куда она смотрит, и угол обзора. Все это задается с помощью двух матриц и, возможно, дополнительного деления координат для создания перспекивы.

В компьютерной графике мы имеем два вида камер это с перспективой и без перспективы. Это два принципиально разных типа камер в техническом плане, требующих разных действий для получения изображения. И все. Больше ничего нет. Все остальное это их комбинации, какие-то более сложные абстракции. Например в Three.js есть стерео-камера это не какой-то особый тип камеры в техническом плане, а просто абстракция две камеры, немного разнесенные в пространстве и расположенные под углом:



Для каждой половины экрана мы берем свою камеру и получается стерео-картинка. А CubeCamera это 6 обычных камер, расположенных с разных сторон от какой-то точки, не более того.

Что дальше?

Следующий шаг, после получения координат объектов, это определение того, какие объекты будут видны, а какие скроются за другими. В контексте WebGL это браузер сделает сам. Ну и останутся еще сопутствующие задачи вроде наложения текстур на них, расчет освещения по нормалям, тени, постобработка картинки, и.т.д. Но самую важную и сложную для понимания часть мы уже сделали. Это очень здорово. На самом деле многие генеративные штуки не нуждаются в этих самых текстурах и освещении, так что очень может быть, что полученных сейчас знаний будет достаточно для работы с ними.

Кстати, отбрасывание тени от какого-то объекта на плоскость есть ни что иное, как проекция этого объекта на эту самую плоскость под определенным углом с последующим смешением цветов. Процесс по своей сути очень похож на работу камеры, но там добавляется еще угол между плоскостью проекции и направлением взгляда.

Про текстуры и эффекты для картинок на WebGL, в том числе без библиотек, мы говорили в предыдущих статьях уже не раз. Вы можете обратиться к ним, если вам эта тема интересна. Таким образом, объединив все эти знания воедино, мы сможем строить полноценные красочные 3D-штуки своими руками.

Мы действительно можем строить полноценные 3D-сцены своими руками. Но все же здесь важно соблюдать баланс для простой генеративной графики или каких-то эффектов для картинок это будет хорошей идеей. Для сложных сцен может быть проще все же взять готовый инструмент, потому что свой по объему будет приближаться к тому же Three.js и мы ничего не выиграем при избавлении от него. А если вам нужно естественное освещение, мех, стекло, множественные отражения или еще что-то в этом духе, то из соображений производительности может иметь смысл отказаться от самой идеи рендерить что-то в реальном времени и заранее заготовить картинки с видами на сцену с разных сторон и уже их показывать пользователю. Мыслите шире, не зацикливайтесь на определенном подходе к решению задач.

Промежуточные итоги

Сейчас самое время обобщить вышесказанное, чтобы в голове появилось место для следующего варианта применения матриц.

Итак:

• Можно построить 3D мир и рассчитать координаты объектов на экране своими руками, используя паровозик из матриц.
• В 3D мире мы оперируем такой абстракцией, как камера. Она имеет расмоложение, направление и угол обзора. Все это задается с помощью все тех же матриц. И есть два базовых вида камер с перспективой и без перспективы.
• В контексте WebGL ручное построение картинки на экране или физические расчеты часто позволяют выбросить тяжелые зависимости и ускорить загрузку страниц. Но важно соблюдать баланс между своими скриптами, готовыми инструментами, а также альтернативными вариантами решения задач, уделяя внимание не только своему удобству, но и вопросам скорости загрузки и конечной производительности, в том числе на телефонах.

III. Фильтры для изображений

Напоследок мы рассмотрим такую область применения матриц, как фильтры для изображений. Если мы рассмотрим цвет в формате RGBA как вектор, то можно предположить, что здесь можно применить трансформацию, аналогичную той, что мы использовали с координатами:



И применить это для картинки по очевидному принципу:

для каждого пикселя картинки {    новый цвет пикселя = [ фильтр ] * старый цвет пикселя}

Если в качестве матрицы будет выступать единичная матрица ничего не изменится, это мы уже знаем. А что будет, если применить фильтры, схожие с трансформациями translate и scale?



Оу. Получились фильтры яркости и контраста. Занятно.

При экспериментах с такими фильтрами всегда следует помнить о коррекция значений, чтобы изображение не засвечивалось. Если вы что-то умножаете на большое число скорее всего нужно где-то что-то вычесть или поделить. Что и было показано в предыдущем примере.

А как сделать черно-белое изображение из цветного? Первое, что может прийти в голову это сложить значения каналов RGB, поделить на 3, и использовать полученное значение для всех трех каналов. В формате матрицы это будет выглядеть как-то так:



И хотя у нас действительно получилось черно-белое изображение, его все еще можно улучшить. Наш глаз на самом деле по-разному воспринимает светлость разных цветов. И для того, чтобы как-то это передать при обесцвечивании, мы делаем разные коэффициенты для каждого канала RGB в этой матрице.

В примере ниже будут представлены общепринятые значения для этих коэффициентов, но никто не мешает с ними поиграть. В сумме эти коэффициенты должны давать 1, но в зависимости от их пропорций мы получим немного разные черно-белые изображения. Это может в какой-то степени имитировать разную цветопередачу при работе с пленочными фотоаппаратами.

А если мы еще и домножим главную диагональ немного, то получится универсальный фильтр насыщенности:



Он работает как бы в обе стороны и в обесцвечивание (можно дойти до полностью черно-белого изображения), и в насыщение. Все зависит от соответствующего коэффициента.

Вообще играться с фильтрами можно долго, получая самые разные результаты:



* Использованные в этом примере матрицы можно посмотреть на GitHub, если они вдруг вам понадобились. Для вставки в статью их объем будет избыточным.

Но давайте все же уделим немного внимания тому, где это собственно применить. Понятно, что сама идея замены цвета для каждого пикселя наводит на мысли о шейдерах для обработки фото, либо для постобработки какой-то 3D-сцены, но может быть это еще где-то есть во фронтенде?

Фильтры в CSS

В CSS у нас есть свойство filter. И там, в частности, есть вот такие варианты фильтров, связанных с цветами:

• brightness (мы его сделали)
• contrast (сделали)
• invert (то же, что и контраст, только коэффициенты по главной диагонали с другим знаком)
• saturate (сделали)
• grayscale (как уже отметили, это частный случай saturate)
• sepia (очень размытое понятие, разные варианты сепии получаются игрой с коэффициентами, где мы так или иначе уменьшаем присутствие синего цвета)

И эти фильтры принимают на вход коэфициенты, которые потом в том или ином виде подставляются в те матрицы, которые мы сделали ранее. Теперь мы знаем, как эта магия устроена изнутри. И теперь понятно, как эти фильтры комбинируются в недрах интерпретатора CSS, ведь здесь все строится по тому же принципу, что и с координатами: умножаем матрицы складываем эффекты. Правда пользовательской функции matrix в этом свойстве в CSS не предусмотрено. Но зато она есть в SVG!

Фильтры-матрицы в SVG

В рамках SVG у нас есть такая штука, как feColorMatrix, которая применяется при создании фильтров для изображений. И здесь у нас уже есть полная свобода можем сделать матрицу на свой вкус. Синтаксис там примерно такой:

<filter id=my-color-filter>    <feColorMatrix in=SourceGraphics        type=matrix,        matrix=1 0 0 0 0                0 1 0 0 0                0 0 1 0 0                0 0 0 1 0                0 0 0 0 1    /></filter>

А еще SVG фильтры можно применить к обычным DOM-элементам в рамках CSS, там для этого есть специальная функция url Но я вам этого не говорил!

На самом деле SVG-фильтры в рамках CSS до сих пор не поддерживаются всеми браузерами (не показываю пальцем на IE), но ходят слухи, что Edge окончательно переезжает на хромиумный движок, и старые версии лишатся поддержки в обозримом будущем, так что пора эту технологию осваивать, с ней можно много всякого интересного делать.

А что еще бывает?

Помимо эффектов для картинок, построенных по принципу трансформаций, есть разные штуки построенные на смещениях пикселей, смешениях их цветов и других манипуляциях, где матрица может быть удачным форматом хранения данных, по которым эта самая манипуляция должна происходить.

Kernel matrix

В частности во фронтенде мы встречаем такую штуку, как kernel matrix, и связанными с ней эффектами. Суть проста есть квадратная матрица, обычно 3x3 или 5x5, хотя может быть и больше, а в ней хранятся коэффициенты. В центре матрицы для текущего пикселя, вокруг центра для соседних пикселей. Если матрица 5x5 то появляется еще один слой вокруг центра для пикселей, находящихся через один от текущего. Если 7x7 то еще один слой и.т.д. Иными словами мы рассматриваем матрицу как такое двумерное поле, на котором можно расставить коэффициенты по своему усмотрению, уже без привязки к каким-то уравнениям. А трактоваться они будут следующим образом:

для каждого пикселя картинки {    новый цвет пикселя =        сумма цветов соседних пикселей, умноженных на их коэффициенты из матрицы}

Чистый канвас не очень подходит для таких задач, а вот шейдеры очень даже. Но нетрудно догадаться, что чем больше матрица, тем больше соседних пикселей мы будем использовать. Если матрица 3x3 мы будем складывать 9 цветов, если 5x5 25, если 7x7 49 и.т.д. Больше операций больше нагрузка на процессор или видеокарту. Это неизбежно повлияет на производительность страницы в целом.

По возможности используйте маленькие матрицы для подобных эффектов, если вам нужно их накладывать куда-то в реальном времени.

В рамках SVG у нас есть специальный тег feConvolveMatrix, который сделан как раз для создания подобных эффектов:

<filter id=my-image-filter>    <feConvolveMatrix        kernelMatrix=0 0 0                      0 1 0                      0 0 0    /></filter>

Здесь мы сделали простейший фильтр для картинки, который не делает ничего новый цвет для каждого пикселя будет равен текущему, умноженному на 1, а значения для цветов соседних пикселей умножатся на 0.

Обратите внимание, что разные браузеры рендерят SVG по-разному, и цветопередача тоже может плавать в очень широких пределах. Порой разница просто катастрофическая. Так что всегда тестируйте свои SVG фильтры или используйте canvas это более предсказуемая штука в нашем контексте.

Если мы начнем расставлять числа по слоям, от большего у меньшему, то получится blur:



Чем больше матрица, чем больше соседних пикселей мы затрагиваем, тем сильнее мылится картинка. Главное здесь не забывать нормализовать значения, а то изображение просто засветится.

Теперь, зная как работает blur, мы можем понять, почему активное его использование на странице в рамках CSS или SVG ведет к тормозам для каждого пикселя браузер проделывает кучу расчетов.

Если начать экспериментировать со сменой знаков у коэффициентов и расставлять их в разные паттерны, то получатся эффекты sharpen, edge detection и некоторые другие. Попробуйте поиграть с ними самостоятельно. Это может быть полезно.



Таким образом можно делать разные эффекты для фотографий, или даже видео, в реальном времени, и делать их зависящими от каких-то действия пользователя. Здесь уже все зависит от вашей фантазии.

Промежуточные итоги

Обобщим сказанное в этой части:

• Матрицы могут использоваться не только для трансформаций, связанных с координатами, но и для создания цветовых фильтров. Делается все по тому же принципу.
• Матрицы могут использоваться как удобное 2D-хранилище для каких-то данных, в том числе разных коэффициентов для визуальных эффектов.

Заключение

Если немного абстрагироваться от запутанных алгоритмов, то матрицы станут вполне доступным инструментом для решения практических задач. С их помощью можно своими руками рассчитывать геометрические трансформации, в том числе в рамках CSS и SVG, строить 3D сцены, а также делать всевозможные фильтры для фотографий или для постобработки изображений в рамках WebGL. Все эти темы обычно выходят за рамки классического фронтенда и больше связаны с компьютерной графикой в целом, но, даже если вы не будете решать эти задачи непосредственно, знание принципов их решения позволит лучше понимать, как устроены некоторые ваши инструменты. Это лишним никогда не будет.

Надеюсь, что эта статья помогла вам разобраться в теме практического применения матриц во фронтенде, ну или по крайней мере дала основу, от которой можно оттолкнуться при своем дальнейшем развитии. Если вы считаете, что какие-то еще темы, связанные с математикой или физикой, достойны такого же обзора в контексте верстки, то пишите свои мысли в комментариях, возможно в одной из следующих статей речь пойдет и о них.

Привет, Хабр.

В этом году я обнаружила, что не усвоила даже школьный курс математики. Я хочу наверстать упущенное, даже завела канал Math's Not Dead в телеграме. Там я буду делиться интересными, полезными и вдохновляющими штуками про математику, которые найду.

Впервые попробовала в себя в роли оператора и видеомонтажера, ниже расшифровка подкаста про математику с MagisterLudi и Алексеем Савватеевым.



MagisterLudi: Савватеева знаю с 2016 года, пару раз в год пересекались в детских программистских лагерях. Вот у меня накопились вопросы к этому удивительному человеку. Это мой первый подкаст в жизни, а еще за день до этого я всверлил себе три импланта, поэтому я немного помятый.

Что для вас математика и как вы ее определяете?

MagisterLudi: Немного контекста, я был в школьном лагере и очень расстроил одну девочку, когда доказал ей, что математика не наука.

Савватеев: Ты исходил из определения научного подхода. Ты дал некоторое определение, после чего доказал, что в соответствии с ним что-то верно. Ровно так поступил Вассерман в своем знаменитом ролике. Он дал свое определение Бога и доказал, что Бог в соответсвии с его определением отсутствует.



И важно не то, что Вассерман дал неправильное определение Бога, а что определения Бога не существует. Это не подлежит научному изысканию. И это то, что никак не могут понять саентисты. Существуют области знания вне науки, т.е. я знаю, но пришел к этому не научным путем.

К сожалению некоторые люди в точности, как саентисты, только наоборот, пытаются научно доказать, что Бог есть, что тоже абсурдно и несколько дискредитирует религиозное знание.

Знание бывает разных видов. Для гуманитарных наук то определение науки, которые ты дал, не подходит.

Я бы очень сильно расширил понятие наука. Наука это знание, в котором возможен диссертационный совет. В котором 30-40 уважаемых в данной области людей, искренних, честных и бескорыстных, собрались и могут решить, что одно глубокое научное исследование, а другое дешевка.

Если есть есть возможность созвать такой совет в какой-то области знания, то эту область знания я назову научной. Туда попадает и богословие, и история, и точные науки, куда же без них.

Как только есть область, в которой мы можем констатировать, что такие оценки возможны, а область эта долго живет, не скатываясь в коррупцию, то в этом месте есть научное знание.

А если возникает две и более группировок? Насколько я знаю, в математике такое было несколько раз.

Савватеев: В математике это было даже реже, чем в других науках. Это нормально. Научный поиск допускает, что долгие периоды могут существовать разные школы восприятия чего-то совершенно противоположным образом. Вплоть до того, что эти школы считают друг друга шарлатанами. Но если в обеих группировка сидят искренние, бескорыстные люди, то значит это просто стадия разобщения в данной области знания, которая скорее всего будет преодолена.

К примеру, за 50 лет выяснится, что одна из группировок скатилась в шарлатанство, и тогда вторая победила, как взгляд на мир. При чем даже не обязательно, что это умышленное шарлатанство. Просто область обмелела, из нее ушло что-то. А в другом месте наоборот возникает энтузиазм и рост. Вот это что-что, прошу прощения, я называю святой дух.

Он покидает какие-то области знания, переходит в другие места. Это всегда видно по оживленным конференциям, по беседам. Мне очень интересно бывать в таких местах. Не очень важно, что я не разбираюсь в данной области.

Сейчас такие места это конференции программистов. Я программирование вообще не знаю. Но я вижу, как там сейчас все активно, это хорошо чувствует мой старший сын, который пошел в эту сторону.

Там энтузиазм из всего прет. Объявляют как-то открытый чемпионат среди школьников по программированию. 145 команд школьников 8-10 классов без учителей в свой единственный выходной день сидят что-то кодят. Сразу понятно, что здесь горит огонь.

В этих местах мне интересно бывать, интересно говорить с людьми, к этому причастными.

А в математике огонь горит?

Савватеев: Конечно, ты зайди в Стекловку.



Математический институт им. В. А. Стеклова Российской академии наук

Рома Михайлов рассказывал, что он шел по коридору Стекловки в черном балахоне с капюшоном, открывал подряд двери аудиторий и говорил: Ниндзя искусство ждущих. Реакция была от страха до игнора, но один молодой сотрудник встал и со страшным интересом начал вести с ним беседу, узнавать что такое ниндзя, в каком смысле это искусство ждущих. Сейчас это гениальнейший молодой российский математик. Рома сказал, что еще тогда понял, что он станет хорошим математиком, потому что настоящий математик должен быть любопытным.



Жизнь в математике горит огнем. Математика удивительная область, в которой этот огонь не иссякал. Может быть в средние века были казусы, за них я не отвечу, но последние 500 лет такого не было ни разу.

Когда пошел Кардано, когдаБомбелли придумал комплексные число, это почти 500 лет назад, с тех пор математика не иссякала.

Время от времени возникали какие-то казусы. Например, ван дер Варден взял на себя управление кафедрой алгебры во время оккупации. На нем еще долго висел ярлык коллаборациониста, сотрудничавшего с фашистами. Хотя человек просто хотел заниматься математикой, больше ничем.

Время от времени математикам попадало от мира, но это не меняет картины, что математика как параллельная вселенная, которая постоянно развивалась.

Мы до 19 века знали про физику одно. Было совершено очевидно всем, что динамическая система, т.е. система дифференциальных уравнений, она и в одну и в другую сторону предсказывается на любой горизонт. Соотвественно не бывает необратимости по времени, любой процесс ты можешь отправить во времени в нужную сторону, и этот процесс потечет в соотвествии с системой дифуров. Все же описано этой системой, даже атомы. Приходит Больцман и говорит, что возникает на следующем уровне понимания необратимость, второй закон термодинамики. Его затравливают, он застреливается.

В математике были трагедии, но они не были связаны с тем, что человек говорил что-то неправильно в науке, с точки зрения других. Я не знаю таких историй.

Шамура самоубился со своей будущей женой, хотя причины там были совершенно не ясны, с математикой у него все было хорошо. Тьюринга затравили за то, что он был гомосек, но это уже серьёзные перегибы на местах. Трагедии были, но чтобы из-за переворотов научного движения не было никогда.

Были знаковые результаты. Стояла континуум-гипотеза, тут приходит Коэн и горит, что вы ее не докажете и не опровергните.



Казалось бы, вот у меня рациональные числа, а вот все вещественные. Как может быть, что мне достаточно понимать, как устроено то и другое, чтобы установить, есть ли между ними какое-то множество. Вопрос в чем, можно ли указать такое множество, между рациональными и вещественными, что оно не равномощно рациональным и не равномощно вещественным. Оказывается, что на этот вопрос нельзя ответить.

Таких явлений было несколько, но они наше понимание математики сильно углубляли.



Про доказательство. Есть книга Изменчивая природа математического доказательства. Как я понимаю, это скользкая тема. Что такое доказательство? Как это развивалось? Стивен Вольфрам, вон вообще написал "New kind of science".

Савватеев: Проблема Виноградова была окончательно решена в 2013 году несколькими иностранцами. Проблема Виноградова: любое нечетное число либо простое, либо сумма трех простых. Она близка к нерешенной проблеме Гольдбаха (любое четное число является суммой двух простых). Из проблемы Гольдбаха сразу следует и теорема Виноградова, но обратное не верно. Теорема Виноградова более слабое утверждение.

Виноградов доказал в 1937 году это для всех достаточно больших чисел при помощи хитрых тригонометрических сумм, в которых я еще не разобрался. Граница, до которой нужно проверять, раньше была очень высоко. В 2013 году ее опустили до 10 в 30-ой степени, потом включили компьютер и до 10 в 30-ой все перебрали. На сегодня эта теорема установленный факт.Не будешь же ты сам это все считать? Ты задаешь компьютеру правила игры.

Я нормально к этому отношусь. Если ты видишь код, в котором нет ошибок, то все хорошо. Если речь о том, что мы более часто будем применять такой способ окончания доказательства, то почему бы и нет.

В любом случае, алгоритмические проблемы меня не очень трогают. Я вижу, что в них жизнь есть, но меня они интересуют с точки зрения собранию людей, которые этими проблемами занимаются. Я всегда с удовольствием для них выступлю, побеседую с ними, но проблематика мне не близка. Почему так интересная проблема разрезания торта мне не понятно. Хотя я сам в 2016 году рассказывал, что решена проблема разрезания торта на n частей без зависти. Круто, но я не могу увидеть себя решающим себя какой-то вид этой задачи. Другое дело диофантово уравнение! Но это уже дело вкуса.

Что еще лично вам интересно?

Савватеев: Сейчас я взял на Stepik курс Никиты Калинина по гомологиям. Я в серьез решил занятая этой темой.

И как учатся математики?

Савватеев: Очень трудно. Я смотрю видео. На мехмате я что-то похожее видел, но это было очень давно. На шапочном уровне я понимаю, что такое гомология тора. Но это остаточная память. Я хочу разобраться нормально, чтобы считать.

Мне очень трудно. У меня мало времени, я урывками, в самолетах, поездах смотрю. После того, как посмотрел видео, предлагается несколько задач. Я вчера ехал на поезде 1,5 часа и за это время решил одну задачу. Формально вывести гомологию любого дерева, ну, формально вывел. Нормальный человек, который знает гомологии, или знает ответ на зубок, или выведет за 3 минуты.

Постигая науку,ты сильно сокращаешь время обдумывания типовых задач. Это и есть изучение новой науки.

Мне сейчас это очень интересно. Думаю после этого курса я буду гораздо лучше понимать высокую математику, а это и есть моя жизненная цель. Догнать этот поезд. Даже не самому вскочить и что-то открывать, а понять, как доказали теорему Ферма, что за методы использовали. В идеале, может даже гипотезу Пуанкаре, но это еще сложнее. Я хочу чтобы для меня наполнились смыслом все эти страшные закорюки в алгебраических книгах и статьях. Это глобальная цель, на пенсии я возьмусь за это всерьез. А пока занимаюсь просвещение человечества.

Какая сейчас структура у математики в мире?

Савватеев: Москва самый концентрированный в плане математики город мире. А Стекловка здание с самой высокой концентрацией работающих математикой на квадратный метр.

В Москве давняя традиция, и это самая большая и самая жирная точка на карте. В России всего две жирных точки Москва и Питер. И маленькая в Новосибирске. Ну и несколько исчезающих, где 1-2 специалиста город и они через интернет поддерживают свой уровень.

Наверно, похожая ситуация во Франции, там основная концентрация в Париже, и может несколько маленьких точек по интересам, как я понимаю. Про Японию я уже не уверен. В Америке есть много мелких точек.

Вообще где есть математика: Россия, Франция, Япония, Америка, плюс Китай появляется на карте. Там в некоторых университетах заданы безумные правила игры, с гигантскими гонорарами для приезжающих западных профессоров, плюс в Китае не нужно поддерживать гендерно-рассовый баланс. И это многих подкупает. Думаю, из-за этого в будущем Китай займет очень серьезные позиции. Корея тоже будет занимать серьезные позиции. У нас есть прекрасный шанс, но мы его бездарно теряем.

У нас есть шанс собрать всех. Точнее при правильно политике завтра здесь будут все.

Как?

Савватеев: Мы могли бы пригласить на очень хорошие зарплаты и полную свободу самовыражения иностранных и наших уехавших профессоров. Давать визы всем ученым без приглашений и волокиты. Приезжает известный математик в российский аэропорт, ему тут же выдают визу на неограниченный срок. Пусть работает в Стекловке сколько хочет, никаких ограничений, никаких пропусков, никакого надзора.

Сейчас проблема в том, чтобы приехать в Россию?

Савватеев: Да, для иностранца нереально сложно получить визу. Может Петер Шольце и хотел бы поработать в Стекловке, у него здесь много друзей. Но это нереально, нужно писать бесконечные приглашения, заверять во всевозможных отделах. Жуть.



Петер Шольце

Ваша первая кандидатская была по коррупции. Как прикладная математика может быть конкурентным преимуществом?

Савватеев: В общем, 55 основных сюжетов теории игр, и ты царь. У меня даже есть курс 57 сюжетов теории игр. Его достаточно, чтобы потом смотреть на конфликт в каком-нибудь совете директором и понимать его суть, куда надо давить и что произойдет дальше.



Теория игр это база. А что дальше?

Савватеев: Дальше надо понимать, как устроены криптовалюты. Думаю, в мире есть человек 10, которые претендуют на полное понимание происходящего. А именно 3 области знают в совершенстве: теорию игр, конечную арифметику (эллиптические кривые, конечные поля и пр) и программирование.

Первое и второе пожалуйста, третьего у меня нет вообще, так что я в эти 10 человек не вхожу. Но две области из трех знают тысячи людей, и я один из них. Теоретико-игровую подоплеку биткоина я хорошо понимаю, математическую тоже, программистскую никак. Человек, который во всех трех областях ориентируется, получает ключи ко всему.

Кто такой Сатоси Накамота? Какие теории ходят в математических кругах?

Савватеев: Я его назову. Есть серьезные подозрения, что этот Джон Нэш. По когтям видно льва. Нэш безусловно обладает всеми требуемыми свойствами. Непонятно, кто еще мог такое сделать. Кроме того, у него есть статья идеальные деньги. Было ясно, что он в этом направлении думает.



Я бы 10% поставил на то, что это лично Джон Нэш и сделал. 10% потому, что там настолько все расплывчато, что дать больше 10% конкретному имени нельзя. Это конечно одно лицо. Это не может сделать много человек. Это такая концентрация мысли, которая в коллективе недостижима. Это должно быть под одной крышей.

Один человек или коллектив? Кто сейчас двигает науку?

Савватеев: Сложно сказать. Я бы сказал, что есть понятие математический фундамент, которое вполне доступно одному человеку. Людей, которое его знают, на планете несколько сотен.

Конечно, знать все результаты, локальные результаты дифгеометрии, прочитать все тома по теории особенности невозможно.

Неправильно сказать, что наука разрослась до развала на листочки. Правильнее сказать, что дерево сохраняется, оно огромное, все ветки не знает никто, но корень знают многие. Математик математику безусловно объяснит минут за 5 чем он занимается и из какой это области.

А двигают ли науку отдельные математики, такие как Гротендик или Колмагоров, вот тут я не уверен, что есть такие. Сейчас наверно речь об отдельных гениях, который закрывают отдельные проблемы, как Перельман. И о цветнике из 100 ярчайших математиков, которые знают о результатах друг друга, быстро эти результаты узнают и аккуратно двигают эту машину вперед.

Я бы не сказал, что все совсем плохо, но могло бы быть гораздо лучше. Мы могли бы быть не одной из стран, где математика развивается, а одной единственной. Но в целом математика хорошо себя чувствует, лучше многих других областей знаний.

Как пополнять ряды?

Савватеев: Это штучное дело.

Если речь о том, чтобы население было мало-мальски грамотное, это одна задача, а если про пополнение рядов, то это другая задача и она решается. И у нас и в некоторых других странах тоже.

У нас это лучшие матшколы. Если ты попал в матшколу, то тебя за шиворот туда притащат. Ну, ладно, есть люди, которые бросают матшколы. Но в целом, пополнять ряды нужно через лучшие математические школы.

Если у меня человек рассказывает, что сын выигрывает районные олимпиады, а дальше дело не идет, я сразу спрашиваю в какой школе учится ребенок. В обычной дворовой. И еще хуже: в английской частной. Этого не нужно. Надо пойти в матшколу. Там половина всех уроков будет математика. Он будет в движухе, в этих олимпиадах с утра до ночи.

Я сам люблю гуманитарные науки, но все же у меня есть фашистское высказывание: Заниматься историей на уроке математики это преступление, а заниматься математикой на уроке истории героизм. Так я учился в физтех лицее, но прошу не передавать это своим учителям, а считать это шуткой.

Суть в том, что в лучших матшколах этим героизмом занимаются все время. Все есть математика. Математика плюс спорт.

У меня сын занимается двумя видами деятельности: он либо играет в футбол, либо решает задачи, готовится к олимпиаде, что-то прогает.

Это единственный входной билет. Во-первых, надо родится достаточно способным, тут уже ничего не сделаешь. Во-вторых, услышать этот зов в себе. И тогда ты идешь в матшколу, попадаешь в коллектив, и автоматом пополняешь ряды.

Допустим, живет парень во Владивостоке, учится в физмат-школе. А что дальше? Какие сейчас механизмы есть?

Савватеев: Я не знаю про Владивосток, есть ли там школы уровня нашей 179. Есть школы, в которых так же как в Москве научат. Более-менее. Это набор городов 40-50. И если ты попал в город, где такая школа есть, то однозначно надо идти в нее. Никакого другого варианта нет.

Хуже, когда ты попал в город, в котором нет математического образования, такие места в России есть. Тогда два варианта. Либо ты находишь бесконечную мотивацию и сидишь все время в Zoom на вебинарах. Либо ты едешь в СУНЦ. То есть переезжаешь в город, в котором такая школа есть. В 239 школу в Питере поступаешь, к примеру.



Специализированный учебно-научный центр МГУ

Ты не можешь учиться в обычной школе и думать, что на физтехе ты получишь не 2. Получишь 2. Точно.

Если грамотный учитель математики в городе есть к нему.

Есть карта таких грамотных учителей?

Савватеев: Пытались создавать, но там все непостоянно. В Омске стояла точка, а потом этого препода сманили.

Есть существенная проблема, Москва высасывает оставшихся учителей к себе. Помимо обнищания московского учительского корпуса, начинается высасывание из России всех остатков. Социально-культурный уровень в провинции, если он 20 лет назад был ниже, чем в столице, то сейчас он катастрофически ниже, чем в Москве.

Я это знаю не понаслышке, я изъездил всю страну, и не был еще только в 6 регионах из 85.

У нас в стране каждый год 1000 новых гениальных школьников оканчивают школу. Это ты не убьешь. Но они могут уехать в Китай.

У меня есть три пункта спасения нашего образования.

Первый пункт. Распустить Роспотребназор.

Второй пункт. В 3-4 раза поднять зарплаты обычным учителям.

Сегодня из 1 500 000 требуемых учителей, есть только 1 100 000. 400 000 позиций не заняты. Факт в том, что если заходишь в сельскую Адыгею, то там физрук ведет математику. Учителя математики не существует. А по физике тем более.

Ты заходишь в Следянку, а там куратор из Иркутска включает лекции Павла Виктора, великиго физика из Одессы. И понятно, что ребята не слушают ничего, это бесполезно, они не будут слушать то, что на экране.

Идея Минестерства образования о том, что учитель больше не нужен, она пагубна и просто преступна. Первое, что я изменил бы, это идея о том, что учитель уважаемая профессия, это служение. За слово услуга бить по губам.

Недавно об этом хорошо написал некто Александр Давыдов на Народном соборе. Вообще народный собор довольно истерическое издание, но время от времени там попадаются интересные статьи. Статья Давыдова одна их них. Там все разложено по полочкам. Что с образованием надо делать, как к нему относиться и что происходит сегодня.

Если я министр просвещения, я буду делать все, чтобы выборы из школ убрать.

Третий пункт.

Это возвращение наших соотечественников и по договоренности с МИДом великих иностранных ученых без виз. Надо опубликовать в интернете список лиц, который в любой момент без документов могут приезжать и жить в России.

Я знаю больше количество иностранцев, которые обожают Россию, очень хотят сюда попасться но визу получить не могут. Российская виза это полная жопа. Хуже, говорят, только американская.

Около 10 000 человек могут приехать. При чем, чтобы если человек приезжает, он сразу получает высокую зарплату. Просто так, за то, что он работает в России. Без контроля.

Да, возможно 100 из этих 10 000 сопьются. Я думаю, что не больше. В плане сопьется без продолжения работы. Ну еще 1000 сопьется прекрасно продолжая работу. Но ничего страшного в этом нет, это не препятствие.

Это гарантированный взлет. Если все это сделать, на следующий день мир нашу страну не узнает.

Если я пойду в политику, у меня будет один лозунг: Россия будет образованной. Про свободной не обещаю.

Спасибо большое! До следующих эфиров.

===============================

Алексей Савватеев ведет канал на ютубе, где выкладывает разной сложности лекции по математике.

===============================
Math's Not Dead телеграм-канал гуманитария, который узнал, что математика может быть понятной и увлекательной.

Понимаем и создаём

Хорошие новости перед статьей: высоких математических скиллов для прочтения и (надеюсь!) понимания не требуется.

Дисклеймер: кодовая часть данной статьи, как и предыдущей, является адаптированным, дополненным и протестированным переводом. Я благодарна автору, потому что это один из первых моих опытов в коде, после которого меня поперло ещё больше. Надеюсь, что на вас моя адаптация подействует так же!

Итак, поехали!

Структура такая:

Что такое цепь Маркова?
Пример работы цепочки
Матрица переходов
Модель, основанная на Марковской цепи при помощи Пайтона генерация текста на основе данных

Что такое цепь Маркова?

Цепь Маркова инструмент из теории случайных процессов, состоящий из последовательности n количества состояний. Связи между узлами (значениями) цепочки при этом создаются, только если состояния стоят строго рядом друг с другом.

Держа в голове жирношрифтовое слово только, выведем свойство цепи Маркова:

Вероятность наступления некоторого нового состояния в цепочке зависит только от настоящего состояния и математически не учитывает опыт прошлых состояний => Марковская цепь это цепь без памяти.

Иначе говоря, новое значение всегда пляшет от того, которое его непосредственно держит за ручку.

Пример работы цепочки

Как и автор статьи, из которой позаимствована кодовая реализация, возьмем рандомную последовательность слов.

Старт искусственная шуба искусственная еда искусственная паста искусственная шуба искусственная конец

Представим, что на самом деле это великолепный стих и нашей задачей является скопировать стиль автора. (Но делать так, конечно, неэтично)

Как решать?

Первое явное, что хочется сделать посчитать частотность слов (если бы мы делали это с живым текстом, для начала стоило бы провести нормализацию привести каждое слово к лемме (словарной форме)).

Старт == 1
Искусственная == 5
Шуба == 2
Паста == 1
Еда == 1
Конец == 1

Держа в голове, что у нас цепочка Маркова, мы можем построить распределение новых слов в зависимости от предыдущих графически:



Словесно:
состояние шубы, еды и пасты 100% за собой влекут состояние искусственная p = 1
состояние искусственная равновероятно может привести к 4 состояниям, и вероятность прийти к состоянию искусственной шубы выше, чем к трём остальным
состояние конца никуда не ведет
состояние старт 100% влечет состояние искусственная

Выглядит прикольно и логично, но на этом визуальная красота не заканчивается! Мы также можем построить матрицу переходов, и на её основе аппелировать следующей математической справедливостью:



Что на русском означает сумма ряда вероятностей для некоторого события k, зависимого от i == сумме всех значений вероятностей события k в зависимости от наступления состояния i, где событие k == m+1, а событие i == m (то есть событие k всегда на единицу отличается от i).

Но для начала поймем, что такое матрица.

Матрица переходов

При работе с цепями Маркова мы имеем дело со стохастический матрицей переходов совокупностью векторов, внутри которых значения отражают значения вероятностей между градациями.

Да, да, звучит так, как звучит.

Но выглядит не так страшно:


P это обозначение матрицы. Значения на пересечении столбцов и строк здесь отражают вероятности переходов между состояниями.

Для нашего примера это будет выглядеть как-то так:


Заметьте, что сумма значений в строке == 1. Это говорит о том, что мы правильно всё построили, ведь сумма значений в строке стохастический матрицы должна равняться единице.

Голый пример без искусственных шуб и паст:


Ещё более голый пример единичная матрица для:
случая когда нельзя из А перейти обратно В, а из В обратно в А[1]
случая, когда переход из А в В обратно возможен[2]


Респекто. С теорией закончили.
Используем Пайтон.

Модель, основанная на Марковской цепи при помощи Пайтона генерация текста на основе данных


Шаг 1.
Импортируем релевантный пакет для работы и достаём данные.

import numpy as npdata = open('/Users/sad__sabrina/Desktop/док1.txt', encoding='utf8').read()print(data)В теории вероятностей и смежных областях, марковский процесс , названный в честь русского математика Андрея Маркова , является случайным процессом , который удовлетворяет свойство Маркова (иногда характеризуются как  memorylessness ). Грубо говоря, процесс удовлетворяет свойству Маркова , если можно делать прогнозы на будущее процесса , основанного исключительно на его нынешнем состоянии точно так же , как можно было бы знать всю историю процесса, а значит , независимо от такой истории; т.е., условно на нынешнее состояние системы, ее прошлое и будущее государства независимы .

Не заостряйте внимание на структуре текста, но обратите внимание на кодировку utf8. Это важно для прочтения данных.

Шаг 2.
Разделим данные на слова.

ind_words = data.split()print(ind_words)['\ufeffВ', 'теории', 'вероятностей', 'и', 'смежных', 'областях,', 'марковский', 'процесс', ',', 'названный', 'в', 'честь', 'русского', 'математика', 'Андрея', 'Маркова', ',', 'является', 'случайным', 'процессом', ',', 'который', 'удовлетворяет', 'свойство', 'Маркова', '(иногда', 'характеризуются', 'как', '', 'memorylessness', ').', 'Грубо', 'говоря,', 'процесс', 'удовлетворяет', 'свойству', 'Маркова', ',', 'если', 'можно', 'делать', 'прогнозы', 'на', 'будущее', 'процесса', ',', 'основанного', 'исключительно', 'на', 'его', 'нынешнем', 'состоянии', 'точно', 'так', 'же', ',', 'как', 'можно', 'было', 'бы', 'знать', 'всю', 'историю', 'процесса,', 'а', 'значит', ',', 'независимо', 'от', 'такой', 'истории;', 'т.е.,', 'условно', 'на', 'нынешнее', 'состояние', 'системы,', 'ее', 'прошлое', 'и', 'будущее', 'государства', 'независимы', '.']

Шаг 3.
Создадим функцию для связки пар слов.

def make_pairs(ind_words):    for i in range(len(ind_words) - 1):        yield (ind_words[i], ind_words[i + 1])pair = make_pairs(ind_words)

Главный нюанс функции в применении оператора yield(). Он помогает нам удовлетворить критерию цепочки Маркова критерию хранения без памяти. Благодаря yield, наша функция будет создавать новые пары в процессе итераций(повторений), а не хранить все.

Тут может возникнуть непонимание, ведь одно слово может переходить в разные. Это мы решим, создав словарь для нашей функции.

Шаг 4.

word_dict = {}for word_1, word_2 in pair:    if word_1 in word_dict.keys():        word_dict[word_1].append(word_2)    else:        word_dict[word_1] = [word_2]

Здесь:
если у нас в словаре уже есть запись о первом слове в паре, функция добавляет следующее потенциальное значение в список.
иначе: создаётся новая запись.

Шаг 5.
Рандомно выберем первое слово и, чтобы слово было действительно случайным, зададим условие while при помощи строкового метода islower(), который удовлетворяет True в случае, когда в строке значения из букв нижнего регистра, допуская наличие цифр или символов.
При этом зададим количество слов 20.

first_word = np.random.choice(ind_words) while first_word.islower():    chain = [first_word]    n_words = 20    first_word = np.random.choice(ind_words)        for i in range(n_words):        chain.append(np.random.choice(word_dict[chain[-1]]))

Шаг 6.
Запустим нашу рандомную штуку!

print(' '.join(chain))независимо от такой истории; т.е., условно на нынешнее состояние системы, ее прошлое и смежных областях, марковский процесс удовлетворяет свойству Маркова (иногда

Функция join() функция для работы со строками. В скобках мы указали разделитель для значений в строке(пробел).

А текст ну, звучит по-машинному и почти логично.

P.S. Как вы могли заметить, цепи Маркова удобны в лингвистике, но их применение выходит за рамки обработки естественного языка. Здесь и здесь вы можете ознакомиться с применением цепей в других задачах.

P.P.S. Если моя практика кода вышла непонятной для вас, прилагаю исходную статью. Обязательно примените код на практике чувство, когда оно побежало и сгенерировало заряжает!

Жду ваших мнений и буду рада конструктивным замечаниям по статье!

вы нигде не найдете.

По крайней мере, у меня не получилось сделать его таковым. Требование определенного и большого числа пространственно-временных измерений (26 для более простой бозонной теории струн и 10 для более сложных суперструн) это один из наиболее неправильно понимаемых аспектов, который, собственно, является основным источником негативных чувств к данной теории. Придется очень постараться, чтобы объяснить происхождение этих странных чисел неспециалистам.

Строго говоря, действительно магическим числом является не сама D-мерность пространства-времени, а D2 измерений, поперечных струне, в которых она может колебаться (минус один для измерения времени и минус один для измерения, продольного струне). Другими словами, 1D-струна образует в пространстве-времени 2D-поверхность, называемую мировым слоем. Магическое число это число оставшихся направлений, доступных для струны. Так и выходит D-2.

Эта картинка была плохо нарисована по крайней мере тысячу раз, так что пусть будет еще одной плохой картинкой больше

24-поистине мистическое число. Джон Баэз дает фантастический отчет о том, почему его любимое число именно 24 которое является одним из драгоценных камней разбросанных по математике. Некоторые из них выглядят абсолютно ничем иным, как чистой нумерологией:

и это работает только для 24, за исключением 0 и 1, конечно. (Если вы любите сложные математические головоломки, попробуйте доказать это. А я не буду). И уж совсем невероятно, как это забавное тождество связано с неожиданно сложной и увлекательной (чудовищно вздорной) математикой и теорией струн (которая действует как клей для чудовищного вздора). Немаловажное значение имеет рождение 24/2 из ряда:

$$display$$ 1 + 2 + 3 + 4 + \ldots "=" -\frac{1}{12} $$display$$

Собственно, именно поэтому в бозонной теории струн D-2=24. В суперструнах эквивалентным безумием будет:

$$display$$ 1 - 2 + 3 - 4 + \ldots "=" \frac{1}{4} $$display$$

что дает D-2=8. В конце концов, это звучит как случайные несвязанные факты (и факты в кавычках), и хотя каждый из них может быть легко объяснен непрофессионалу, я на самом деле не объясняю, какова должна быть связь с числом измерений в теории струн. Я кажусь сумасшедшим не потому, что говорю что-то неправильное, а потому, что эти вещи непоследовательны и бессвязны. Проблема в том, что соединительная ткань слишком сложна с технической точки зрения, и с математической, и с физической, и с психологической, чтобы я мог ее просто объяснить.

Как с наименьшими возможными усилиями убедить когото, что D-2 = 24? Это намного проще, если этот кто-то принимает сумасшедшее уравнение 1+2+3+... = -1/12; но это явно не удовлетворительно строго. Даже если это можно понять, например, с помощью -регуляризации, то есть с регуляризацией теплового ядра + аналитической перенормировкой (и на этот счет уже есть много материала), то это все равно будет неудовлетворительно, поскольку нет никакой причины, по которой все эти манипуляции должны иметь какое-либо отношение к физике. Возможно ли прийти к правильным результатам без этого сумасшедшего уравнения; то есть, по сути, не сталкиваясь с какой-либо нерегулярностью для регуляризации? Да, конечно. Но как именно кратко и элементарно такое проделать?

Я обнаружил, что доказательства D=26 можно примерно классифицировать как:

1. Квантование светового конуса
   
   • с сумасшедшим уравнением. Требуется немного знаний о поляризациях массивных / безмассовых векторных бозонов.
   • без сумасшедшего уравнения. Требуется, по существу, изучить все о квантовании струн / алгебре Вирасоро.
2. Конформная теория поля
   
   • без сумасшедшего уравнения. Требуется знание конформных теорий поля и конформных аномалий.
3. Модулярная инвариантность
   
   • с сумасшедшим уравнением. Требует довольно элементарной квантовой механики и математики.
   • без сумасшедшего уравнения. Требуется элементарная КМ, но с базовым нудным комплексным анализом.

Доказательство 1.1, я недавно привел здесь. Это довольно просто, но вы должны доверять сумасшедшему уравнению. Другое доказательство с сумасшедшим уравнением 3.1, находится в слайдах Баэза.

Доказательства, свободные от безумия, любопытным образом образуют нечестивую Троицу. Каждое из них требует знания только из одной вершины треугольника, который образуют:

• Теория струн
• Теоретическая физика
• Математика

Доказательство 1.2 является наиболее распространенным во введении в теорию струн, так как вы уже изучаете необходимую физику струн в любом случае, и это математически не пугает. Доказательство 2.1 предназначено для более углубленного изучения и дает очень четкую физическую интерпретацию критического числа измерений, поскольку оно непосредственно связано с отменой конформной аномалии. Доказательство 3.2 я никогда раньше не видел оно кажется идеальным для людей, которые знают что-то из базового комплексного анализа (теорема вычетов и все такое) и некоторые азы квантовой механики, что не требует почти никаких знаний о физике струн.

Я очень старался выжать простое доказательство, которое является "строгим" (не использует сумасшедшее уравнение), но у меня ничего не вышло. Я пришел к убеждению, что три вершины треугольника следует понимать как перевод на разные языки одного и того же концептуального ядра, и это ядро нередуцируемо. Так что если два звена в цепи доведены до минимальной сложности, то третьему приходится все это съедать.

Все, что у меня вышло это следующая реализация доказательства 3.2. Оно отодвинет теоретическую и струнную физику на задний план и сосредоточит внимание на математике, то есть будет максимально строгим с математической стороны (хотя иногда будут замахи и на физику). Доказательство будет довольно длинным, но я нахожу его удовлетворительным. Мы соберем 24 по частям (как 2, умноженное на 3, умноженное на 4). Считайте это письмом с извинениями за освобождение 1+2+3+...=-1/12 в дикую природу.

Пруф

Мы уже говорили о мировой поверхности, которую струна образует в пространстве-времени. На этой поверхности мы можем установить систему координат . Очевидно, что, хотя наблюдаемые могут быть записаны в терминах этих координат, они должны быть инвариантны при изменениях координат . В конце концов, координаты изначально произвольны. Простым примером (локального) изменения координат является растяжение/масштабирование:

Итак, мы понимаем, что наблюдаемые в нашей теории должны быть инвариантны при таких масштабированиях. Это легко сделать классически, но становится очень нетривиальным, когда проблема переходит в удел квантовой механики. Эта масштабная симметрия является частью так называемой конформной симметрии мировой поверхности теории струн.

Представьте себе ситуацию, в которой струна делает петлю во времени, оставляя торовидный след в пространстве-времени. Конечно, множество возможных форм торов это все равно правильный выбор. Мы хотим вычислить вероятность того, что этот процесс произойдет с определенной формой тора, или лучше, квантовой амплитудой, квадрат модуля которой является вероятностью. Основной момент квантовой механики состоит в том, что мы можем вычислить амплитуду, суммируя по всем возможным состояниям i, каждое из которых имеет энергию , через время t. таким образом,

это общая амплитуда. Z должна удовлетворять нашим симметриям.

Важным моментом является то, что составная система AB из двух невзаимодействующих подсистем A и B имеет вид . Благодаря этому хорошему свойству мы можем сначала сосредоточиться на вычислении Z струны, колеблющейся в одном поперечном измерении, а затем возвести ее в степени D-2, чтобы заставить ее колебаться в поперечных измерениях D-2.

Подобно реальным вибрирующим струнам, струны теории струн имеют гармоники, которые являются целыми кратными фундаментальной.

Таким образом, струна почти точно похожа на настоящие гитарные струны и имеет бесконечные режимы колебаний, или гармоники, или обертоны. Каждая из них представляет собой гармонический осциллятор, который в квантовом варианте имеет энергетические уровни

Так ведь? Таким образом, Z одного квантового гармонического осциллятора будет

Геометрический ряд, который я только что суммировал, кажется, имеет отношение |r| = 1, что означает, что он на самом деле не сходится. Давайте сорвем повязку прямо сейчас: такие вот Z, определенные наивно как у нас, почти никогда не сходятся в лоренцевой (то есть пространственно-временной) теории. Часто мы, физики, говорим, что они осциллирующие, потому что мы суммируем кучу множителей exp(ix), а затем махаем руками, дескать, они каким-то волшебным образом отменяются, но это дешевая ложь мы просто имеем в виду, что они не сходятся. Это справедливо не только в теории струн, но и для всей квантовой теории поля, или для стандартной квантовой механики, или даже для низкочастотного квантового гармонического осциллятора.

И что дальше? Правильней будет сделать время комплексной переменной. Придавая ему мнимую часть, мы заставим Z сходиться. Мало того: когда вы вычисляете из этого непосредственно наблюдаемые величины, а затем возвращаете t обратно к реальной оси, вы восстанавливаете разумные ответы (которые соответствуют эксперименту, когда это возможно). Итак, это не трюк; этот рецепт наше определение того, что значит иметь квантовую теорию в пространстве-времени (не волнуйтесь, предположим, что t является сложным и в верхней полуплоскости Im t > 0.).

Чтобы вернуться в нужное русло, мы предположили, что одна струна в одном измерении имеет бесконечные моды колебаний, которые явно имеют частоты, кратные фундаментальной. На самом деле =1,2,3,... и поэтому Z для нашей 1D-струны является произведением

и со всего размаху бухаемся на дно. Безумие 1+2+3+ ... вновь настигло нас. Если бы мы были слабы духом, мы бы поддались и заменили его 1+2+3+...-1/12, и получили бы правильный ответ, пропустив почти всю математику в этой статье. Но мы здесь не для этого, мы здесь для того, чтобы выдавить 24 без использования колдовства. Поэтому давайте продолжим.

Почему расходящаяся сумма вообще появилась в этом показателе? Если вы проследите наши расчеты назад, то увидите, как оно вылазит из нулевых энергий КГО . Однако энергии нулевого уровня произвольны, и это был просто полезный традиционный выбор. В конечном счете существует двусмысленность в построении квантового ГО из классического ГО, называемая упорядочивающей двусмысленностью, поскольку вам нужно преобразовать коммутирующие переменные p, q в некоммутирующие операторы , и нет никакого предпочтительного квантования таких вещей, как pq. Нужно квантование ? Или ? Разницей будет константа произвол в энергии нулевой точки. Таким образом, наш самый консервативный заклад заключается в том, что нулевые колебания здесь фактически суммируются до конечного, но неизвестного значения:

где r неизвестное вещественное число. Обратите внимание, что безумный расчет дал бы магическое значение r = 1/24. Итак, потребуется парочка трюков:

• Я собираюсь показать, используя симметрию, что 1 / r это число поперечных измерений.
• Я собираюсь показать, используя другую симметрию, что r = 1/24 в любом случае, даже без 1+2+3+...=-1/12

Чтобы начать говорить об этих симметриях, мне нужно связать мою переменную t с формой тора. Связь заключается в том, что тор строится путем склеивания одноцветных ребер в этом параллелограмме:

где t представляется в виде точки на комплексной плоскости. (Сторону 2 выбрали чтоб частоты =1,2,3,... были целыми числами). Или для чистоты нотации примем =t/2 (+ простое масштабирование, которое, я напоминаю, является симметрией):

Заметим, что при приближении к вещественной оси тор вырождается. Это имеет физический смысл: может ли струна действительно замкнуться в себе в реальном времени? Это было бы путешествие во времени. Такое может произойти только во мнимом времени (по крайней мере, в верхней полуплоскости).

При определении , наша становится

Трюк первый

Прежде всего, если мы сдвинем +1, то получим разные параллелограммы

но они образуют один и тот же тор после склеивания (проверьте это!). Если форма на самом деле не меняется, то и физические величины не должны меняться.

Однако при этом преобразовании наша амплитуда действительно преобразуется:

Это не имеет смысла пока мы не вспомним, что это только для одного измерения. Для поперечных размеров D2 полная амплитуда равна , и она останется инвариантной, если

это уравнение определяет критическое измерение теории струн. Если мы найдем целое значение 1 / r, то теория будет иметь смысл только в D = 1/r+2 пространственно-временных измерениях.

Теперь доказать, что r = 1/24, будет не так просто. Чтож, попробуем.

Второй трюк

Другая симметрия, которую мы будем рассматривать, это -1/. Полученные торы не идентичны, но они похожи это масштабированные версии друг друга. Вы можете проверить, что исходная сторона 1 совпадает с новой стороной -1 / , а исходная сторона совпадает с новой стороной 1. Как мы уже говорили, масштабирование мирового пласта должно быть симметрией.

Таким образом, полная амплитуда должна быть инвариантной; однако мы не должны ожидать этого от . А? Разве не является полной амплитудой? Нет, я солгал, чтобы защитить вас от суровой правды. Истина (часть ее) состоит в том, что колебания на струне всегда происходят парами. Существует множество возможных характеристик этой дихотомии: левые и правые движущие силы, голоморфные и антиголоморфные, синус и косинус

Важно то, что для нашего (L теперь понимается как левый) также будет парный для сестринских колебаний. К счастью, я просто махну рукой, что так, чтобы общая амплитуда была произведением .

Однако это еще не все: хотя мы и учитывали колебания струны относительно опорного положения, нам также необходимо учитывать общее движение центра масс в пространстве. Мы хотим, чтобы струна вернулась в исходную точку через время , если мы хотим, чтобы она замкнулась в тор; но мы не можем просто хотеть этого, нам нужно включить амплитуду вероятности, чтобы это заработало.

Какова амплитуда вероятности того, что квантовая частица в 1D останется в одном и том же месте через определенное время? Намек состоит в том, что для чисто мнимых времен уравнение Шредингера является уравнением теплопроводности. И бесконечно концентрированное пятнышко тепла эволюционирует в соответствии с уравнением теплопроводности в 1D, распространяясь в гауссовский пик, пик которого уменьшается как . Таким образом, позвольте мне предположить, что амплитуда для центра масс примерно такова

Если это так, то, общая амплитуда должна быть примерно такой

и для 1/:

поэтому, если бы была трансформирована как-то так

наша общая амплитуда была бы инвариантной, и тогда теория имела бы смысл. Теперь я собираюсь доказать, что это может произойти только в том случае, если r=1/24.

Колдовство

Давайте сделаем некоторые предварительные переобозначения

Тогда, наиболее удобным вариантом представления произведения P() будет:

Я использовал разложение Тейлора для -log(1-x) и геометрический ряд. Если вы не уверены, вы можете более тщательно проверить, разумны ли эти шаги (включая своп суммы) для Im >0.

Следующий психоделический аргумент принадлежит Зигелю (да, именно Зигелю). Мы начинаем без видимой причины вот с такой функции комплексной переменной w, с в качестве параметра:

а затем, вводя еще один реальный параметр (наш завершающий ход будет заключаться в том, чтобы устремить его в бесконечность), мы строим комбинацию

Давайте посчитаем полюса g. Быстрый осмотр показывает, что существует набор простых полюсов при w=nkv и еще один при w=nktv, для k=1,2,3,...; плюс тройной полюс при w=0. Вычеты легко вычисляются следующим образом:

Если вычет в тройной точке (полюс третьего порядка) не кажется очевидным, вспомним, что разложение Тейлора котангенса в нуле начинается .

График g (w), для ( = i), ( = 1). Белые пятнышки это полюса, и порядок таков, сколько раз цвета повторяются вокруг них.

Теперь должно быть ясно, что g нам для применения теоремы вычетов. Рассмотрим траекторию бегущую против часовой стрелки вокруг параллелограмма с вершинами 1,,1,.

Теорема вычетов гласит:

Сумма на самом деле пробегает по полюсам, которые находятся внутри параллелограмма, но мы скоро увидим, что это не то, о чем нам следует беспокоиться.

Теперь я хотел бы использовать это уравнение, чтобы доказать тождество, которое нам действительно нужно. Однако я докажу это только для на мнимой оси, потому что это проще, но на самом деле это будет верно для всех Im >0. Поскольку обе части уравнения, которое я выведу, голоморфны в над верхней полуплоскостью, их согласия на прямой достаточно, чтобы доказать, что они всегда равны. Короче говоря, предположим, что пока чисто мнимое, но в конце мы можем просто отбросить это предположение.

Заделаем же интеграл на параллелограмме, который теперь ромб. Для , кажется, первообразную сходу не отгадаешь. Итак, возьмем предел . Нетрудно заметить, что f(vw) сходится к константе (1,-1,1,-1) соответственно на четырех отрезках (если вы ее не видите, запишите ее с помощью комплексных экспонент). Таким образом, в пределе интеграл равен

Легкотня! Интеграл от 1/w это log w, так что позвольте мне просто приписать его и ААА! Контур обхода! Нам нужно выбрать обход для логарифма и убедиться, что он не перепрыгивает через берег разреза. Мы можем использовать симметрию чтоб переписать

и теперь, когда весь путь находится справа, мы можем использовать отрицательную действительную ось в качестве берега разреза и, таким образом, использовать главную ветвь логарифма. Просматривая весь путь, получаем

Славненько. Теперь о вычетах. Если , то все полюса сжимаются и приближаются к началу координат; таким образом, в пределе все они находятся внутри ромба, а сумма идет по всем полюсам. Таким образом, сумма равна

на случай, если кто не помнит

и наша сумма вычетов:

Наконец-то мы возвращаемся на Землю. Это начинает выглядеть как теорема о нашем произведении P(). Теперь, когда у нас есть обе части равенства, давайте воспользуемся теоремой вычетов.

А вот и наше магическое число! По крайней мере, половина. Это все еще выглядит как тарабарщина, хотя давайте для пущей наглядности перейдем к экспонентам:

Казалось бы, ничего особенного, но комбинация

как мы недавно доказали, красиво трансформируется при преобразовании -1/:

И это все! Именно это мы и искали! Чтоб преобразовать во что надо, замечаем, что оно должно быть самим (), и поэтому r=1/24, и поэтому, наконец

Выводы

Из-за философии, лежащей в основе всего этого поста, чтобы использовать математику как можно более элементарно и чтобы она была самодостаточной, мы ускорили то, что на самом деле является невероятно увлекательной (и, конечно же, гораздо более элегантной) математикой. () это, конечно, функция Дедекинда, и мы доказали ее свойства преобразования в модулярной группе; точнее, что модулярный дискриминант является модулярной формой веса 12. Теория струн тесно связана с этой областью математики; на самом деле я надеюсь, что для тех, кто уже знает этот материал, это послужило беглым взглядом на то, что струны даже имеют отношение к модульным формам. В любом случае, я не думаю, что могу судить предмет, который я на самом деле едва знаю по-верхам, так что тут попримолкну.

Иногда всплывает интересный вопрос: если это так неправильно, то почему 1+2+3+...=-1/12, или -регуляризация / тепловое ядро / суммирование Абеля или как бы вы это ни называли, дают малой кровью тот же правильный результат, что и более строгие пути?

У меня нет ни малейшего представления, почему оно так выходит.

Инстинктивно я бы пробормотал что-нибудь о физическом резоне или аналитичности, но, честно говоря, это просто чистое безумие. Это определенно не совпадение, потому что тот же трюк работает и для суперструн. На самом деле я даже не уверен, какова точная взаимосвязь между тремя различными классами доказательств, они выглядят как совершенно разные рассуждения. В квантовании светового конуса при первом чтении вы даже не понимаете, как масштабная / конформная инвариантность вписывается она очень глубоко зарыта. И если вы случайно знаете какую-то конформную теорию поля, посмотрите, как это доказательство строит 24. Они звучат совсем не как переводы одного и того же, хотя должны.

Удивительно, как много информации о содержании теории несут доказательства D=26 (или D=10), и как много вы уже узнаете о струнах, просто пытаясь объяснить то, что по существу является самым основным фактом теории. Это наглядный пример того, что в теории струн все сходится, ничего не бросается туда просто так, все существенно.

Дополнение

Возможно, существует более быстрое доказательство, если принять теорему Эйлера о пятиугольных числах

Если вы выделите квадрат в экспоненте вы можете переписать

таким образом

С в таком виде уже реально доказать используя суммирование Пуассона.

Тем не менее, обращение к теореме Эйлера определенно похоже на мошенничество, поэтому я не пошел по этому пути.

Более 20 лет назад я заинтересовался телекомом. Я начал с чтения книжек, одной из которых был курс CCNA. Тогда это была довольно тоненькая книжечка с FDDI, Token Ring, ISDN и подобными вещами, о которых новое поколение сетевиков только слышали. И тогда я впервые прочитал про CCIE сертификацию. У меня осталось впечатление, что обладатели этого статуса являются воистину IT богами. Конечно же, мне захотелось достичь этого сетевого самадхи.

С тех пор прошло много времени. Я получил CCNA потом CCNP, с успехом просрочил все эти сертификаты за ненужностью и лет через 10 стал CCIE. Я по-прежнему занимаюсь сетями, и, надо сказать, похоже, люблю свою работу, но романтизм, конечно, прошел. Двадцать лет назад отношение ко всему этому было совсем другим. Это был драйв, это было настоящее приключение.

Сейчас такого интереса уже нет, и отношение к сертификации у разных инженеров тоже разное, да и сам я отношусь к этому неоднозначно. Я ясно осознаю, что это своеобразная игра, часто не совсем честная игра, и, если вы не знаете правил, то, даже обладая прекрасными знаниями и навыками, у вас достаточно большой шанс проиграть. В этой статье мы с помощью несложной математики рассмотрим эти правила, что позволит вам составить свою по возможности максимально честную и одновременно выигрышную стратегию.

Честный подход

Давайте попробуем понять, какой подход оценки нашего знания был бы максимально честным?

• В качестве первого условия я бы назвал ясное определение круга теоретических вопросов и практических навыков, проверяемых тестированием.
• Далее, хотелось бы, чтобы была разумная детализированность и специфичность. Какой смысл узнавать насколько хорошо я знаю несущественные в моей работе детали, и могу ли я безошибочно сделать/вспомнить/объяснить то, что пригодится мне пару раз в жизни и что легко гуглится за одну минуту. Хочется, чтобы вопросы были по существу.
• И третий, достаточно важный для данной статьи компонент это то, что я бы хотел, чтобы проверялись именно мои навыки и знание, необходимое мне в моей профессиональной деятельности, а не навыки сдавать данный тип экзамена.

Предположим, что первые два условия соблюдены. Давайте изучим зависимость честности нашего экзамена от третьего компонента.

Для определенности будем говорить именно о тестировании с бинарным результатом: сдал (получи сертификат) / не сдал (нет сертификата). Тогда результаты экзамена в одном из самых простых вариантов мы можем представить в виде следующей диаграммы:



Стрелки , , обозначают вероятности перехода из одного состояния в другое. Так, обозначает вероятность того, что вы после безуспешной попытки пытаетесь сдать экзамен еще раз. Если нет перехода между состояниями, то это значит, что вероятность перехода равна 0.

Например, вероятности могут быть распределены следующим образом



Суть тестирования данного типа в том, что тестируемые не имеют никакого инсайда, или инсайд никак не улучшает шансы пройти тест. Конечно, известны требования к практическим навыкам а также к объему и глубине теоретического знания, но нет никакой полезной информации по технике сдачи экзамена.

И именно такая ситуация на мой взгляд является идеально честной. В данном случае тестируется ваше знание, а не то, как вы научились сдавать экзамен.

Пример 1

Прекрасным примером для меня является то, как проходили устные экзамены по физике на физтехе. Это всегда очень индивидуальная беседа. Да, были билеты, но часто почти сразу переходили к задачам, вопросам, обсуждению. Все сильно зависело от преподавателя, от того, какая тема обсуждается, как вы начинали отвечать билет, а также от того, какая мысль вдруг пришла экзаменатору в голову и многих других факторов. Конечно, в данном случае сложно говорить о стандарте, и иногда сильные студенты получали меньший бал, чем слабые, но обычно все же справедливость соблюдалась.

Пример 2

В качестве другого примера можно рассмотреть технические собеседования при найме сотрудников. Если ваша компания небольшая, вы грамотно составили задание и собеседуете лишь небольшое количество людей, то, в принципе, можно составить достаточное количество вопросов-заданий, чтобы они не пересекались или построить вашу беседу интерактивно, опираясь на опыт претендентов.

Но если мы говорим про популярные сертификаты, то этот подход не работает. Причин для этого несколько, например, приведу две:

• такой индивидуальной подход слишком дорог
• нужна стандартизация

Справедливый подход

Обычно мы сталкиваемся с ситуацией, когда мы должны готовиться именно к экзамену. Я говорю не про теоретический материал и не о навыках, которыми мы должны обладать и которые безусловно важны и полезны в нашей повседневной трудовой деятельности. Я говорю о том, что мы должны вырабатывать навыки специально под данный тип экзамена (я все еще предполагаю, что дампов нет), и если вы не будете тренировать этот специфический навык, то вероятность успеха значительно снижается.

Пример

Мне кажется, что хорошим примером такого подхода является CISSP сертификация. Если вы хотите сдать этот экзамен, то обычная рекомендуется заключается в том, что вы должны сначала выучить всю теорию, а потом потратить столько же времени, отвечая на вопросы (не дампы), специально составленные для вашей тренировки. При такой подготовке в общей сложности приходится отвечать на несколько тысяч вопросов (во всяком случае, так было у меня). Таким образом, вы тренируете навык быстро понимать суть вопроса, понимать логику и смыслы, вкладываемые вендором, и просто учитесь сохранять внимательность в течении нескольких часов в условиях стресса. Таким же типом экзамена являются тесты, проводимые при приеме на работу (числовые, вербальные, логические, ...).

Вы можете натренировать этот навык заранее или путем нескольких попыток сдачи экзамена.

Этот подход по-прежнему можно считать довольно честным, потому что здесь все находятся в приблизительно в равных условиях, поэтому я назвал этот тип экзамена справедливым подходом.

Каким будет граф переходов в данном случае?



Мы имеем следующие состояния:

1. Нет опыта. Вы решили сдавать экзамен абсолютно честно, то есть, не тренируя специально технику сдачи экзамена. Вы знаете теорию и обладаете необходимыми практическими навыками. Вам кажется, что этого должно быть достаточно, чтобы получить достойную оценку.
2. Не сдал. Опыт. Это состояние, когда вы имеете дополнительное знание и навыки, касающееся процедуры проведения экзамена. Это знание было получено или в результате безуспешной попытки, или в результате целенаправленной подготовки. Еще раз напомню, что в данном случае речь не идет о дампах.
3. Сдал.
4. Сдался.

Стрелки , , , обозначают вероятности перехода из одного состояния в другое. Если нет перехода между состояниями, то это значит, что вероятность перехода равна 0.

А теперь зададимся вопросом: насколько уменьшится вероятность вашей сдачи, если вы будете ожидать честного подхода, и просто понадеетесь на ваш опыт и знания и не будете специально готовиться к технике сдачи данного экзамена (то есть нас интересует )? Конечно, если сложность экзамена такая же, как и в случае честного подхода, то ваши шансы будут такими же. Но мне кажется разумно сделать одно важное допущение, которое кардинально меняет ситуацию.

Давайте предположим, что вендор старается сохранять определенную сложность теста, и делает это, удерживая процент сдачи не выше определенного уровня. Предположим, что уровень сложности вопросов подбирается таким образом, чтобы проходной процент был бы не выше 50%.

Зададим для определенности следующие условия:

• Вендор поддерживает сложность задания на таком уровне, чтобы в среднем не более 50% претендентов успешно выполняли бы задание. Мы будем проводить расчеты на этой границе.
• Давайте предположим, что после каждой попытки 5% процентов от сдающих разочаровываются и больше никогда не пытаются пересдать экзамен (сдаются):
• Опыт увеличивает ваши шансы. Давайте предположим, что вероятность несдачи экзамена из состояния 2 на 30% меньше, чем из состояния 1:
• При этом упростим задачу и будем считать, что такое увеличение опыта происходит лишь один раз. Это предположение упростит расчет и не изменит наши выводы.
• Также будем считать, что на свой первый экзамен 50% идет с нулевым знанием об экзамене (то есть из состояния 1) и 50% специально готовятся к технике сдачи экзамена (из состояния 2). При этом мы считаем, что их реальное, полезное знание и навыки приблизительно одинаковы.

Какой процент успешной сдачи будет из состояния 1?

Теперь вероятность сдачи будет лишь 36% против 50% в случае честного подхода.
Вероятность сдачи из состояния 2 55%.

Полный же граф будет выглядеть следующим образом:




То есть, если вы пытаетесь сдавать экзамен честно, что в контексте данной статьи означает, что вы опираетесь на ваше теоретической знание и практические навыки в рамках данного экзамена, но без специфической подготовки собственно к самой процедуре экзамена, без попытки приспособить свой образ мышления к логике составителей теста, без некоторого инсайда, то вероятность того, что вы сдадите этот экзамен, уменьшается в полтора раза. Чтобы сдать таким образом, уровень вашего знания должен быть значительно выше среднего и на самом деле значительно выше того уровня, который требуется для этого экзамена.

Понятно, что при таком подходе, доля людей, пытающихся сдать честно будет уменьшаться, экзамен начинает усложняться (чтобы сохранилось условие 50%), что приводит к тому, что вероятность сдачи из состояния 1 становится все меньше и меньше.

И все-таки я считаю этот подход справедливым. Здесь нет нечестной конкуренции. Просто нужно понять, что нужно готовиться конкретно к экзамену. Без этого, даже обладая отличными знаниями, вероятность сдать тест невелика (но есть).

Теперь предположим, что есть дампы. Как изменится картина?

Дампы. Нечестная конкуренция

Теперь наша схема изменилась:



Появилось еще одно состояние Дампы. Это значит, что претендент может воспользоваться дампами экзамена, что даст ему 100% вероятность сдачи. Теперь давайте зададим конкретные условия.

• По-прежнему будем считать, что вендор поддерживает сложность задания на таком уровне, чтобы в среднем не более 50% претендентов проходили бы этот экзамен (мы оговорили это выше).
• Как и в предыдущем случае, считаем, что опыт уменьшает вероятность несдачи экзамена на 30%.
• Немного изменим вероятности перехода в состояние 4. Давайте для идеалистов ( ) увеличим этот коэффициент до 10%, для перехода оставим таким же, равным 5%. Это не сильно повлияет на результат, но это будет отражать тот факт, что шок от попытки сдать экзамен из состояния 1 будет достаточно большим (причины мы обсудим позже), и разумно предположить, что это будет чаще приводить к разочарованию.
• Предположим, что изначально всего лишь 20% претендентов используют дамп. Распределение между состояниями 1 и 2 при первой попытке будем считать равным (по 40%).
• Будем считать, что, если первая попытка (из состояния 1 или 2) оказалась неудачной, и претендент все же решил продолжать, то ровно половина из них воспользуется дампом: и

Давайте посмотрим, как изменится картина. Вот решение:



Мы видим, что вероятность сдать экзамен из состояния 1 стала всего 5%, что значит, что у вас практически нет шансов. Казалось бы, что для состояния 2 все не так уж и плохо 34%, но, в действительности, при небольших значениях такой расчет не совсем корректен. Дело в том, что наше условие опыт уменьшает вероятность несдачи экзамена на 30% искусственно ограничивает снизу вероятность тридцатью процентами (ниже быть не может), что, конечно же, не совсем правильно

Единственный вывод, который пока можно сделать это то, что при наших условиях мы можем забыть про возможность сдачи из состояния 1 (нет опыта). Очень скоро комьюнити, для которого этот экзамен представляет интерес, осознаёт это, и количество идеалистов, пытающихся сдать экзамен без соответствующей подготовки, становится пренебрежимо малым. Тогда мы получаем другую диаграмму:



При тех же условиях, что и в предыдущем примере, мы получим следующее решение:



При этом распределение на экзамене будет следующим:

Состояние 1 (опыт): %
Состояние 2 (дамп): %

Думаю, что метод доказательства очевиден из предыдущих двух примеров, поэтому я опускаю его.

Это значит, что при появлении дампов (и при тех условиях, которые мы наложили) мы получим падение вероятности сдачи для людей, которые специально готовились к экзамену или имели опыт неудачной сдачи и при этом не используют дампы с 55% до 25%, то есть более чем в 2 раза.

Теперь давайте вспомни условия.
При первой попытке у нас лишь 20% решили сразу воспользоваться дампом. После неудачной попытки лишь половина решает воспользоваться дампом. И это довольно мягкое условие привело к тому, что для претендентов, готовящихся к экзамену без дампов, сдать экзамен становится очень сложно. В среднем им придется сдавать этот экзамен 4 раза. Затраты на подготовку (время) и на сдачу становятся довольно большими. При этом можно сдать по дампу. Это потребует существенно меньшего времени на подготовку и даст практически 100% вероятность сдачи.

Итак, давайте посмотрим на плюсы и минусы, которые получает претендент в обоих случаях.

Что имеют те, кто пытаются сдавать без дампов?

• (-) потраченное время на подготовку (деньги)
• (-) потраченные деньги за неудачные попытки
• (-) в случае неудачи руководство и коллеги начинают сомневаться в их компетенции
• (+) хороший уровень знания

Те, кто сдают с дампами

• (-) стоимость дампа (необязательно: дамп может находиться в свободном доступе)
• (-) возможно, недостаточный уровень знаний (необязательно: никто вам не мешает хорошо подготовиться при этом)
• (-) морально-этические издержки, связанные с нечестной конкуренцией (необязательно и очень индивидуально)
• (+) минимально потраченные ресурсы
• (+) уважение коллег и руководства (ведь не обязательно говорить, что вы воспользовались дампом)

В принципе, теоретически все это можно выразить ценой и просто сравнить цены честной сдачи и сдачи с дампом. При этом то, что помечено минусом (-) прибавляет стоимость, а то, что положительно, наоборот, убавляет. Понятно, что некоторые вещи из списка очень индивидуальны (например, морально-этические издержки), и поэтому цена сдачи с дампом и цена честной сдачи будут сильно варьироваться для разных людей.

Когда цена дампа становится меньше цены честной сдачи, человек начинает пользоваться дампами.

Состояние насыщения

При низкой стоимости дампа это приводит к цепной реакции: чем больше людей пользуются дампами, тем сложнее становится экзамен и тем меньше вероятность сдать без дампов, что заставляет все большее количество людей прибегать к нечестной конкуренции, и в конце концов это приводит к ситуации насыщения, когда при первой попытке, количество претендентов, пользующихся дампами, уже превышает заданный проходной процент (50% в наших примерах).

В результате вендор вынужден предпринимать какие-то действия. Простейшим действием является увеличение частоты обновления тестового задания. В эти моменты дампы становятся неактуальными, и за счет этого вероятность сдачи с дампом может быть снижена.

Пример

Предположим, что экзамен меняется раз в 3 месяца, на появление нового актуального дампа уходит 2 недели, тогда вероятность сдачи с дампом падает со 100% до %. Но этого может быть недостаточно, поэтому экзамен все усложняется и усложняется, появляются разные варианты, делается так, что даже с дампом требуется интенсивная тренировка.

Таким образом,

• экзамен становится невероятно сложным
• шансов сдать без дампов мало
• даже чтобы сдать с дампами, вам приходится серьезно готовиться, фактически тренироваться
• экзамены и темы часто и неожиданно меняются. В эти моменты те, кто готовился по дампам начинают терпеть фиаско, а пытающиеся сдать экзамен честно, получают преимущество

То есть при данном подходе все же сохраняется шанс сдачи для тех, кто готовится без дампов, но уровень ваших знаний должен быть очень и очень хорошим, вы должны потратить много времени. Фактически это превращается скорее в спорт, вы должны реально тренироваться, чтобы сдать данный экзамен. И данная тренировка во многом является избыточной.

Пример

Таким экзаменом, на мой взгляд, до недавнего времени был CCIE R&S. Существуют прекрасные курсы для подготовки к CCIE, например, ine.com. Но, даже пройдя всю подготовку (что займет у вас около полугода, полностью потраченные на это), сдать экзамен все равно достаточно сложно. И параллельно с этим, во всяком случае еще несколько лет назад, вы легко могли найти бесплатные дампы в интернете, как письменных экзаменов, так и лабораторных работ.

Следствия

В действительности следствия от появления дампов с низкой стоимостью (в смысле, рассмотренном выше) являются довольно печальными. С одной стороны, мы имеем изощренно сложные тесты и лабораторные работы, которые реально очень сложно пройти. С другой стороны, полученный сертификат не гарантирует соответствующего уровня знаний.

Вы удивитесь, на какие вопросы не отвечают счастливые обладатели CCIE сертификатов. Не редко эксперты совершенно не готовы к честному собеседованию. И дело не в том, что они когда-то знали, но забыли. Дело в том, что они этого никогда и не знали. Зачем учить, тратить время, деньги, рисковать, когда можно просто зазубрить ответы на вопросы.

Конечно же, это приводит к падению авторитета экспертных сертификатов. От этого страдают не только и не столько вендоры, сколько инженеры, которые получили данные регалии честно. Происходит нивелирование того конкурентного преимущества, которое давал добытый потом и кровью статус.

Думаю, многие из вас наблюдали такую картину: сильный инженер, с хорошим практическим опытом, внимательно изучив рекомендуемую литературу, идет сдавать экзамен и проваливает его. Он обескуражен. Вопросы кажутся не относящимися к делу (и это нередко так), тексты слишком большими и запутанными, часто претендент просто не укладывается во времени. При этом его коллега, с гораздо меньшим опытом и знанием, сдает этот тест практически на 100%. Это типичный результат нечестной конкуренции.

Дампы и вендоры

Почему же вендоры не защищают авторитет своих сертификатов? Может быть это невозможно или очень дорого?

Уверен, что это возможно, и мы видим это на примере CISSP.

Для этого нужно повышать стоимость дампа. И делать это можно следующими путями:

• делать случайную выборку вопросов из гораздо большего списка, например, из 10000 вопросов
• знание, которое претендент получает при честной подготовке должно быть действительно ценным для него (что уменьшает полную стоимость честного/справедливого подхода)
• моральная-этическая составляющая цены дампа должна быть высокой. В комьюнити должно быть однозначное осуждение использования дампов
• также обычно не представляет труда найти и запретить ресурсы, распространяющие дампы

В соответствии с нашей моделью это должно вернуть тесты в русло справедливого подхода, с адекватной сложностью и глубиной проводимого тестирования.

К сожалению, из моего опыта я вижу, что вендоры часто ограничиваются только тем, что абсолютно бесплатно для них, а именно, сообщают вам, что дампами пользоваться нельзя. В принципе, это не эффективно. Если вы готовитесь к экзамену, то, конечно, вы ищите в интернете вопросы для тренировки, и, честно говоря, вы не знаете, совпадут ли какие-то вопросы с вопросами экзамена или нет.

Также хочется отметить, что дампы это не всегда что-то нелегальное, часто существуют вполне официальные курсы, на которых вам дается все тот же дамп, или разъясняются сложные моменты экзамена, но, в любом случае, это инсайд, имеющий мало общего с действительным повышением уровня знания, и, на мой взгляд, это тоже нечестная конкуренция. Если вендор хочет действительно проверить и подтвердить знание претендентов, то это должно быть запрещено.

Есть еще один хороший способ увеличить качество сертификата можно просто добавить собеседование.

Уверен, что вендоры прекрасно осознают ситуацию. Например, это легко увидеть по резкому падению процента сдающих при обновлении теста или лабораторной работы, или, например, по количеству сдавших сложный письменный экзамен с результатами близкими к 100%. То, что они ничего не делают с этим, говорит о том, что их вполне устраивает эта ситуация.

Заключение

В данной статье мы рассмотрели несколько моделей, которые я назвал

• честный подход
• справедливый подход
• нечестная конкуренция, дампы

Надо понимать, что это всего лишь модели. Например, мы считали, что существует некое требование сложности, что в реальности может быть не так или не совсем так. Но все же мой личный опыт сдачи экзаменов, опыт прохождения и проведения собеседований и общения с другими инженерами говорит о том, что, по крайней мере для некоторых сертификаций, выводы этой статьи близки к реальности.

Каждый из данных подходов накладывает определенные требования к подготовке. Честный подход требует только хорошего знания теории и хороших практических навыков. Справедливый подход требует также специфической подготовки к экзамену.

Случай нечестной конкуренции несколько сложнее, он включает в себя, например, морально-этическую составляющую, что непросто оценить. Но некоторые выводы мы все же можем сделать:

• у вас практически нет шансов сдать экзамен честно (в контексте данной статьи это значит, что вы пытаетесь пройти тест, опираясь лишь на необходимое теоретическое знание и практический опыт, без специальной подготовки именно к технике сдачи экзамена)
• нужно специально тренироваться для сдачи этого экзамена, но, чтобы сдать без дампов, ваш уровень должен быть очень высок, в действительности гораздо выше, чем разумное требование, соответствующее целям и смыслу этого экзамена
• наличие и широко практикуемая нечестная конкуренция во многом лежит на совести вендоров. На мой взгляд, именно они обязаны защищать авторитет своих сертификатов. В этих условиях, думаю, сложно осуждать инженеров, пользующихся дампами. Иногда без них цена честной сдачи становится непомерно высока, а требования к знанию многократно завышены

Казалось бы, зачем играть в эти игры? Однозначно, что это нужно не всем, но есть несколько факторов, которые важны:

• иногда сертификаты нужны для работы бизнеса (например, если вы работаете в интеграторе)
• сертификат реально увеличивает нашу вероятность найти хорошую работу
• cертификация это прекрасный способ заставить себя выучить что-то

Для меня именно последний пункт всегда являлся самым важным, а сертификаты это приятные и иногда полезные бонусы!

О законе больших чисел (збч) написано много (например, на английском, тут и тут, также [1]). В этом тексте я попробую рассказать о том, чем закон больших чисел не является об ошибочном восприятии этого закона и потенциальных ловушках, спрятанных в математических формулировках.

Начнем с того, что же такое закон больших чисел. Неформально, это математическая теорема о том, что вероятность отклонений среднего по выборке от математческого ожидания мала и что эта вероятность стремится к нулю при увеличении выборки. Совсем неформально, теорема утверждает, что с мы можем быть в достаточной степени уверены, что среднее по нашей выборке достаточно близко к настоящему среднему и таким образом хорошо его описывает. Разумеется, предполагается наличие традиционного статистического багажа наши наблюдения из выборки должны описывать одно и то же явление, они должны быть независимы, и мысль о том, что есть некоторое настоящее распределение с настоящим средним, не должна вызывать у нас существенных сомнений.

При формулировке закона мы говорим среднее по выборке, и все что может быть математически записано как такое среднее, попадает под действие закона. Например, доля событий в общей массе может быть записана как среднее, нам достаточно записать наличие события как 1 и отсутствие как 0. В итоге среднее будет равно частоте и частота должна быть близка к теоретическому среднему. Именно поэтому по ожидаем, что доля орлов при подрасывании идеальной монеты будет близка к .

Рассмотрим теперь ловушки и ошибочные представления об этом законе.

Во-первых, ЗБЧ не всегда верен. Это всего лишь математическая теорема с входными данными предположениями. Если предположения неверны, то и закон не обязан выполняться. Например, это так если наблюдения зависимы, или если нет уверенности в том, что настоящее среднее существует и конечно, или если изучаемое явление меняется во времени и мы не можем утверждать, что мы наблюдаем одну и ту же величину. По правде говоря, в определенной степени ЗБЧ верен и в этих случаях, например, для слабокоррелированных наблюдений или даже в том случае когда наблюдаемая величина меняется во времени. Однако, для корректного приложения этого к непосредственной реальности нужен хорошо тренированный специалист-математик.

Во-вторых, кажется верным, что ЗБЧ утверждает среднее по выборке близко к настоящему среднему. Однако, такое утверждаение остается не полным: надо обязательно добавлять с высокой долей вероятности; и эта вероятность всегда меньше 100%.

В-третьих, хочется сформулировать ЗБЧ как среднее по выборке сходится к настоящему среднему при неограниченном росте выборки. Однако, это неверно, потому что среднее по выборке вообще никуда не сходится, так как оно случайное и остается таковым для любого размера выборки. Например, даже если подбросить симметричную монету миллион раз, все равное есть шанс, что доля орлов будет далека от или даже равна нулю. В определенном смысле, всегда есть шанс получить что-то необычное. Надо признать, однако, что наша интуиция все-таки подсказыает нам что ЗБЧ должен описывать какую-то сходмость, и так есть на самом деле. Только сходится не среднее, а вероятность отклонения выборочного среднего от его истинного значения, и сходится к нулю. Так как эта идея интуитивно очень удобна (шансы увидеть что-то необычное стремятся к нулю), матетматики придумали для этого особый тип сходимости сходимость по вероятности.

В-четвертых, ЗБЧ не говорит ничего о том, когда выборочное среднее можно считать достаточно близким к теоретическому. Закон больших чисел только постулирует существование определенного явления, он ничего не говорит о том, когда его можно использовать. Получается, на ключевой вопрос с точки зрения практики могу ли я использовать ЗБЧ для моей выборки размера n?, закон больших чисел не отвечает. Ответы на эти вопросы дают другие теоремы, например, Центральная Предельная Теорема. Она дает представление о том, в каких пределах выборочное среднее может отклонятся от своего истинного значения.

В заключение следует отметить центральную роль ЗБЧ в статистике и теории вероятностей. История этого закона началась тогда, когда ученые заметили, что частоты некоторых повторяющихся явлений стабилизируются и перестают существенно менятся, при условии многократного повторения опыта или наблюдения. Поразительным было то, что эта стабилизация частот наблюдалась для совершенно несвязаных явления от бросания игральной кости до урожайности в сельском хозяйстве, указывая на возможное существование закона природы. Интересно, что этот закон природы оказался частью математики, а не физики, химии или биологии, как обычно бывает с законами природы.

[1] Illustrating the Law of Large Numbers (and Confidence Intervals) Jeffrey D Blume & Richard M Royall