Случайность

Случайности не случайны кто такие семейства псевдослучайных функций (PRFs)

07.12.2020 02:05:58 |

Автор: admin

В 1984 году Голдрайх, Голдвассер и Микали в своей статье формализовали концепцию псевдослучайных функций и предложили реализацию PRF, основанную на псевдослучайном генераторе (PRG) с удвоением длины. С тех пор псевдослучайные функции показали себя чрезвычайно важной абстракцией, которая нашла применение в различных сферах, например, в аутентификации сообщений и в доказательствах теорем. В этой статье я расскажу:

Что из себя представляют случайные функции (RF)
Что из себя представляют псевдослучайные функции (PRF)
Кто же такие эти ваши семейства
PRF vs. PRG
При чём тут блочные шифры

Случайность

Уже из названия становится понятно, что псевдослучайная функция это нечто выглядящее как случайная функция. Ну а что такое случайная функция в нашем случае? Для начала ограничим нашу область рассмотрения функциями отображающими строку из нулей и единиц длиной в строку из нулей и единиц такой же длины , то есть

$\underbrace{1110...0010}_{n} \rightarrow \underbrace{0100...0011}_{n} \Leftrightarrow \{0,1\}^n \rightarrow \{0,1\}^n$

Этого, вообще говоря, можно и не делать, и рассматривать отображения строк одной длины в строки другой длины, но в этом случае придётся уделять внимание различиям в размерности. Далее введём множество всех функций, выполняющих отображение $\{0,1\}^n \rightarrow \{0,1\}^n$ и обозначим его $\text{Func}_n$ .

Рассмотрим мощность этого множества. Очевидно, что $|{\text{Func}_n}| = 2^{n2^n}$ .

Если всё-таки не очевидно

$\text{Всего различных строк длины } n \space - \space 2^n.$ $\text{ Чтобы хранить } 2^n \text{ строк понадобится } n2^n \text{ бит.}$ $\text{Эти } n2^{n} \text{ бит и будут задавать искомое отображение } 2^n \text{ строк.}$ $\text{И всего таких отображений будет } 2^{n2^n}.$

Теперь мы можем определить случайную функцию. Случайная функция это любая случайно выбранная функция из $\text{Func}_n$ . Проще говоря, мы берём наши 2^n строк и каждой сопоставляем какую-то из тех же 2^n строк. Причем сопоставление происходит с равномерным распределением, то есть

$P(f(x)=y_0)=2^{-n}$

Где функция из $\text{Func}_n$ , а y_0 фиксированная точка.

Псевдослучайность

Интуитивно, псевдослучайность это что-то выглядящее, как случайность. И формальное определение так и вводится, только похожесть псевдослучайной функции на случайную определяется строго.

Давайте выпишем несколько равенств, верных для случайной функции:

$P(f(x) \in \{ \forall y:первый \space бит = 1 \}) = \frac{1}{2}$

Почти то же самое, но для наших целей вполне сгодится:

$P(f(x) \in \{ \forall y:последний \space бит = 1 \}) = \frac{1}{2}$

Для чётных можно выписать следующее:

$P(f(x) \in \{ \forall y:число \space нулей= число \space единиц \}) = \frac{1}{2^n} \begin{pmatrix} n \\ n/2 \end{pmatrix}$

Где $\begin{pmatrix} n \\ n/2 \end{pmatrix}$ число сочетаний из по n/2 (нужно выбрать n/2 позиций из возможных).

Подобных равенств можно выписать очень много. Скажем, к примеру, что мы придумали 20 таких равенств. Назовём их тестами и обозначим следующим образом:

Тогда можно определить псевдослучайною функцию, как функцию, которая удовлетворяет тестам с заданной точностью $\varepsilon$ :

$|P(A_i(f(x))=1)-P(A_i(F(x))=1)| < \varepsilon$

Где f(x) случайная функция, а F(x) функция, которую мы тестируем.

Но у такого определения есть существенный минус. Что если у кул-хацкера, который пытается вытащить полезную информацию из результата работы псевдослучайной функции, есть тест, которого нет у нас? Вероятно, для него эта функция окажется не такой уж и случайной. Поэтому введём несколько иное определение псевдослучайной функции.

Назовём функцию $(t,\varepsilon)$ -псевдослучайной, если для любого теста с полиномиальной сложностью, выполнение которого занимает времени не более чем верно

$|P(A(f(x))=1)-P(A(F(x))=1)| < \varepsilon$

Семейства

Окей, мы поняли, что такое случайная функция, что такое псевдослучайная функция, но никаких семейств так и не видно. На самом деле они уже здесь, нам достаточно взять некоторое количество псевдослучайных функций, удовлетворяющих нашим условиям, обозвать их F_k и семейство готово:

Семейство псевдослучайных функций это эффективно вычислимая функция двух переменных F_k(x)=F(k,x) , такая, что $\{0,1\}^m \times \{0,1\}^n \rightarrow \{0,1\}^l$ , где каждая из F_k является псевдослучайной. Переменная называется ключом функции.

Положим далее m=l=n .

Стоит отметить, что выбор конкретного эквивалентен выбору конкретной функции из семейства.

В начале статьи мы обсудили множество всех функций выполняющих отображение $\{0,1\}^n \rightarrow \{0,1\}^n$ и обозначили его $\text{Func}_n$ . Так вот, получается что семейство F_k задаёт распределение над множеством $\text{Func}_n$ .

Определение, данное выше, можно переформулировать в более привычный вид, в котором оно в основном встречается в статьях и учебниках:

F_k называется семейством псевдослучайных функций, если для случайного ни один эффективный алгоритм с полиномиальной временной сложностью не сможет отличить F_k от $f \in \text{Func}_n$ .

Наглядное пояснение

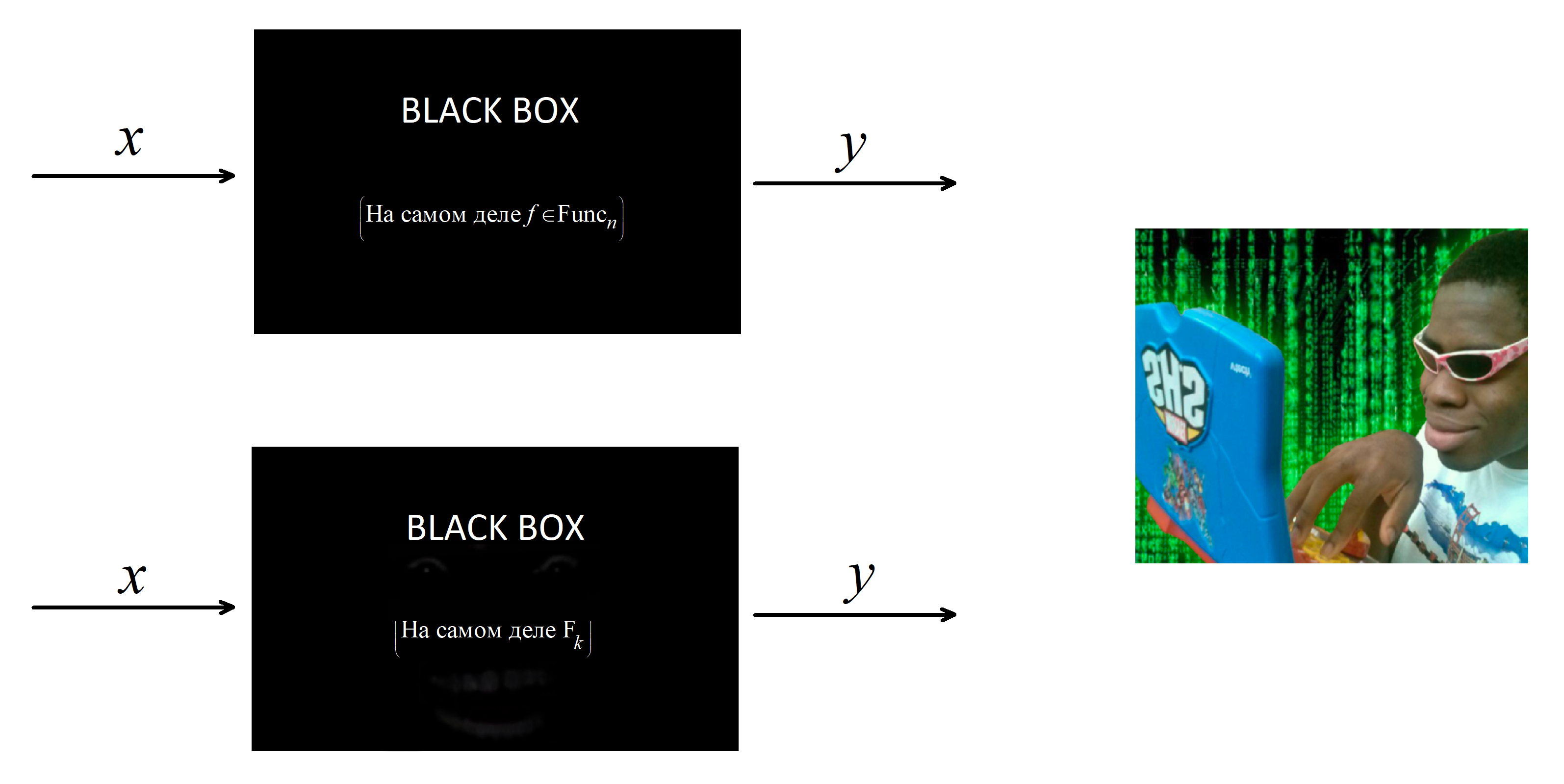
Вероятно, так будет проще осознать, что же в конечном итоге представляет из себя это семейство. Пусть есть две черных коробки, которые могут принимать на вход битовые строки и в ответ выдавать какие-то другие битовые строки. Примем, что на входе и на выходе коробок строки имеют определённую одинаковую длину. Отмечу, что выход этих коробок определяется только строкой на входе. То есть не может быть такого, что мы подали на вход какой-то коробки x_0 и на выходе получили y_0 , а потом, через некоторое время, мы снова подали на вход x_0 , но на выходе получили $y_1 \neq y_0$ . Пусть также есть злой хацкер, которому позарез нужно понять, какая из этих двух коробок скрывает в себе труЪ-случайную функцию, а какая просто притворяется. Этот хацкер может делать с этими коробками всё, что угодно. То есть подавать строки и считывать. Так вот, если тот, кто придумывал F_k , сделал всё правильно, то при случайно выбранном у хацкера ничего не выйдет (за вменяемое время).

PRF vs. PRG

PRG это псевдослучайный генератор. Звучат названия достаточно похоже, но путать их не стоит. Эти два понятия можно связать, получив из PRG PRF, а из PRF PRG. Почитать подробно, что такое PRG, можно тут. Если вкратце, то PRG это эффективно вычислимая функция (алгоритм), принимающая на вход случайную битовую строку длины (seed) и выдающая псевдослучайную битовую строку длины m>n . Почитать про то, как получить из PRG семейство псевдослучайных функций с доказательством того, что полученная конструкция действительно PRF можно в работе, упомянутой в самом начале статьи. А вот в обратную сторону всё намного проще. Достаточно положить

Где операция конкатенации, и мы получим простейший пример получения PRG из PRF. Очевидно, что подобных примеров можно придумать очень много. Отсюда напрашивается логичный вывод, что PRF понятие более мощное, нежели PRG.

Про блочные шифры

Наделив нашу PRF F_k парой дополнительных свойств мы получим ещё одну интересную абстракцию, называемою псевдослучайными перестановками. Для того, чтобы стать семейством псевдослучайных перестановок, F_k должна быть биективной и эффективно вычислимой в обоих направлениях для всех значений . То есть задача вычисления $F^{-1}(y)$ должна иметь единственный верный ответ и не должна составлять для нас особого труда.

Здесь уже можно догадаться, причём же тут блочные шифры. По сути, псевдослучайная перестановка представляет из себя ядро блочного шифра: мы берём исходное сообщение, разбиваем его на блоки длины , применяем к каждому из блоков F_k , где известно и отправителю и получателю, и затем отправляем наше сообщение, которое на данном этапе выглядит как набор случайных (псевдослучайных) битов.

В качестве примера блочного шифра, использующего псевдослучайные перестановки, можно привести AES.

Конец

На этом я закончу свою статью. Спасибо большое всем, кто дочитал.

P.S. Случайности не случайны. Случайностей вообще нет, развитие вселенной было определено ещё на момент её появления. Не воспринимайте это в серьёз, пожалуйста c:

P.P.S. Кто нашёл пасхалку большой молодец.

Материалы

How to Construct Random Functions тык

Pseudorandom Functions: Three Decades Later тык

Introduction to Modern Cryptography тык

Pseudorandom Functions and Block Ciphers тык

Подробнее..

Категории: Информационная безопасность , Научно-популярное , Математика , Случайность , Псевдослучайность , Блочный шифр , Псевдослучайные генераторы

Перевод Как и почему компьютеры кидают шулерские кости

20.07.2020 18:22:00 |

Автор: admin

Исследователи на один шаг ближе подошли к добавлению вероятностных процессов к детерминистским машинам

Давняя проблема компьютеров симуляция броска шулерского кубика

Вот вам обманчиво простое упражнение: придумайте случайный номер телефона. Семь цифр подряд, выбранных так, чтобы каждая из них была одинаково вероятной, и так, чтобы ваш выбор очередной цифры не влиял на выбор следующей. Скорее всего, у вас этого не выйдет. Можете не верить мне на слово исследования, проводимые ещё с 1950-х годов, показывают, насколько мы неслучайны с математической точки зрения, даже не осознавая этого.

Не расстраивайтесь. Компьютеры тоже не генерируют случайных чисел. Они и не должны программы и аппаратура компьютеров работают на булевой логике, а не на вероятностях. Компьютерная культура зиждется на детерминизме, сказал Викаш Мансинхка, руководящий проектом вероятностных вычислений в Массачусетском технологическом институте, и это проявляется практически на всех уровнях.

Однако программисты хотят создавать программы, работающие со случайностью иногда того требуют задачи. За все эти годы были разработаны хитроумные алгоритмы, которые, хотя и не генерируют случайных чисел, предлагают хитрые и эффективные способы использования и манипулирования случайностью. Одну из самых новых попыток предприняла группа Мансинхки в MIT, которая собирается представлять свой алгоритм Fast Loaded Dice Roller [быстрый бросок шулерских кубиков], или FLDR, на международной конференции по ИИ и статистике в августе.

Проще говоря, FLDR использует случайную последовательность для идеальной симуляции броска шулерского кубика (или монеты с нарушенной развесовкой, или краплёных карт). Он показывает, как превратить идеально случайный бросок монеты в искажённый, сказал математик Питер Бирхорст из Ново-орлеанского университета. Бирхорст не участвовал в этом исследовании, однако считает предпосылки, лежащие в основе FLDR, убедительными.

FLDR не даст вам преимуществ при игре в Монополию или на столах для игры в крэпс в Лас-Вегасе. Однако его создатели говорят, что он позволяет интегрировать случайные числа в изначально детерминистское ПО или железо. Включение подобных неопределённостей поможет машинам делать предсказания, больше похожие на человеческие, и лучше симулировать явления, основанные на случайности климат или финансовые рынки.

Случайность концепция более сложная, чем кажется. У каждой цифры в последовательности случайных цифр, где нет никакой различимой закономерности, вероятность появления одна и та же. К примеру, число не является случайным, однако считается, что по этому определению его цифры случайные (математики называют это нормальным): каждая цифра от 0 до 9 появляется примерно одно и то же количество раз.

И хотя в Google можно найти генераторы случайных чисел, чистой случайности там не будет. Сегодняшние процессоры, поисковые системы и генераторы паролей используют псевдослучайный метод, который достаточно хорошо подходит для большинства задач. Числа генерируются по сложным формулам однако, в теории, если знать формулу, то можно будет предсказать последовательность.

Учёные пытались встроить в машины реальную случайность не менее 80 лет. А до тех пор случайные номера брали у старых и надёжных помощников кидали кости, вынимали шары с номерами из хорошо перемешанного мешка, или использовали другие механические устройства. В 1927 году один статистик сделал выборку из данных по переписи населения, составив табличку из 40 000 случайных чисел.

Викаш Мансинхка, руководящий проектом вероятностных вычислений в Массачусетском технологическом институте

Ранними источниками случайных чисел были физические машины. Первый генератор случайных чисел изобрели британские статистики Морис Джордж Кендол и Бернард Бабингтон Смит, описавшие его в 1938 году. Машину ставили в тёмную комнату, и там она крутила диск, поделённый на 10 секторов, пронумерованных от 0 до 9. Когда кто-нибудь жал на кнопку через неравные промежутки времени, краткие вспышки неона или искры освещали диск, выхватывая из темноты его, казалось, застывшее изображение, где было видно только одну цифру. Более поздняя машина, Эрни, использовала шум в неоновых трубках. С 1957 года она выбирала выигрышные номера в британской лотерее.

Позднее в поисках истинно случайных последовательностей специалистам по информатике, по словам Бирхорст, пришлось обращаться к таким природным явлениям, как реликтовое излучение или непредсказуемые квантовые системы. В природе существуют истинно непредсказуемые случайные процессы, которыми можно воспользоваться, сказал он. Электрон, отражающийся влево или вправо, заранее не может сказать, что он сделает.

Однако на одной случайности далеко не уедешь. К концу 1940-х физики начали генерировать случайные числа, укладывающиеся в заданное распределение вероятности. Такие инструменты теоретические версии ШУ кубиков точнее работали в реальных ситуациях, типа загруженности дорог или химических реакций. К 1976 году пионеры информатики Дональд Кнут и Эндрю Яо представили алгоритм, способны на основе последовательности случайных чисел выдавать случайные выборки любого массива взвешенных результатов. Это наиболее эффективный по времени алгоритм из всех, что можно придумать, сказал Фера Саад, аспирант из лаборатории Мансинхка, руководивший работой над FLDR.

К сожалению, как говорит Саад, алгоритм идёт на компромисс, известный среди специалистов по информатике: многие быстро работающие приложения используют большое количество памяти, а приложения, использующие немного памяти, могут работать очень долго. Алгоритм Кнута и Яо попадает в первую категорию, что делает его элегантным, но слишком требовательным к памяти для практического применения.

Однако прошлой весной Саад придумал хитрый ход. Он понял, что если сумма весов ждя цифр кубика равна какой-нибудь степени 2, алгоритм получается эффективным и по памяти, и по времени. Представим, что для кубика с шестью гранями к вероятностям выкинуть цифры от 1 до 6 добавили веса 1, 2, 3, 4, 5 и 1. То есть, вероятность выкинуть 1 составляет 1/16, а 2 2/16. В итоге сумма весов составляет 16 или 2⁴ и алгоритм получается эффективным и по памяти, и по времени.

Фера Саад, аспирант из MIT

Но допустим, веса будут равняться 1, 2, 3, 2, 4, 2, что в сумме даст 14. Поскольку 14 это не степень 2, алгоритму Кнута-Яо потребуется значительно больше памяти. Саад понял, что можно добавить дополнительный вес так, чтобы веса всегда давали в сумме степень 2. В данном случае можно добавить вымышленную грань с весом 2, и тогда веса в сумме дадут 16. Если алгоритм выбирает реальную грань, это значение записывается. Если вымышленную значение отбрасывается, и алгоритм запускается снова.

Это ключевой момент эффективности FLDR, делающий его мощным инструментом для симуляций. Количество дополнительной памяти для дополнительных бросков незначительно по сравнению с большими объёмами, требовавшимися первоначальной версии алгоритма.

FLDR делает алгоритм Кнута-Яо эффективным и предоставляет возможность расширить его область применения. Симуляции изменения климата, предсказания урожаев, симуляции поведения частиц, модели финансовых рынков и обнаружение подземных ядерных взрывов всё это зависит от случайных чисел, распределённых со взвешенной вероятностью. Также случайные числа лежат в основе криптографических схем, защищающих данные, передаваемые по интернету.

Мансинхка говорит, что FLDR может помочь исследователям находить способы интегрировать вероятность в компьютерные процессоры этим занимается его лаборатория в MIT. Алгоритм может помочь улучшить программные библиотеки и новую архитектуру процессоров, которые смогут генерировать случайные числа и эффективно их использовать. Это значительно изменило бы ситуацию по сравнению с теми детерминистскими булевыми машинами, к которым мы привыкли.

У нас, возможно, есть хороший шанс интегрировать случайность в строительные блоки программ и железа, сказал он.

Подробнее..

Категории: Программирование , Случайность , Детерминизм , Fldr

Recovery mode Звездный год (365 дней 369 минут), Тропический год( 348.5 минут) и звездные сутки(1436 минут) в радиоактивном распаде

01.01.2021 00:16:35 |

Автор: admin

В этой статье будет приведен очень короткий код поиска периодов тропического года, звездного года и звездных суток в данных радиоактивного распада плутония.

Вот здесь на GitHub.com можно скачать все данные и код

Всего данные по почти 19 дней одного года days.dat
И 2 дня в мае 2005 года 0505.txt
И 2 дня в мае 2006 года 0506.txt

Средняя продолжительность тропического года по весеннему равноденствию это на Января 1, 2000 365.2421897 или 365 дней, 5 часов, 48 минут, 45.19 секунд.
Звездный год это 365 дней и 369 минут
Звездные сутки 1436 минут движение Земли в течении которого планета совершает полный оборот относительно сферы неподвижных звезд.

Загружаем данные и расфасовываем по рядам по 60 значений

import mathimport randomfrom statistics import meankoeff=60;matrix = [line.strip() for line in open('/users/andrejeremcuk/downloads/0505.txt')];matrix1 = [line.strip() for line in open('/users/andrejeremcuk/downloads/0506.txt')];matrixd = [line.strip() for line in open('/users/andrejeremcuk/downloads/days.dat')];arra=[[ 0 for e in range(koeff)] for t in range(int(len(matrix)/koeff))];harra=[0 for t in range(int(len(matrix)/koeff))];arra1=[[ 0 for e in range(koeff)] for t in range(int(len(matrix)/koeff))];harra1=[0 for t in range(int(len(matrix)/koeff))];arrad=[[ 0 for e in range(koeff)] for t in range(int(len(matrixd)/koeff))];harrad=[0 for t in range(int(len(matrixd)/koeff))];for i in range(len(matrix)): matrix[i]=int(matrix[i]);matrix1[i]=int(matrix1[i]);for i in range(len(matrixd)): matrixd[i]=int(matrixd[i]);

Сортируем функцией sorted по возрастанию

z=0;for jk in range(int(len(matrix)/koeff)): #int(len(matrix)/koeff) for mk in range(koeff): arra[jk][mk]=float(matrix[z]);arra1[jk][mk]=float(matrix1[z]);z=z+1;for jk in range(int(len(matrix)/koeff)): harra[jk]=sorted(arra[jk]);harra1[jk]=sorted(arra1[jk])z=0;for jk in range(int(len(matrixd)/koeff)):  for mk in range(koeff): arrad[jk][mk]=float(matrixd[z]);z=z+1;for jk in range(int(len(matrixd)/koeff)): harrad[jk]=sorted(arrad[jk]);

Делим на среднее значение

for jk in range(int(len(matrix)/koeff)):  average=mean(harra[jk]) for mk in range(koeff): harra[jk][mk]=harra[jk][mk]/average average1=mean(harra1[jk]) for mk in range(koeff): harra1[jk][mk]=harra1[jk][mk]/average1for jk in range(int(len(matrixd)/koeff)):  averaged=mean(harrad[jk]) for mk in range(koeff): harrad[jk][mk]=harrad[jk][mk]/averaged

Далее привожу функцию сравнения:

import numpyimport numpy as npfrom numpy.fft import fft, fftfreqimport matplotlib.pyplot as pltfrom numpy import linspace, loadtxt, ones, convolvefrom numpy import array, zeros, argmin, inffrom numpy.linalg import normdef _trackeback(D):    i, j = array(D.shape) - 1    p, q = [i], [j]    while (i > 0 and j > 0):        tb = argmin((D[i-1, j-1], D[i-1, j], D[i, j-1]))        if (tb == 0):            i = i - 1            j = j - 1        elif (tb == 1):            i = i - 1        elif (tb == 2):            j = j - 1        p.insert(0, i)        q.insert(0, j)    p.insert(0, 0)    q.insert(0, 0)    return (array(p), array(q))def dtw(dr):    r, c = len(dr), len(dr[0]);    D = zeros((r + 1, c + 1));    D[0, 1:] = inf    D[1:, 0] = inf    for i in range(r):        for j in range(c):            D[i+1, j+1] = dr[i][j];    for i in range(r):        for j in range(c):            D[i+1, j+1] += min(D[i, j], D[i, j+1], D[i+1, j])    D = D[1:, 1:];    dist = D[-1, -1] / sum(D.shape);    return dist, D, _trackeback(D)

def stat(x,y):    pikk=[[float("inf") for m in range(len(y))] for t in range(len(x))];    for e in range(len(x)):     for l in range(len(y)): pikk[e][l]=(((abs(x[e]-y[l])))*(abs(e-l)+1));    dt=dtw(pikk)    p1=dt[2][0];p=dt[2][1];    res=0;uj=0;rmu=0;    for e in range(len(p)):      for l in range(len(p1)):      pl=p[l];pe=p[e];ml=p1[l];me=p1[e];        #pl=l;pe=e;ml=l;me=e;        ret=0;re=1;rea=0;red=0;ab=abs(y[pl]-y[pe]);ac=(pe-pl);rmt=abs(1-x[ml]/y[pl]);rmr=abs(1-x[me]/y[pe]);      au=abs(x[ml]-x[me]);ao=(me-ml);hip=math.sqrt(ab**2+ac**2);hipe=math.sqrt(ao**2+au**2);      if (1<ml<58)&(1<pl<58)&(1<me<58)&(1<pe<58):              rea=abs(1-abs(abs(y[pl-1]*y[pl]*y[pl+1]*y[pl+2])/y[pl]**4))+abs(1-abs((y[pe-1]*y[pe]*y[pe+1]*y[pe+2])/y[pe]**4))       rea+=abs(1-abs(abs(x[ml-1]*x[ml]*x[ml+1]*x[ml+2])/x[ml]**4))+abs(1-abs((x[me-1]*x[me]*x[me+1]*x[me+2])/x[me]**4))      else: rea=0;      if (hip!=0)and(hipe!=0):        if (math.asin(abs(au)/hipe)!=0)&(math.asin((ab)/hip)!=0):        red=0+abs(1-abs(math.asin((ab)/hip)/math.asin((au)/hipe)));        red+=abs(1-abs(math.asin((au)/hipe))/math.asin((ab)/hip));      if (x[me]!=0)and(y[pe]!=0)and(x[ml]!=0)and(y[pl]!=0):        ret=0+abs(1-abs((0.00+abs(float(y[pl])/float(y[pe])))/(0.00+abs(float(x[ml])/float(x[me])))));       ret+=abs(1-abs((float(x[ml])/float(x[me]))/(float(y[pl])/float(y[pe]))));      re=1+abs(1-abs(float(abs(pe-pl)+1))/float(abs(me-ml)+1));rme=(y[pe]+0)+(y[pl]+0)+(x[me]+0)+(x[ml]+0);rmu+=rme;      #print(rme);      #print(rea,red,ret,re,(abs(e-l)+1),rme);      if rea==0: rea=1;      res+=abs(ret*red*red*rea)*(abs(e-l)+1)*rme*re;uj=uj+1;     if uj==0: uj=1;    return res/uj#/rmu#*rmu *(abs(x[ml]-y[pe])+0.01)         *(abs(x[ml]-y[pe])+abs(x[me]-y[pl]))

Далее пример кода сравнения 1440 раз всех графиков с отступом от 0 до +1440 минут 2005 и 2006 года:

def dist(rast):    statistic=0;statis=0;    for i in range(1440):     jk=i+000;x=harra1[jk];y=harra[jk+rast];     rt=stat(x,y);     statistic+=rt;     jk=i+000;x=harra[jk];y=harra1[jk+rast];     rt=stat(x,y);     statis+=rt;    return statis,statistic;d=[];for i in range(1440):  print(i); d.append((dist(i),i)); print(d[-1]);d004=[];for i in range(len(d)): t4=int(d[i][0][0]+d[i][0][1])/2 d004.append(t4)import numpynumpy.argsort(d004)

Для данных за 2 суток я исследовал окрестности +1440 минут

>>> for i in range(len(d1)):

... print(d01[i],1440-i)

...

1529.0 1440

1499.0 1439

1510.0 1438

1530.5 1437

`1439.5 1436`



1534.5 1435

1516.0 1434

1473.0 1433

1503.0 1432

1486.0 1431

1514.5 1430

1507.5 1429

1525.0 1428

1460.0 1427

1558.5 1426

1562.5 1425

1495.0 1424

1511.0 1423

1527.5 1422

1507.0 1421

1506.0 1420

1498.0 1419

1517.0 1418

1471.0 1417

1478.0 1416

1588.0 1415

1513.5 1414

>>> import numpy

>>> numpy.argsort(d01)

array([ 38, 4, 78, 71, 59, 76, 13, 101, 74, 83, 41, 90,
23,

7, 24, 9, 33, 48, 100, 70, 29, 54, 44, 91, 63, 103,

93, 87, 42, 32, 16, 97, 57, 30, 21, 61, 39, 1, 64,

77, 99, 49, 52, 8, 79, 95, 66, 51, 45, 20, 40, 27,

60, 19, 11, 86, 34, 92, 2, 88, 17, 85, 26, 10, 6,

81, 22, 36, 73, 58, 56, 50, 12, 65, 69, 18, 46, 0,

68, 84, 3, 67, 96, 5, 28, 102, 31, 55, 47, 43, 75,

98, 94, 35, 89, 14, 37, 15, 72, 53, 82, 62, 25, 80])

>>> d01[38]

1419.0

>>> d01[4]

1439.5

И вот результат второй минимум выпадает на +1436 минуту d01[4] -4 значение

>>> for i in range(70):

... print(d04[340+i])

...

(1444, 340)

(1451, 341)

(1531, 342)

(1433, 343)

(1495, 344)

(1460, 345)

(1494, 346)

(1489, 347)

(1460, 348)

(1492, 349)

(1491, 350)

(1499, 351)

(1477, 352)

(1499, 353)

(1431, 354)

(1520, 355)

(1481, 356)

(1454, 357)

(1530, 358)

(1496, 359)

(1443, 360)

(1434, 361)

(1450, 362)

(1470, 363)

(1493, 364)

(1485, 365)

(1428, 366)

(1491, 367)

(1516, 368)

`(1414, 369)`



(1521, 370)

(1452, 371)

(1455, 372)

`(1384, 373)`



(1525, 374)

(1395, 375)

(1436, 376)

(1430, 377)

(1478, 378)

(1457, 379)

(1444, 380)

(1429, 381)

(1476, 382)

(1608, 383)

(1499, 384)

(1439, 385)

(1467, 386)

(1466, 387)

(1516, 388)

(1471, 389)

(1471, 390)

(1456, 391)

(1472, 392)

(1442, 393)

(1435, 394)

(1495, 395)

(1476, 396)

(1484, 397)

(1474, 398)

(1489, 399)

(1422, 400)

(1440, 401)

(1477, 402)

(1489, 403)

(1494, 404)

(1472, 405)

(1541, 406)

(1469, 407)

(1522, 408)

(1444, 409)

Далее для звездного года. Тут надо определить что алгоритм сравнивает картинки коллективного взаимодействия, поэтому гистограмный метод находит 368 как абсолютный минимум. Здесь же 373 минута третья от конца 369 минута тоже локальный минимум и 348 минута.
Всего рассчитано до +1440 минут двух дней в 2005 и 2006 годах.

>>> sor=numpy.argsort(d004)

>>> sor[:90] # всего до sor[:1440]

array([ 137, 140, 373, 583, 2, 47, 375, 266, 709, 40,
439,

29, 751, 226, 245, 433, 217, 789, 437, 524, 659, 369,

124, 919, 954, 544, 76, 256, 103, 991, 419, 106, 323,

400, 606, 626, 120, 99, 259, 321, 11, 1369, 235, 366,

158, 1258, 240, 381, 176, 118, 491, 377, 207, 354, 123,

825, 415, 167, 897, 588, 865, 46, 1129, 343, 60, 97,

842, 361, 211, 394, 628, 435, 1218, 878, 268, 376, 153,

165, 880, 494, 643, 609, 1439, 301, 85, 107, 252, 385,

173, 455])

Подробнее..

Категории: Научно-популярное , Алгоритмы , Python , Математика , Data mining , Случайность , Радиоактивность , Вероятность

	Русский
	English

Случайность

Случайности не случайны кто такие семейства псевдослучайных функций (PRFs)

Случайность

Псевдослучайность

Семейства

Наглядное пояснение

PRF vs. PRG

Про блочные шифры

Конец

Перевод Как и почему компьютеры кидают шулерские кости

Исследователи на один шаг ближе подошли к добавлению вероятностных процессов к детерминистским машинам

Recovery mode Звездный год (365 дней 369 минут), Тропический год( 348.5 минут) и звездные сутки(1436 минут) в радиоактивном распаде

1439.5 1436

(1414, 369)

(1384, 373)

Категории

Последние комментарии

`1439.5 1436`

`(1414, 369)`

`(1384, 373)`