Кривые

Равномерное перемещение объекта вдоль кривой

27.07.2020 18:22:43 |

Автор: admin

В процессе разработки игры в совершенно различных жанровых категориях может возникнуть потребность запустить какой-либо игровой объект вдоль гладкой кривой с постоянной или контролируемой скоростью, будь то грузовик, следующий из города А в город Б, выпущенная по хитрой траектории ракета, или самолет противника, выполняющий заложенный манёвр.

Наверное, каждый имеющий отношение к теме знает или, по крайней мере, слышал, про кривые Безье, B-сплайны, сплайны Эрмита и прочие интерполяционные и сглаживающие сплайны и совершенно правильно предложил бы использовать в описанной ситуации один из них, но не всё так просто, как хотелось бы.

В нашем случае сплайн это функция, отображающая набор входных параметров (контрольные точки) и значение аргумента $inline$ (обычно принимающего значения от 0 до 1) в точку на плоскости или в пространстве. Получившаяся кривая это множество значений функции-сплайна при $t\in[0,1]$ .

В качестве примера можно рассмотреть кубическую кривую Безье, которая задаётся следующим уравнением:

Кубическая кривая Безье

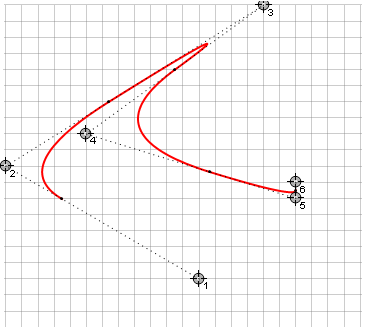
На рисунке изображены две кубических кривые Безье, задаваемых четырьмя точками (через две из них кривая проходит, оставшиеся две задают кривизну).

Анимация отображения параметра t в точку кривой

Для того, чтобы из участков кривых построить более сложный и вариативный маршрут, их можно соединить по цепочке, оставляя одну общую точку-звено:

Кусочный сплайн

С заданием и параметризацией маршрута разобрались, теперь переходим к основному вопросу. Чтобы наш условный самолёт двигался вдоль маршрута с постоянной скоростью, нам нужно в любой момент времени уметь вычислять точку на кривой в зависимости от пройденного вдоль этой кривой расстояния $inline$ , при этом имея лишь возможность вычислить положение точки на кривой по значению параметра $inline$ (функцию $inline$ ). Именно на этом этапе начинаются сложности.

Первой мыслью было сделать линейное отображение $len\in[0, Length] \Rightarrow t\in[0,1]$ и вычислить $inline$ от получившегося значения легко, вычислительно дёшево, в общем, то, что нужно.

Проблема данного способа очевидна сразу же на самом деле пройденная дистанция $inline$ зависит от $inline$ нелинейно, и чтобы в этом убедиться достаточно расставить по маршруту равномерно распределенные по значению $inline$ точки:

Равномерно распределенные по пути точки

Самолёт будет замедляться на одних участках и ускоряться на других, чем делает данный способ параметризации кривой совершенно неприменимым для решения описанной задачи (самолёт выбран исключительно в качестве наглядного примера и цель описать его движение физически корректным способом не преследовалась):

Визуализация неправильной параметризации кривой

Обратившись за советом в поисковик, на stackoverflow и youtube, я обнаружил второй способ вычисления $inline$ , а именно представление кривой в виде кусочно-линейной функции (расчета набора равноудаленных друг от друга по кривой точек):

Представление кривой в виде кусочно-линейного сплайна

Процедура эта итеративная: берется небольшой шаг по $inline$ , с ним движемся по кривой, суммируя пройденное расстояние как длину кусочно-линейного сплайна до тех пор, пока не будет пройдено заданное расстояние, после чего точка запоминается, а процесс возобновляется.

Пример кода

Источник

public Vector2[] CalculateEvenlySpacedPoints(float spacing, float resolution = 1)  {    List<Vector2> evenlySpacedPoints = new List<Vector2>();    evenlySpacedPoints.Add(points[0]);    Vector2 previousPoint = points[0];    float dstSinceLastEvenPoint = 0;    for (int segmentIndex = 0; segmentIndex < NumSegments; segmentIndex++)    {      Vector2[] p = GetPointsInSegment(segmentIndex);      float controlNetLength = Vector2.Distance(p[0], p[1]) + Vector2.Distance(p[1], p[2]) + Vector2.Distance(p[2], p[3]);      float estimatedCurveLength = Vector2.Distance(p[0], p[3]) + controlNetLength / 2f;      int divisions = Mathf.CeilToInt(estimatedCurveLength * resolution * 10);      float t = 0;      while (t <= 1)      {        t += 1f/divisions;        Vector2 pointOnCurve = Bezier.EvaluateCubic(p[0], p[1], p[2], p[3], t);        dstSinceLastEvenPoint += Vector2.Distance(previousPoint, pointOnCurve);        while (dstSinceLastEvenPoint >= spacing)        {          float overshootDst = dstSinceLastEvenPoint - spacing;          Vector2 newEvenlySpacedPoint = pointOnCurve + (previousPoint - pointOnCurve).normalized * overshootDst;          evenlySpacedPoints.Add(newEvenlySpacedPoint);          dstSinceLastEvenPoint = overshootDst;          previousPoint = newEvenlySpacedPoint;        }        previousPoint = pointOnCurve;      }    }    return evenlySpacedPoints.ToArray();  }

И, вроде бы, задача решена, ведь можно разбить маршрут на очень много отрезков и радоваться тому, как плавно и размеренно движется объект, так как вычисление точки на кусочно-линейной функции дело простое и быстрое. Но у такого подхода тоже есть довольно очевидные недостатки, которые не давали мне покоя довольно затратная процедура изменения шага разбиения или геометрии кривой и необходимость поиска баланса между точностью (большее потребление памяти) и экономией памяти (становится более заметной ломаность маршрута).

Вследствие чего я продолжил поиски и наткнулся на отличную статью Moving Along a Curve with Specified Speed, на основе которой строятся дальнейшие рассуждения.

Значение скорости можно вычислить как $\sigma(t) = |V(t)|=|\frac{dX}{dt}|$ , где $inline$ функция сплайна. Чтобы решить поставленную задачу, нужно найти функцию $inline$ , где $inline$ длина дуги от начальной точки до искомой, и это выражение устанавливает соотношение между $inline$ и $inline$ .

Используя замену переменной дифференцирования, мы можем записать

$\frac{dY}{dt}=\frac{dX}{ds}\frac{ds}{dt}.$

Учитывая, что скорость величина неотрицательная, получаем

$|\frac{dY}{dt}|=|\frac{dX}{ds}||\frac{ds}{dt}|=\frac{ds}{dt},$

так как $|\frac{dX}{ds}| = 1$ по условию неизменности модуля вектора скорости (вообще говоря, $|\frac{dX}{ds}|$ равен не единице, а константе, но для простоты выкладок примем эту константу равной единице).

Теперь получим соотношение между $inline$ и $inline$ в явном виде:

$s=g(t)=\int_{0}^{t}|\frac{dY(\tau)}{dt}|d\tau,$

откуда полная длина кривой $inline$ , очевидно, вычисляется как $inline$ . С помощью полученной формулы можно, имея значение аргумента $inline$ , вычислить длину дуги до точки, в которую это значение $inline$ отображается.

Нас же интересует обратная операция, то есть вычисление значения аргумента $inline$ по заданной длине дуги $inline$ :

$t=g^{-1}(s).$

Так как не существует общего аналитического способа нахождения обратной функции, придется искать решение численное. Обозначим $inline$ При заданном $inline$ , требуется найти такое значение $inline$ , при котором $inline$ . Таким образом, задача превратилась в задачу поиска корня уравнения, с чем может прекрасно справиться метод Ньютона.

Метод образует последовательность приближений вида

$t_{i+1}=t_i-\frac{F(t_i)}{F'(t_i)},$

где

$F'(t)=\frac{dF}{dt}=\frac{dg}{dt}=|\frac{dY}{dt}|.$

Для вычисления $inline$ требуется вычислить $inline$ , вычисление которого, в свою очередь, требует численного интегрирования.

Выбор $t_0=\frac{s}{L}$ в качестве начального приближения теперь выглядит разумным (вспоминаем первый подход к решению задачи).

Далее выполняем итерации методом Ньютона до тех пор, пока погрешность решения не станет приемлемой, либо количество проделанных итераций непозволительно большим.

При использовании стандартного метода Ньютона потенциально может возникнуть проблема. Функция $inline$ неубывающая, так как её производная $inline$ неотрицательна. Если вторая производная $inline$ , то функцию называют выпуклой и метод Ньютона на ней гарантированно сходится к корню. Однако, в нашем случае, $inline$ может оказаться отрицательной, из-за чего метод Ньютона может сойтись за пределами диапазона определения $t\in[0,1]$ . Автор статьи предлагает использовать модификацию метода Ньютона, которая, в случае если очередной результат итерации методом Ньютона не попадает в текущий ограничивающий корень интервал, вместо него выбирает середину интервала (метод дихотомии). Вне зависимости от результата вычисления на текущей итерации, диапазон сужается, а значит, метод сходится к корню.

Остается выбрать метод численного интегрирования я воспользовался квадратурами метода Гаусса, так как он обеспечивает достаточно точный результат при небольших затратах.

Код функции, вычисляющей t(s)

public float ArcLength(float t) => Integrate(x => TangentMagnitude(x), 0, t);private float Parameter(float length){  float t = 0 + length / ArcLength(1);  float lowerBound = 0f;   float upperBound = 1f;  for (int i = 0; i < 100; ++i)  {    float f = ArcLength(t) - length;    if (Mathf.Abs(f) < 0.01f)      break;    float derivative = TangentMagnitude(t);    float candidateT = t - f / derivative;    if (f > 0)    {      upperBound = t;      if (candidateT <= 0)        t = (upperBound + lowerBound) / 2;      else        t = candidateT;    }    else    {      lowerBound = t;      if (candidateT >= 1)        t = (upperBound + lowerBound) / 2;      else        t = candidateT;    }  }  return t;}

Код функции численного интегрирования

private static readonly (float, float)[] CubicQuadrature ={(-0.7745966F, 0.5555556F), (0, 0.8888889F), (0.7745966F, 0.5555556F)};public static float Integrate(Func<float, float> f, in float lowerBound, in float uppedBound){  var sum = 0f;  foreach (var (arg, weight) in CubicQuadrature)  {    var t = Mathf.Lerp(lowerBound, uppedBound, Mathf.InverseLerp(-1, 1, arg));    sum += weight * f(t);  }  return sum * (upperBound - lowerBound) / 2;}

Далее можно настроить погрешность метода Ньютона, выбрать более точный метод численного интегрирования, но задача, по сути, решена был построен алгоритм вычисления аргумента $inline$ сплайна для заданной длины дуги. Для объединения нескольких участков кривых в один и написания обобщенной процедуры вычисления $inline$ можно хранить длины всех участков и предварительно вычислять индекс участка, на котором требуется произвести итеративную процедуру модифицированным методом Ньютона.

Равномерно распределенные вдоль пути точки

Теперь самолет движется равномерно

Таким образом, нами были рассмотрены несколько способов параметризации сплайна относительно пройденного расстояния, в использованной мной в качестве источника статье в качестве варианта автор предлагает численно решать дифференциальное уравнение, но, по его собственной ремарке, предпочитает модифицированный метод Ньютона:

I prefer the Newtons-method approach because generally t can be computed faster than with differential equation solvers.

В качестве заключения приведу таблицу времени расчета положения точки на представленной на скриншотах кривой в одном потоке на процессоре i5-9600K:

Кол-во вычислений	Среднее время, мс
100	0,62
1000	6,24
10000	69,01
100000	672,81

Считаю, что такая скорость вычислений вполне позволяет применять их в различных играх и симуляциях. Буду рад уточнениям и критике по существу в комментариях.

Подробнее..

Категории: Алгоритмы , C , Математика , Разработка игр , Геймдев , Unity , Численные методы , Кривые , Метод ньютона , Метод гаусса

Циркулярные кривые 2-го порядка

01.09.2020 20:19:15 |

Автор: admin

Как известно, кривыми Безье нельзя построить дугу окружности или эллипса. В этой статье рассматриваются кривые, лишённые такого недостатка.

Кривые Безье

Логика построения кривых Безье хорошо понятна из следующей анимации:

Чтобы получить формулу непосредственно из графического представления, достаточно определить вспомогательную функцию для линейной интерполяции между двумя точками, в которая при изменении параметра t от 0 до 1 возвращает промежуточные значения от a до b:

$display$

Примечание

В математике как-то не сложилось устойчивого названия для функции линейной интерполяции и в зависимости от сферы применения она может называться lerp, blend, mix и как-то ещё. К ней также относится и кривая Безье первого порядка.

С её помощью можно последовательно найти необходимые точки сначала найти

$display$

а затем уже через них найти

$display$

При желании, можно подставить функции друг в друга и сократить хотя это особо и не упростит вычисления, зато позволит обобщить кривые на произвольное количество опорных точек (через полиномы Бернштейна). В нашем случае получим

$display$

Увеличение порядка кривых достигается тривиально исходные точки задаются не константно, а как результат интерполяции между n+1 других контрольных точек:

Примечание

В этих формулах в качестве точек могут выступать как комплексные числа, так и векторы произвольной размерности. Дальнейшие формулы будут корректными только для комплексных чисел.

Циркулярные кривые

Дуга окружности

Чтобы похожим образом построить дугу окружности, необходимо определить соответствующую логику построения по аналогии с черчением окружности циркулем.

Изначально нам неизвестен центр окружности d он находится через пересечение перпендикуляров к касательным в точках a и b (далее узловых); сами же касательные задаются с помощью точки c (далее направляющей). Для построения произвольной дуги окружности (меньшей 180) достаточно, чтобы расстояния от направляющей точки до узловых были одинаковыми.

Дуга эллипса

Построить дугу эллипса уже посложнее потребуется два вектора, вращающихся в разные стороны (подробнее здесь)

Используя озвученный выше способ нахождения точки d, мы уже не можем построить произвольную дугу эллипса только лишь от 0 до 90 (в том числе и повёрнутую на некоторый угол).

Дуга гипотрохоиды

Задав условие, что в начале и конце черчения векторы должны лежать на одной прямой, мы получим дугу гипотрохоиды во всех остальных случаях. Это условие не случайно и (помимо однозначного определения кривой) гарантирует совпадение касательных в узловых точках. Как следствие, угловые пути, которые проходят оба вектора, станут разными, но в сумме по-прежнему будут давать 180.

Как изменяется форма кривой в зависимости от положения направляющей точки, можно посмотреть на следующей анимации:

Алгоритм

Поскольку здесь мы имеем вращения на двумерной плоскости, математику построения этих кривых удобно описывать через комплексные числа.

1) находим точку пересечения нормалей касательных, проведённых от направляющей точки к узловым:

$d=\frac{(2 a-c) (c-b) a^*+ (2 b-c) (a-c) b^*-c (a-b) c^*}{(c-b)a^*+(a-c) b^*-(a-b) c^*}$

(здесь звёздочка означает комплексное сопряжение).

2) зная d, находим длины нормалей

$r_{\text{ad}}=\left| a-d\right|$

$r_{\text{bd}}=\left| b-d\right|$

и их сумму и разность

$r_m=\frac{1}{2} \left(r_{\text{ad}}+r_{\text{bd}}\right)$

$r_s=\frac{1}{2} \left(r_{\text{ad}}-r_{\text{bd}}\right)$

3) находим единичный вектор, от которого начинается построение

$v=\frac{a-d}{\left| a-d\right| }$

Примечание

в некоторых библиотеках для работы с комплексными числами и системах компьютерной алгебры для этого есть отдельная функция sign(x).

4) находим угловые пути, которые должны пройти каждый из векторов

$\phi _m=\arg \left(\frac{a-d}{b-d}\right)$

$\phi _s=\arg \left(-\frac{a-d}{b-d}\right)$

Примечание

При умножении векторов их длины умножаются, а углы складываются. Здесь деление используется для противоположной задачи найти разницу углов, т. е. угол между векторами.

Поскольку для функции аргумента длина вектора не играет роли, тот же результат можно получить и заменив деление умножением на комплексно сопряжённый вектор такой вариант даже предпочтительнее, поскольку будет более численно устойчив на очень малых значениях из-за отсутствия деления; здесь же выбор в пользу деления сделан исключительно ради наглядности.

Здесь имеется ещё один крайне важный момент. Если бы мы сначала нашли углы для каждого вектора по отдельности, а потом бы считали разницу как

$\arg (a-d)-\arg (b-d)$

результат не всегда был бы корректным из-за многозначности функции аргумента.

5) последовательно изменяя t от 0 до 1 с некоторым шагом, находим принадлежащую кривой точку по формуле

$d+v \left(r_m e^{-i t \phi _m}+r_s e^{-i t \phi _s}\right)$

Циркулярные сплайны

Так же, как и кривые Безье, эти кривые можно совмещать для кусочно-непрерывного построения сплайнов. Для обеспечения гладкости в узловых точках (стыковки) необходимо, чтобы узловая точка находилась на одной линии с двумя соседними направляющими точками. Для этого можно задавать узловые точки не явным образом, а через интерполяцию направляющих точек. Их также можно не задавать вообще, вычисляя полностью автоматически например, как среднее между направляющих точек:

Справа для сравнения использован тот же подход с кривыми Безье 2-го порядка.

Замечания и нюансы

В отличие от кривых Безье, здесь кривая не всегда лежит внутри фигуры из линий, соединяющих контрольные точки, например

Кроме того, существует вырожденный случай, который необходимо обрабатывать отдельно когда направляющая точка лежит на одной прямой с узловыми точками. При этом кривая вырождается в прямую, а при попытке вычислить точку d возникает деление на ноль.

У этих кривых также имеется ограничения на кривизну линии, поскольку в соответствии с алгоритмом выбирается наименьший путь следования и кривая не может обогнуть больше, чем 180. Это приводит к тому, что при кусочно-непрерывной интерполяции могут возникать острые углы при определённом положении направляющих точек (справа те же точки для Безье):

Заключение

Дальнейшим развитием рассмотренного метода построения кривых является увеличение количества векторов, участвующих в построении кривой и, соответственно, увеличение количества направляющих точек. Однако, в отличие от кривых Безье, повышение порядка здесь не является очевидным и требует отдельного вдумчивого размышления. Также возможны различные методы комбинации их с кривыми Безье в частности, интерполяции центра окружности рисующих векторов.

Рассмотренный метод построения кривых также не является единственным, частным случаем которого являются дуги окружности и эллипса как минимум, эллипс можно построить через пересечение прямых в параллелограмме (правда, в этом варианте автор потерпел неудачу). Возможно, что существуют и другие решения, в том числе и варианты описанного в статье пишите в комментариях, если вам что-то известно на эту тему.

Исходный код статьи можно скачать на GitHub.

Подробнее..

Категории: Алгоритмы , Математика , Кривые , Интерполяция , Безье , Сплайны , Комплексные числа , Wolfram mathematica

	Русский
	English

Кривые

Равномерное перемещение объекта вдоль кривой

Циркулярные кривые 2-го порядка

Кривые Безье

Циркулярные кривые

Дуга окружности

Дуга эллипса

Дуга гипотрохоиды

Алгоритм

Циркулярные сплайны

Замечания и нюансы

Заключение

Категории

Последние комментарии