Русский
Русский
English
Авторизация
Ip-адрес
Восстановление пароля
Регистрация
Статистика
Реклама

Теория относительности

Недовольное бурчание о задержке сигналов с Марса

20.02.2021 04:23:04 | Автор: admin

В связи со вчерашней посадкой ровера Perseverance на Марс. Хотите почувствовать себя обладателем тайного знания, недоступного простым смертным? Сейчас устроим.

Рецепт простой: берём специальную теорию относительности (СТО), которая описывает механику и кинематику движения при около-световых скоростях и обнаруживаем, что в ней скорость света является инвариантом при переходе от одной инерциальной системы отсчёта к другой. Что это значит? Это значит, что в любой инерциальной системе (то есть такой, которая движется не под ускорением) скорость света одинакова во всех любых других инерциальных системах, даже если они куда-то движутся относительной нашей. И даже не важно с какой скоростью и в какую сторону.

Из этого, кстати, следует один прикольный мозго-выносящий вывод, который мельком упоминается в учебниках и тут же забывается навсегда в инерциальной системе сумма любых досветовых скоростей не может превысить световую. Ибо так завещал великий Хендрик Лоренц, который понатыкал своих коэффициентов в преобразования имени самого себя.

Но мы отвлеклись. Что с ровером? С ним-то всё в порядке, а вот многочисленные восторженные стримы, статьи, заметки и подкасты как с цепи сорвались мол, сейчас сигнал с Марса идёт до Земли 11 с половиной минут, поэтому мы не можем следить за посадкой и управлять ею в режиме реального времени, поэтому там рулит посадкой автоматика с машинным обучением, и вот когда к нам придёт сигнал об успехе, то это значит, что ровер уже сел 11 с половиной минут назад. Ну и всё в таком духе.

И, чёрт побери, даже, на первый взгляд, технически грамотные люди, вроде бы не первый год разбирающиеся в тематике космоса, астрономии, небесной механике и всём прочем, радостно несут эту чушь мощными потоками. Так вот, ответственно заявляю, эта чушь чушь!

Нет никакой задержки на 11 с половиной минут! То есть да сигнал с Марса сейчас идёт именно столько времени, если измерять это время в такой системе, где Земля и Марс более-менее спокойны. Но это не задержка относительно того времени события, о котором мы знаем, что оно наступило по нашим часам, то есть сигнал о котором вышел с Марса в нашу сторону. Почему? Потому, что в СТО одновременность точно так же относительна, как и скорость и точно так же не может превысить скорость света в инерциальной системе!

Если, например, на Землю пришёл сигнал с Марса о посадке ровера ровно в тот момент, как на Земле кто-то чихнул, то эти два события посадка ровера и чих произошли одновременно! А вовсе не с разницей в 11 с половиной минут! Это потому, что сама одновременность летела на Землю вместе с сигналом, распространяясь волнами от эпицентра самого события одновременности.

Заглянем на минутку к астрономам. Там ведь об астрономических событиях вроде взрыва сверхновых или образования чего-нибудь заметного не говорят, что это произошло столько-то миллионов или миллиардов лет назад нет, там считается что это происходит прямо сейчас, вот как наблюдаем, так и происходит. Естественно, отдавая себе отчёт в расстоянии, которое понадобилось преодолеть свету, чтобы мы могли это наблюдать.

Но позвольте, если бы на Земле существовал супер-пупер телескоп, в который бы было оптически видно посадку Perseverance, то сигнал с MRO об успешной посадке пришёл бы на Землю сразу после того, как мы в этот телескоп смогли бы увидеть саму посадку. Сразу после, а не через 11 с половиной минут! Потому, что и оптическому сигналу понадобились бы те же самые 11 с половиной минут, чтобы долететь с Марса до Земли. Тот факт, что это событие было запланировано, ничего не меняет в том, что фронт одновременности не мгновенный, а точно так же летит со скоростью света, как и радио- и оптические сигналы.

Это такой себе mind trick, вызванный тем, что люди привыкли считать свою инерциальную систему отсчёта какой-то более особенной, чем бесконечное множество других, а также тем, что расстояния таких порядков, как сотни миллионов километров тяжело воспринимаются сознанием, привыкшим оперировать более бытовыми величинами.

И, разумеется, всё это не более чем попытка праздно доколупаться, о чём и заголовок статьи. Счастья вам.

Подробнее..
Категории: Астрономия , Научно-популярное , Космонавтика , Марс , Теория относительности , Марсоход

Перевод Черные дыры могут иметь волосы. Эйнштейн не прав?

22.02.2021 16:14:10 | Автор: admin
Недавно проведенное исследование американских физиков об экстремальных черных дырах может опровергнуть знаменитую теорему об отсутствии волос.

Согласно общей теории относительности Эйнштейна, черные дыры обладают только тремя наблюдаемыми свойствами: массой, спином (момент импульса) и зарядом. Дополнительных характеристик, или, как называют их физики, волос, не существует.



Чтобы объяснить идею, представим однояйцевых близнецов. Они имеют одинаковый генотип, это генетические копии, но даже такие близнецы будут различаться множеством вещей: от темперамента до прически. Черные дыры, согласно теории гравитации Альберта Эйнштейна, могут иметь всего три характеристики: массу, спин и заряд. Если эти значения одинаковы для любых двух черных дыр, то они идентичны, будет невозможно отличить одну от другой. У черных дыр нет волос.

Согласно классической общей теории относительности, такие черные дыры были бы абсолютно идентичны, отмечает Пол Чеслер, физик-теоретик из Гарвардского университета.

Однако ученые задаются вопросом, верна ли теорема об отсутствии волос. В 2012 году математик Стефанос Аретакис, работавший тогда в Кембриджском университете, а теперь в Университете Торонто, предположил, что некоторые черные дыры могут иметь нестабильности (instabilities) на горизонте событий.

Нестабильности придали бы одним участкам горизонта черной дыры более сильное гравитационное притяжение, чем другим. Получается, что в таком случае даже идентичные черные дыры будут различимыми.

Однако уравнения Аретакиса показали, что это возможно только для так называемых экстремальных черных дыр тех, которые имеют максимально возможное значение для массы, спина или заряда. И, по словам Чеслера, такие черные дыры не могут существовать в природе.

Но допустим, что есть почти экстремальная черная дыра, которая приближается к максимальным значениям, но не достигает их. Такая черная дыра может существовать, по крайней мере, теоретически. Опровергнет ли это теорему об отсутствии волос?

В докладе, опубликованном в конце января, показано, что это возможно.

Более того, земные детекторы гравитационных волн могут уловить такие волосы.

Аретакис предположил, что существует некоторая информация, которая остается на горизонте событий, прокомментировал Гаурав Ханна, физик из Массачусетского университета и Университета Род-Айленда, один из соавторов исследования.

Ученые предполагают, что свидетельства образования черной дыры или более поздних возмущений горизонта событий (например, падение вещества в черную дыру) могут создавать гравитационную нестабильность на горизонте событий почти экстремальной черной дыры или рядом с ним.

Мы предполагаем, что гравитационный сигнал, который мы обнаружим, будет сильно отличаться от обычных черных дыр, которые не являются экстремальными, говорит Ханна.

Если у черных дыр есть волосы, значит сохраняется некоторая информация об их прошлом, это затронет и знаменитый информационный парадокс черных дыр, который сформулирован Стивеном Хокингом, как отмечает Лия Медейрос, астрофизик из Института перспективных исследований в Принстоне.

Этот парадокс обнажает фундаментальный конфликт между общей теорией относительности и квантовой механикой, двумя столпами физики XX века.

Если опровергнем одно из условий информационного парадокса, мы сможем решить сам парадокс. Одно из условий это теорема об отсутствии волос.

Последствия этого открытия будут значительным. Если мы сможем доказать, что реальное пространство-время черной дыры за пределами черной дыры отличается от того, что мы ожидаем увидеть, тогда, я думаю, это будет иметь действительно огромное значение для общей теории относительности, сказала Медейрос, соавтор октябрьского доклада, который посвящен тому, соответствует ли наблюдаемая геометрия черных дыр предположениям.

Однако, пожалуй, самым захватывающим моментом исследования является то, что оно открывает путь, как объединить наблюдения за черными дырами и фундаментальную физику. Обнаружение волос на черных дырах, пожалуй, на самых экстремальных астрофизических лабораториях во Вселенной, может позволить исследовать такие идеи, как теория струн и квантовая гравитация, таким способом, каким раньше это было невозможно.

Оказывается, уравнения Эйнштейна настолько сложны, что мы ежегодно открываем новые их свойства.

Пол Чеслер

Одна из больших проблем с теорией струн и квантовой гравитацией заключается в том, что эти предположения сложно проверить, утверждает Медейрос, так что, если у нас есть что-то, что можно проверить даже удаленно, это просто потрясающе.

Однако встречаются и серьезные препятствия. Нет уверенности в существовании почти экстремальных черных дыр. По словам Чеслера, в лучших моделях на данный момент обычно образуются черные дыры, которые на 30% отличаются от экстремальных значений. И даже если почти экстремальные дыры существуют, не совсем понятно, достаточно ли чувствительны детекторы гравитационных волн для определения нестабильности по волосам.

Более того, предполагается, что волосы крайне скоротечны, они длятся доли секунды.

Но сам доклад выглядит основательным. Я не думаю, что кто-то в сообществе сомневается в этом, сказал Чеслер.

Следующий этап посмотреть, какие сигналы мы будем обнаруживать с помощью детекторов гравитационных волн: сейчас мы работаем с LIGO и Virgo, но запускается новые инструменты, например, LISA, совместный эксперимент Европейского космического агентства и НАСА по исследованию гравитационных волн.

Теперь следует опираться на их работу и действительно вычислить, какой будет частота гравитационного излучения. Важно понять, как мы можем измерить и идентифицировать его, отмечает Хельви Витек, астрофизик из Университета Иллинойса, Урбана-Шампейн.

Хотя шансы на обнаружить волосы не так велики, такое открытие поставит под сомнение общую теорию относительности Эйнштейна и докажет существование почти экстремальных черных дыр.

Мы хотели бы знать, позволяет ли природа существовать такому зверю, говорит Ханна.
Подробнее..
Категории: Астрономия , Научно-популярное , Чёрные дыры , Эйнштейн , Блог компании timeweb , Timeweb , Теория относительности

Увидеть своими глазами вселенная и Большой взрыв

06.09.2020 10:13:38 | Автор: admin

Метаматериалы композиты со структурными элементами, размерами много меньше длины волны излучения, обладают не только необычными свойствами, такими как отрицательный коэффициент преломления, но и способностью имитировать космологические уравнения. Они открывают новые возможности старым добрым аналоговым компьютерам. А чем хороши аналоговые вычисления? Результат виден практически сразу. Итак, на картинке ниже мы видим Большой взрыв! Читаем, как это получилось.


Большой взрыв и путешествия во времени


image
В своём исследовании, Игорь Смолянинов и Юй-Юу Хунг из Университета Мэриленда построили метаматериал путем нанесения на золотую подложку полосок оргстекла. Математическое описание поведения электромагнитных волн в метаматериале имеет много общего с общей теорией относительности (далее ОТО), которая описывает пространство-время. Следовательно, путь распространения света в метаматериале аналогичен пути массивной частицы в (2+1)-размерном пространстве-времени.


В немагнитном анизотропном материале с диэлектрическими константами $\epsilon_x=\epsilon_y=\epsilon_1$ и $\epsilon_z=\epsilon_2$ волна с компонентой $E_z=\phi$ согласно уравнениям Максвелла:


$ -\frac{\omega^2}{c^2}\phi = \frac{\partial^2\phi}{\epsilon_1\partial z^2}+\frac{1}{\epsilon_2}\left(\frac{\partial^2 \phi}{\partial x^2}+\frac{\partial^2 \phi}{\partial y^2}\right) $


У метаматериала с $\epsilon_1>0$ и $\epsilon_2<0$ это уравнение можно переписать в форме уравнения Клейна-Гордона:


$ -\frac{\partial^2\phi}{\epsilon_1\partial z^2}+\frac{1}{|\epsilon_2|}\left(\frac{\partial^2 \phi}{\partial x^2}+\frac{\partial^2 \phi}{\partial y^2}\right)=\frac{\omega^2}{c^2}\phi=\frac{m^2 c^2}{\hbar^2}\phi $


для массивного скалярного поля. Тогда координата $z$ в уравнении Максвелла подобна времени $t$ в уравнении Клейна-Гордона. При освещении метаматериала лазером, появляющийся световой узор представляет собой историю (2+1)-мерного пространства-времени, населённого частицами с массой $m$. Этот узор составлен из мировых линий частиц, живущих в двумерном пространстве $x,y$ и временем $z$.


Расположение полосок концентрическими окружностями, а не параллельными полосками, приводит к уравнению в цилиндрических координатах:


$ -\frac{\partial^2\phi}{\epsilon_\theta\partial r^2}+\frac{1}{|\epsilon_r|}\left(\frac{\partial^2 \phi}{\partial z^2}+\frac{\partial^2 \phi}{r^2\partial \theta^2}\right)=\frac{\omega^2}{c^2}\phi==\frac{m^2 c^2}{\hbar^2}\phi $


Роль времени теперь играет координата $r$, а условие $\epsilon_\theta > 0$ и $\epsilon_r<0$ реализует аналоговую модель расширяющейся вселенной. Точка $r=0$ соответствует моменту Большого взрыва. Действительно, судя по полученной световой картинке, мировые линии частиц в самом деле расходятся в пространстве с течением времени (по мере удаления от $r=0$).


В статье Смолянинова и Хунг также разбирается вопрос о существовании замкнутых времениподобных кривых. Существование замкнутых времениподобных кривых позволяет путешествия во времени со всеми связанными с ними парадоксами. На метаматериале они бы проявились как световые петли это достаточно очевидно. Однако, в силу разных причин их реализовать не удалось, и, как заключают авторы, скорее всего не удастся. Увы.


Общая теория относительности для инженеров-электриков


Аналогия между электромагнитными полями в метаматериалах и космологией работает в обе стороны. В самом деле, для дизайна метаматериала выполняющего функцию, например, "шапки-невидимки", нужно использовать аппарат общей теории относительности (ОТО). Суть уравнений Эйнштейна ОТО можно сформулировать таким образом: пространство-время указывает материи как ей двигаться, а материя указывает пространству-времени как ему искривляться. Решить уравнение Эйнштейна значит найти вид метрического тензора пространства-времени, т.е. определить его кривизну исходя из распределения материи.

Шапка-невидимка, скрывающая помещенный внутрь объект, должна так искривлять/преломлять лучи света, чтобы они обходили объект. Искривление световых лучей эквивалентно искривлению пространства-времени, а распределение материи эквивалентно распределению диэлектрической проницаемости (и связанному с ней индексу преломления) в метаматериале. Подробнее с примерами взаимосвязь ОТО и разработки метаматериалов разобрана в статье Ульфа Леонхардта и Томаса Филбина General relativity in electrical engineering.


Также по этой теме:


  1. Novello M., Visser M., Volovik G. E. Artificial black holes. World Scientific, 2002. (особенно глава 3: Slow light)
  2. Ralf Schutzhold. Recreating Fundamental Effects in the Laboratory?
Подробнее..
Категории: Научно-популярное , Физика , Теория относительности , Метаматериалы , Моделирование физических процессов

Геометрическое представление кривизны пространства в метрике Шварцшильда

25.09.2020 14:16:06 | Автор: admin
или два плюс два равно четыре.

Для понимания статьи достаточно школьного курса математики.

Форма множителя в метрике Шварцшильда давно не давала мне покоя своей изысканной двуличностью, и я решил уделить некоторое время изысканиям возможностей её преобразования. Сама метрика Шварцшильда получается в результате решения ОТО для вакуумного случая (тензор энергии-импульса равен нулю):

$ds^2 = - \left(1- 2 \frac{GM}{c^2 r}\right) c^2 dt^2 + \left(1- 2 \frac{GM}{c^2 r}\right)^{-1} dr^2 + r^2 \cdot d\theta^2 + r^2 \cdot \sin^2\theta \cdot d\phi^2$


Она описывает пространственно-временной континуум в окрестностях произвольного компактного массивного объекта. Компактного, значит, девиации формы незначительны в отношении к массе. Проще говоря, круглый и плотный. Обычно здесь приводят в пример чёрную дыру. Никто почему-то не приводит примеров некомпактных объектов. Герметичная палка из пенопласта в открытом космосе на бесконечном удалении от массивных объектов, например, некомпактный объект. Кубический конь на расстоянии, с которого можно разглядеть печаль в его глазах тоже.

Через объём 3-сферы


Произведём замену:

$M=\frac{E}{c^2}$


Тогда метрика станет такой:

$$display$$ds^2 = - \left(1- 2 \frac{GE}{c^\color{red}{4} r}\right) c^2 dt^2 + \left(1- 2 \frac{GE}{c^\color{red}{4} r}\right)^{-1} dr^2 + r^2 \cdot d\theta^2 + r^2 \cdot \sin^2\theta \cdot d\phi^2$$display$$


Замена была нужна только для того, чтобы обратить внимание на четвёртую степень у скорости света, потому что все циферки в формулах имеют значение. Об этом говорит вся история физики любая эмпирически полученная формула со временем получает теоретическое основание, объясняющее значения всех математических форм, которые в ней содеражатся.
Обычно в представлении этой метрики часть, связанную с физическими константами и массой тела, создающего поле, выражают через радиус Шварцшильда:

$r_s = 2 \cdot \frac{GE}{c^4}$


потому что метрика имеет особенность в этой точке. Здесь время, буквально, останавливается.
Вот так, в таком случае, выглядит вся метрика:

$ds^2 = - \left(1- \frac{r_s}{ r}\right) c^2 dt^2 + \left(1- \frac{r_s}{r}\right)^{-1} dr^2 + r^2 \cdot d\theta^2 + r^2 \cdot \sin^2\theta \cdot d\phi^2$


Но в продолжение рассуждений о физической сути явлений эта двойка:

$r_s = \color{red}{2} \cdot \frac{GE}{c^4}$


тоже должна быть осмыслена. Поэтому представим так:

$u = \frac{GE}{c^4}$


Это просто половина гравитационного радиуса $r_s$, и размерность у него такая же. Получим:

$ 1 - 2\frac{GE}{c^4r} = 1 - 2\frac{u}{r} $


Напрашивается:

$= \left( 1 - 2\frac{u}{r} + \frac{u^2}{r^2} \right) - \frac{u^2}{r^2} = \left( 1 - \frac{u}{r} \right)^2 - \frac{u^2}{r^2} = \left( \frac{r - u}{r} \right)^2 - \frac{u^2}{r^2} = $


$= \frac{(r-u)^2 - u^2}{r^2} \qquad \qquad (1)$


Уже неплохо. Зарисуем. Представим $r = OB$ конечным отрезком, $u = OA$ его частью, как показано на рисунке ниже. Очевидно, что $(r-u) = AB$.
image
Любопытно, кстати, что из $r_s = 2u$ следует, что точка $A$ находится за (под) горизонтом событий объекта энергии $E$. Вот так легко она находится, а мы не можем.
Теперь покажем, что отношение вида $(1)$ будет выполняться для всех точек, имеющих геометрическое место на перпендикуляре к $OB$ в точке $A$:

$\frac{(r-u)^2 - u^2}{r^2} = \frac{((r-u)^2 + a^2) - (u^2 + a^2)}{r^2} = \frac{b^2 - d^2}{r^2} \qquad \qquad (2) $


image
для любых $b = CB$ и $d = OC$.
Говоря проще, разность квадратов $(r-u)^2 - u^2$ эквивалентна разности любых величин, проекциями которых на $OB$ являются $AB$ и $OA$ соответственно, при условии, что точка $C$ у них общая.
Дальше предположим, что $u = u(E)$ и $(r-u)$, наоборот, проекции $r = OB$ на какие-то оси, то есть пифагорова сумма двух величин, в исходном виде перпендикулярных друг другу. Переводя это в требование, рассмотрим случай $\angle{OCB} = \pi/2$, для которого верно:

$b^2 = r^2 - d^2 \rightarrow (2) \rightarrow \frac{b^2 - d^2}{r^2} = 1 - 2\frac{d^2}{r^2} \qquad \qquad (3)$


image
Доработаем $(3)$ аналогично начальной итерации:

$1 - 2\frac{d^2}{r^2} = \left( 1 - 2\frac{d^2}{r^2} + \frac{d^4}{r^4} \right) - \frac{d^4}{r^4} = \frac{(r^2-d^2)^2 - d^4}{r^4} =$


$= \frac{b^4 - d^4}{\sqrt{b^2 + d^2}^4} = \frac{b^4 - d^4}{r^4}\qquad \qquad (4)$


Вот и четвёртая степень. Формула объёма 3-сферы:

$V = \frac{\pi^2 \cdot R^4}{2}$


Это я к тому, что если домножить и разделить $(4)$ на $\pi^2/2$:

$\frac{b^4 - d^4}{r^4} = \frac{\pi^2}{2} \cdot \frac{2}{\pi^2} \cdot \frac{b^4 - d^4}{r^4} = \frac{V_b - V_d}{V_r} \qquad \qquad (5)$


то множитель в метрике Шварцшильда превращается в разность объёмов двух 3-сфер, построенных вокруг двух радиальных проекций точки относительно центра поля, соотнесённой к объёму 3-сферы, образуемой полным расстоянием между точкой и центром поля.
С учётом того, что полный радиус задаётся проекциями, всю эту конструкцию весьма лаконично задают два параметра, один из которых связан с энергией, а второй нет. Там точно две координаты.

Выводы


Замечательными следствиями такого представления являются:
1. Из формы множителя видно, что поведение фотона ограничивает видимую зону пятимерного пространства-времени. За её пределами можно спрятать нечто гравитирующее, но невидимое.
2. Наличие второй спрятанной координаты избавляет от парадокса нулевого времени.
3. Раз кривизна пространства вокруг массивного тела может быть всегда разложена на две компоненты, одна из которых связана с энергией тела, а вторая исключительно с пространством, то следующим шагом надо решить уравнения ОТО для вакуумного случая пятимерного пространства-времени. Об этом в следующей статье.

Бонус. Через угол


Очевидно, что можно выразить значимость поля в точке через плоский угол, выражающий отклонение траектории движения от плоского пространства (в отсутствие гравитационных полей).
Выразим величины $b$ и $d$ через угол $\alpha = \angle{OBC}$: $b = r \cdot \cos\alpha; \ d = r \cdot \sin\alpha$. Назовём его угол кривизны траектории. Тогда множитель можно выразить очень по-разному:

$1 - 2\frac{GE}{c^4r} = \cos^2\alpha - \sin^2\alpha = \cos^4\alpha - \sin^4\alpha = 1 - 2 \sin^2\alpha = $


$= \frac{1-\tan^2\alpha}{1 + \tan^2\alpha} = \cos2\alpha \qquad \qquad (6) $


Особенно мне нравится вариант с тангенсами.
image
Подставим в исходный интервал:

$ ds^2 = -\cos 2\alpha \cdot c^2dt^2 + \cos^{-1} 2\alpha \cdot dr^2 + r^2 \cdot d\theta^2 + r^2 \cdot \sin^2\theta \cdot d\phi^2 $


Всё, как и должно, превращается в плоскую метрику Минковского при $\alpha = 0$.
Здесь точно должен быть пятый
Продолжение следует.
Подробнее..
Категории: Научно-популярное , Физика , Математика , Космология , Кривизна , Пространство , Гиперпространство , Общая теория относительности , Эйнштейн , Гравитация , Шварцшильд , Теория относительности , Решение ото

ОТО. Геометрическое представление кривизны пространства в метрике Шварцшильда. Часть 2

23.02.2021 10:12:21 | Автор: admin
или один плюс три снова четыре.

Для понимания статьи необходим школьный курс математики, и, может быть, даже достаточен.

В предыдущей статье мы выяснили, что множитель кривизны пространства в метрике Шварцшильда в каждое мгновение может быть представлен как сумма двух перпендикулярных мер (длин), одна из которых зависит от энергии массивного тела, создающего гравитационное поле, а вторая нет.
В этой статье, я объясню выводы предыдущей статьи, часть которых оказалась неочевидна, а также продолжу развитие идеи распрямления искривлённого четырёхмерного пространства-времени через энергетическую глубину.

Чтобы не скакать по ссылкам, предыдущая статья здесь целиком.
Форма множителя в метрике Шварцшильда давно не давала мне покоя своей изысканной двуличностью, и я решил уделить некоторое время изысканиям возможностей её преобразования. Сама метрика Шварцшильда получается в результате решения ОТО для вакуумного случая (тензор энергии-импульса равен нулю):

$ds^2 = - \left(1- 2 \frac{GM}{c^2 r}\right) \cdot c^2 dt^2 + \left(1- 2 \frac{GM}{c^2 r}\right)^{-1} \cdot dr^2 + r^2 \cdot d\theta^2 + r^2 \cdot \sin^2\theta \cdot d\phi^2$


Она описывает пространственно-временной континуум в окрестностях произвольного компактного массивного объекта. Компактного, значит, девиации формы незначительны в отношении к массе. Проще говоря, круглый и плотный. Обычно здесь приводят в пример чёрную дыру. Никто почему-то не приводит примеров некомпактных объектов. Герметичная палка из пенопласта в открытом космосе на бесконечном удалении от массивных объектов, например, некомпактный объект. Кубический конь на расстоянии, с которого можно разглядеть печаль в его глазах тоже.

Через объём 3-сферы


Произведём замену:

$M=\frac{E}{c^2}$


Тогда метрика станет такой:

$$display$$ds^2 = - \left(1- 2 \frac{GE}{c^\color{red}{4} r}\right) c^2 dt^2 + \left(1- 2 \frac{GE}{c^\color{red}{4} r}\right)^{-1} dr^2 + r^2 \cdot d\theta^2 + r^2 \cdot \sin^2\theta \cdot d\phi^2$$display$$


Замена была нужна только для того, чтобы обратить внимание на четвёртую степень у скорости света, потому что все циферки в формулах имеют значение. Об этом говорит вся история физики любая эмпирически полученная формула со временем получает теоретическое основание, объясняющее значения всех математических форм, которые в ней содеражатся.
Обычно в представлении этой метрики часть, связанную с физическими константами и массой тела, создающего поле, выражают через радиус Шварцшильда:

$r_s = 2 \cdot \frac{GE}{c^4}$


потому что метрика имеет особенность в этой точке. Здесь время, буквально, останавливается.
Вот так, в таком случае, выглядит вся метрика:

$ds^2 = - \left(1- \frac{r_s}{ r}\right) c^2 dt^2 + \left(1- \frac{r_s}{r}\right)^{-1} dr^2 + r^2 \cdot d\theta^2 + r^2 \cdot \sin^2\theta \cdot d\phi^2$


Но в продолжение рассуждений о физической сути явлений эта двойка:

$r_s = \color{red}{2} \cdot \frac{GE}{c^4}$


тоже должна быть осмыслена. Поэтому представим так:

$u = \frac{GE}{c^4}$


Это просто половина гравитационного радиуса $r_s$, и размерность у него такая же. Получим:

$ 1 - 2\frac{GE}{c^4r} = 1 - 2\frac{u}{r} $


Напрашивается:

$= \left( 1 - 2\frac{u}{r} + \frac{u^2}{r^2} \right) - \frac{u^2}{r^2} = \left( 1 - \frac{u}{r} \right)^2 - \frac{u^2}{r^2} = \left( \frac{r - u}{r} \right)^2 - \frac{u^2}{r^2} = $


$= \frac{(r-u)^2 - u^2}{r^2} \qquad \qquad (1)$


Уже неплохо. Зарисуем. Представим $r = OB$ конечным отрезком, $u = OA$ его частью, как показано на рисунке ниже. Очевидно, что $(r-u) = AB$.
image
Любопытно, кстати, что из $r_s = 2u$ следует, что точка $A$ находится за (под) горизонтом событий объекта энергии $E$. Вот так легко она находится, а мы не можем.
Теперь покажем, что отношение вида $(1)$ будет выполняться для всех точек, имеющих геометрическое место на перпендикуляре к $OB$ в точке $A$:

$\frac{(r-u)^2 - u^2}{r^2} = \frac{((r-u)^2 + a^2) - (u^2 + a^2)}{r^2} = \frac{b^2 - d^2}{r^2} \qquad \qquad (2) $


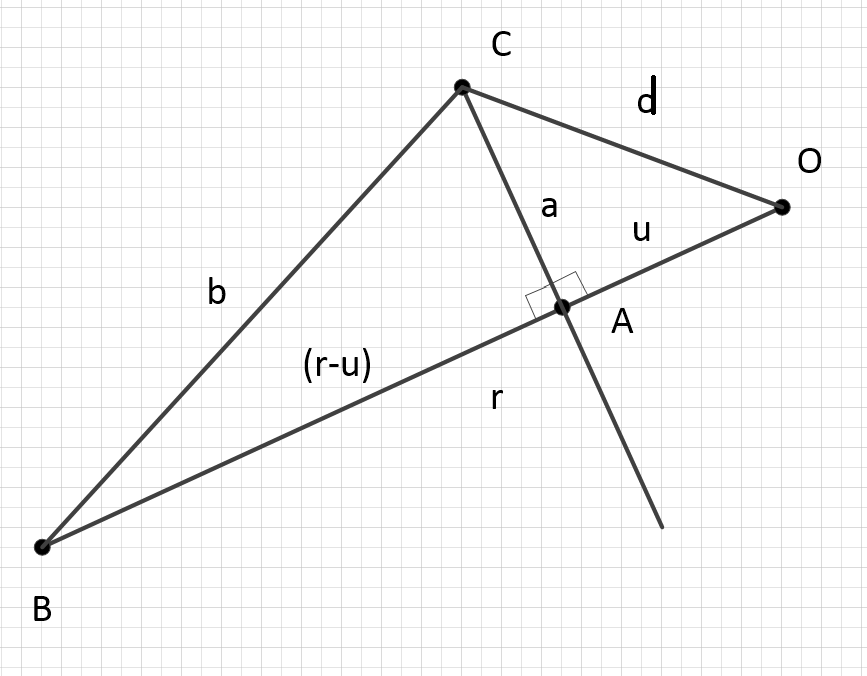
image
для любых $b = CB$ и $d = OC$.
Говоря проще, разность квадратов $(r-u)^2 - u^2$ эквивалентна разности любых величин, проекциями которых на $OB$ являются $AB$ и $OA$ соответственно, при условии, что точка $C$ у них общая.
Дальше предположим, что $u = u(E)$ и $(r-u)$, наоборот, проекции $r = OB$ на какие-то оси, то есть пифагорова сумма двух величин, в исходном виде перпендикулярных друг другу. Переводя это в требование, рассмотрим случай $\angle{OCB} = \pi/2$, для которого верно:

$b^2 = r^2 - d^2 \rightarrow (2) \rightarrow \frac{b^2 - d^2}{r^2} = 1 - 2\frac{d^2}{r^2} \qquad \qquad (3)$


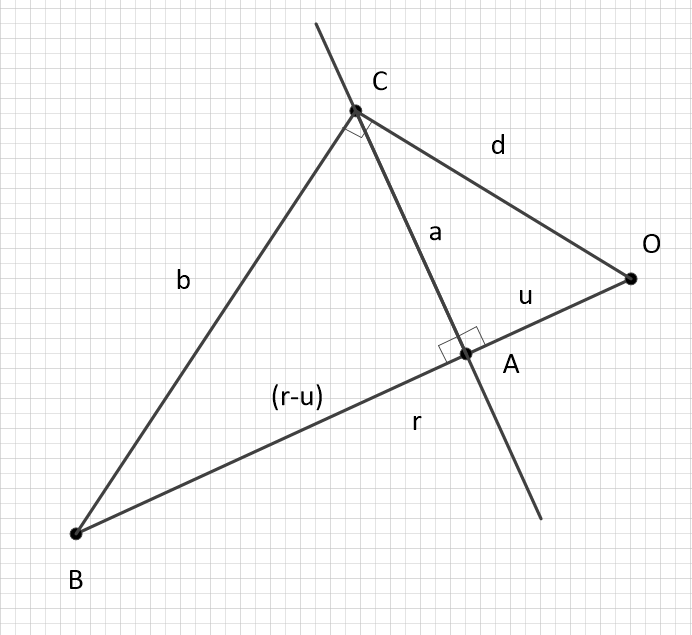
image
Доработаем $(3)$ аналогично начальной итерации:

$1 - 2\frac{d^2}{r^2} = \left( 1 - 2\frac{d^2}{r^2} + \frac{d^4}{r^4} \right) - \frac{d^4}{r^4} = \frac{(r^2-d^2)^2 - d^4}{r^4} =$


$= \frac{b^4 - d^4}{\sqrt{b^2 + d^2}^4} = \frac{b^4 - d^4}{r^4}\qquad \qquad (4)$


Вот и четвёртая степень. Формула объёма 3-сферы:

$V = \frac{\pi^2 \cdot R^4}{2}$


Это я к тому, что если домножить и разделить $(4)$ на $\pi^2/2$:

$\frac{b^4 - d^4}{r^4} = \frac{\pi^2}{2} \cdot \frac{2}{\pi^2} \cdot \frac{b^4 - d^4}{r^4} = \frac{V_b - V_d}{V_r} \qquad \qquad (5)$


то множитель в метрике Шварцшильда превращается в разность объёмов двух 3-сфер, построенных вокруг двух радиальных проекций точки относительно центра поля, соотнесённой к объёму 3-сферы, образуемой полным расстоянием между точкой и центром поля.
С учётом того, что полный радиус задаётся проекциями, всю эту конструкцию весьма лаконично задают два параметра, один из которых связан с энергией, а второй нет. Там точно две координаты.

Через угол


Очевидно, что можно выразить значимость поля в точке через плоский угол, выражающий отклонение траектории движения от плоского пространства (в отсутствие гравитационных полей).
Выразим величины $b$ и $d$ через угол $\alpha = \angle{OBC}$: $b = r \cdot \cos\alpha; \ d = r \cdot \sin\alpha$. Назовём его угол кривизны траектории. Тогда множитель можно выразить очень по-разному:

$1 - 2\frac{GE}{c^4r} = \cos^2\alpha - \sin^2\alpha = \cos^4\alpha - \sin^4\alpha = 1 - 2 \sin^2\alpha = $


$= \frac{1-\tan^2\alpha}{1 + \tan^2\alpha} = \cos2\alpha \qquad \qquad (6) $


Особенно мне нравится вариант с тангенсами.
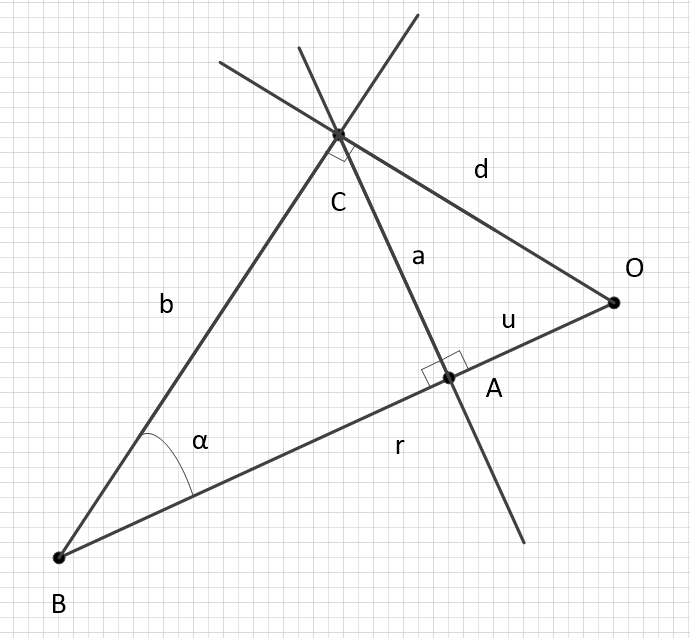
image
Подставим в исходный интервал:

$ ds^2 = -\cos 2\alpha \cdot c^2dt^2 + \cos^{-1} 2\alpha \cdot dr^2 + r^2 \cdot d\theta^2 + r^2 \cdot \sin^2\theta \cdot d\phi^2 $


Всё, как и должно, превращается в плоскую метрику Минковского при $\alpha = 0$.
Здесь точно должен быть пятый
Продолжение следует.

Если коротко, то мы представляем метрику Шварцшильда:

$ds^2 = - \left(1- 2 \frac{GM}{c^2 r}\right) \cdot c^2 dt^2 + \left(1- 2 \frac{GM}{c^2 r}\right)^{-1} \cdot dr^2 + r^2 \cdot d\theta^2 + r^2 \cdot \sin^2\theta \cdot d\phi^2$


где $M$ масса тела, $s$ интервал, $t$ время, $r, \theta, \phi$ сферические координаты, $G, c$ вселенские константы, так:

$ ds^2 = - \frac{V_b - V_d}{V_r} \cdot c^2 dt^2 + \frac{V_r}{V_b - V_d} \cdot dr^2 + r^2 \cdot d\theta^2 + r^2 \cdot \sin^2\theta \cdot d\phi^2 \qquad (1) $


где $V_b, V_d, V_r - $ объёмы 3-сфер, заданных радиусами: $b$ в псевдоевклидовом пространстве, энергорадиусом $d$ массы гравитирующего тела и их суммой $r = \sqrt{b^2 + d^2}$;
и так:

$ ds^2 = -\cos 2\alpha \cdot c^2dt^2 + \cos^{-1} 2\alpha \cdot dr^2 + r^2 \cdot d\theta^2 + r^2 \cdot \sin^2\theta \cdot d\phi^2 \qquad (2) $


где $\alpha$ угол кривизны угол отклонения траектории объекта от нормальной (от её проекции на плоское трёхмерное пространство).
Физически интерпретировать смысл формулы $(1)$ можно было бы так: объект, движущийся в бесконечном вечном асимптотически плоском пространстве Шварцшильда, приближаясь к массивному объекту, будет испытывать дефицит пространства в направлении центра масс гравтела, словно там из ткани космоса вынули часть 4-объёма, пропорциональную массе гравтела и обратно пропорциональную расстоянию до его центра масс. Важным аспектом при этом является то, что изменение кривизны происходит линейно изменению четырёхмерного объёма 3-сферы, а не трёхмерного, потому оно и выглядит таким одутловатым в стандартной метрике.
Это достаточно образная трактовка, которая возможно поможет взглянуть на метрику другими глазами. А формулу $(2)$ я пока трактовать не буду, потому что по ходу данной статьи она ещё получит свою интерпретацию.
Далее я сперва объясню выводы предыдущей статьи, а затем перейду к развитию темы с представлением метрики через дополнительное измерение.

Часть 1. Выводы предыдущей статьи и пояснения к ним



Выводы предыдущей статьи с пояснениями

Выводы


Из возможности такого представления были сделаны следующие выводы:
1. Из формы множителя видно, что поведение фотона ограничивает видимую зону пятимерного пространства-времени. За её пределами можно спрятать нечто гравитирующее, но невидимое.
2. Наличие второй спрятанной координаты избавляет от парадокса нулевого времени.
3. Раз кривизна пространства вокруг массивного тела может быть всегда разложена на две компоненты, одна из которых связана с энергией тела, а вторая исключительно с пространством, то следующим шагом надо решить уравнения ОТО для вакуумного случая пятимерного пространства-времени.

Ограничение видимой зоны пятимерного пространства


Чтобы наглядно объяснить первый вывод предыдущей статьи, представим множитель кривизны траектории объекта так:
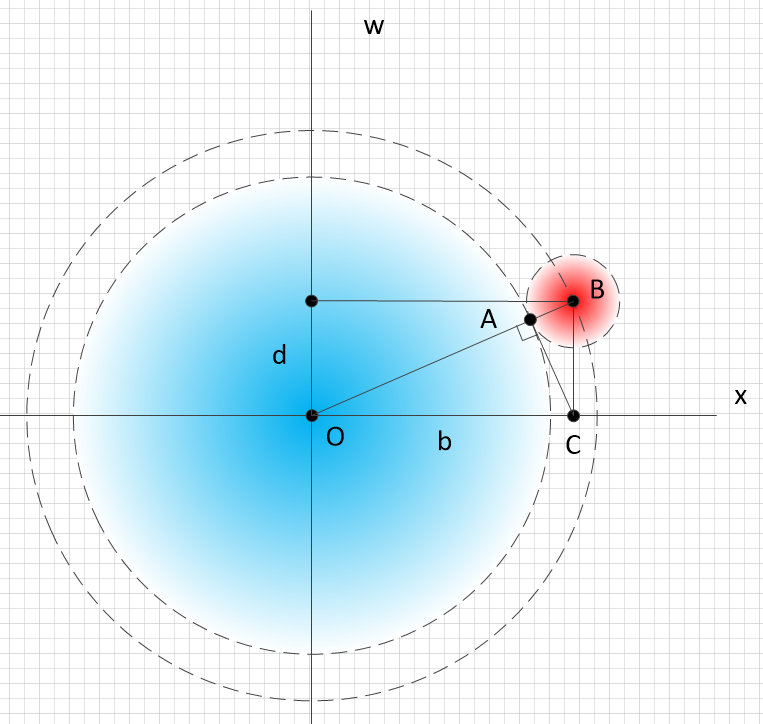
image
где $OB$ полное расстояние $r$ до массивного объекта, $b$ величина координаты, не связанной с энергией массивного тела, $d$ величина координаты, связанной с энергией массивного тела, энергетическая глубина.
Единственное отличие от представления в предыдущей статье в том, что для наглядности картинка перевёрнута: переставлены местами величины $ u = AB $ и $ (r-u) = OA $, то есть энергетическая глубина как бы отнесена к движущейся точке, вместо самого объекта. На итоговый результат это не влияет, но позволяет наглядно представить множитель $ \cos 2\alpha = \cos^2\alpha - \sin^2\alpha $, потому что обратные проекции $b$ и $d$ на гипотенузу $r = OB$ являются квадратами косинуса и синуса угла $\angle BOC = \alpha$ соответственно. Иначе говоря:

$ \cos 2\alpha = \cos^2 \alpha - \sin^2 \alpha = \frac{OA^2 - AB^2}{OB^2} $


Таким образом, кривизна движения объекта, находящегося в точке $B$ относительно массивного объекта в точке $O$ определяется как отношение разности площадей кругов радиусов $OA$ (синего) и $AB$ (красного) в отношении к кругу радиуса $r = OB$.
Движение по осям рекурсивно влияет на обе координаты измерения неразрывно связаны, и в зависимости от показателя массы движущегося объекта траектория кривой будет изменяться, принимая крайнее положение при $ m=0, \ ds^2 = 0 $, то есть для фотона. При этом область возможных траекторий движущихся объектов, обладающих массой, будет находится с одной стороны от траектории фотона $ (ds^2 > 0) $ (в стандартном представлении интервала, для $(2)$ наоборот $ (ds^2 < 0) $ ), будучи ею предельно ограничена.
Таким образом, в обстоятельствах описываемых интервалом, заданным через угол кривизны, пространство всегда можно условно разделить на две области: дофотонную внутреннюю (ниже обозначена красным: при той же кривизне проходимые расстояния меньше, чем у света), и постфотонную внешнюю (ниже синим).
image
Из изложенного логически вытекает отрицательность интервала $( ds^2 < 0 )$ привычного вида для объектов в синей части, и как следствие его пространственно-подобность. Однако, это следствие ограниченной применимости интервала четырёхмерного пространства-времени для описания континуума большей размерности.
Если мысленно увязать ось $ w $ с явлением энергии, то синюю область можно попробовать трактовать как часть плоского пространства, которая однако вследствие гравитации имеет такую энергетическую плотность, что электромагнитные волны её обтекают, и делают тем самым ненаблюдаемой.
Совсем утрировано: все объекты с более кривыми траекториями, чем у света, будут видимы, а менее кривые нет. При этом для того, чтобы оказаться скрытыми, им совершенно необязательно двигаться быстрее света проходить большее пространство за то же время находится правее прямой, соответствующей $ ds^2 = 0 $ в точке. Им достаточно находится ниже этой прямой, и они останутся скрыты гравитационным искривлением, взаимодействуя с гравитирующим объектом легче, чем свет.
Завершу эту главу фантазией, предположив, что в тёмное пространство под синим подолом гравитационного поля можно было бы спрятать, например, пару гораздо более энергоёмких поколений частиц (II и III), таких неустойчивых в нашем 4-континууме.
Если большое количество такого рода частиц разместить компактно, то такое скопление при наблюдении проявляло бы свойства тёмной материи само создавало гравитационное поле, оставаясь при этом вне фотонного пространства невидимым.
Естественно, это всего лишь недоказанные наброски большими мазками. Догадки, которые должны быть высказаны уже только затем, чтобы выявить противоречивость подхода в целом на раннем этапе. А также, вопреки своей возможной ложности в деталях, они могут, наоборот, подстегнуть чей-то интерес к подходу.

Ненулевое время в особенной точке метрики


Здесь предлагаю для начала взглянуть на изменение угла кривизны в динамике:
image
Если условно представить движение объекта в гравитационном поле поворотом относительно плоского трёхмерного пространства наблюдателя, то исходное количество движения останется прежним, изменится только его конфигурация.
Я хочу сказать, что гравитационное поле можно представить пожирателем движения фундаментальных частиц, словно оно является воронкой в никуда, поворачивая их перемещение из наблюдаемого пространства в невидимом направлении, определённо связанном с наблюдаемым нами явлением энергии.
Причём, говоря поворачивая, я, естественно, не подразумеваю поворот в обычном, наблюдаемом пространстве. Гравитационное поле забирает часть движения частиц, как если бы те вращались и могли быть охарактеризованы частотой вращения комплексной составляющей, а гравитационное поле было берегом, который поджимает заходящие на него волны меняет количество движения вдоль, переводя его в движение поперёк. Увеличивает мнимую составляющую, уменьшая вещественную.
Таким образом, в предлагаемой парадигме континуума расширенной мерности движение не исчезает и не растягивается/сжимается. Оно перетекает из плоского наблюдаемого пространства $(x,y,z)$ в перпендикулярном направлении совокупно определённом ранее как единая ось $w$, хоть полноценной осью, изоморфной остальным, судя по всему, не является. Однако ставка на аналогичное представление времени сто лет назад сыграла, хоть ось времени также не совсем обычна, поэтому продолжим пилить в этом месте.
Изменение относительного положения движущегося объекта в пространстве рекурсивно влияет на характеристику его дальнейшего движения так, как если бы на каждый тик $dt^2$ часть движения переходила из наблюдаемого плоского пространства в перпендикулярном ему направлении или наоборот в зависимости от направления.
Соответственно, точка $ r_{s} = 2 GE / c^4 $ (угол кривизны $\alpha = \pi / 4 $) является граничным условием для безмассового объекта, при котором количество наблюдаемого движения объекта становится равно количеству движения изымаемого полем, что реконфигурирует собственное движение объекта в нечто иное, но прекращения движения последнего в пространстве $(w,x,y,z)$ при этом всё же не происходит. Движение остаётся, мы его просто не видим.
Время объекта не останавливается, а энергия количество движения не становится бесконечной.


Решение уравнений ОТО для пятимерного пространства


Вначале я попытался пойти этим путём. С позволения сказать, в штыковую атаку. Но несколько недиагональных компонент в тензоре Риччи получились отличными от нуля (из-за взаимного влияния координат на неизвестные функции), и я не знал, что с этим дальше делать. Насильно приравнять нулю, и получить требуемую форму взаимодействия искомых функций, дало интересный результат, но, кроме этого допущения, логически получалось, что дополнительное измерение, будучи связанным с энергией, имело все шансы оказаться включением правой части уравнений составной частью тензора энергии-импульса (ТЭИ), и тогда его введение в геометрическую левую часть вряд ли сохраняло бы тождества.
В итоге, глядя на косую симметрию в метрике Шварцшильда и на угловую форму мультипликатора в метрике Фридмана, я подумал, а не получилось ли так, что на существующем этапе развития физической теории использование римановой геометрии дало чрезвычайно изящное представление о гравитационном поле в виде ОТО настолько прекрасное, что оно намертво вплело парадигму изгибаемого, неевклидового пространства-времени в умы нескольких поколений физиков. Окажись она ложной не в математическом выражении, но в самой сути представления явлений природы, и стагнация развития теоретической физики, запертой в тензорной ловушке, была бы обеспечена.
Забегая вперёд, выскажу догадку, что если всё-таки развернуть ТЭИ через геометрическое представление тотально, то его можно будет перенести в левую часть, и свернуть с формами пространственного тензора в более развитую, сложную, но в то же время и более лаконичную, форму расширенной мерности.
Однако, чтобы сделать это необходимо попытаться понять суть происходящих процессов называемых явлением гравитации заново. С какой-то другой, неизученной стороны.
Показанный в предыдущей статье принцип демонстрирует возможность ежемгновенного разложения искривления пространства вокруг массивного компактного объекта на ортогональные компоненты, что даёт нам возможность сделать шаг назад, к евклидовой геометрии, и посмотреть с этой позиции на явление гравитации как на поведение объектов внутри евклидова пространства увеличенной размерности, как если бы гравитация была явлением деформирующим сами объекты и их наблюдаемое поведение (относительность времени), а пространство и время при этом оставляла абсолютными (что даёт в перспективе отличный мостик обратно к энергии и её сохранению).
Подход в лоб не сработал, и я пошёл в обход.

Дополнительная ось комплексного пространства


Невидимое окно, в которое вытекает движение, выраженное объёмом $ V_d $ в объёмном представлении кривизны, возникает на горизонте объекта и зовёт в себя провалиться, тем неотвратимее, чем выше его относительная важность (масса к массе) против объекта и расстояние, читай, пространство, которое их разделяет.
Если объект склоняется к этому окну не только в видимом пространстве, но и незримо начинает участвовать в некотором дополнительном движении, по мере приближения соотносясь с мерой внутреннего движения объекта собственной участвуя в потоке, и отдавая на это часть собственного движения из видимого пространства, то из другого среза видимого пространства такой процесс выглядел бы как искривление времени, хотя в самом деле являлся его перераспределением.
Скажу проще. Кусок четырёхмерного объёма $V_d$, чьё возникновение в объёмном представлении кривизны в метрике Шварцшильда:

$ \frac{V_b - V_d}{V_r} = | V_d = 0 | = 1 $


обуславливает её отклонение от псевдоевклидовой метрики, то есть, собственно, и отвечает за возникновение этой самой кривизны континуума, в четырёхмерной (3-пространство и время) версии последнего вырезается на каждый тик $ dt^2 $, и разжиженные остатки пространства-времени стягиваются в центр, склеиваясь краями, чтобы не было видно дыры.
Я же просто предлагаю попробовать дать этой катаракте собственное измерение, чтобы уже перестать натягивать четырёхмерную сову на пятимерный, как минимум, глобус.
В дополнение к трём осям $(\rho, \theta, \phi)$ (для удобства сразу представим его в сферических координатах) введём ось $ w $.
В предыдущей статье мы увидели, что радиальное смещение объекта в гравитационном поле в любой момент времени может быть представлено пифагоровой суммой двух величин:

$ r^2 = b^2 + d^2 $


одна из которых $ b $ не связана с энергией массивного тела (в отсутствие $ d $ оставляет пространство-время плоским), а другая $ d $ связана.
Теперь, чтобы двигаться дальше, представим составляющую $ d $ частью мнимой оси $ w $, а $ b $ частью вещественной оси $ \rho $:

$ r^2 = \rho^2 + \imath^2 w^2 $


где $ \rho $ радиальная координата псевдоевклидова пространства, а $ w $ дополнительная ось энергетического характера.
Как минимум, чтобы не получать $ dd $ при дифференцировании последнего.

Двухмерная радиальная координата


Дальше в комплексном представлении радиальной координаты используется только соответствующая координата плоского пространства $ \rho $. Ось $ \rho $ будет вещественной, её единичным вектором будет $\hat{h}$.
Мнимой осью будет количество требуемого (изымаемого из наблюдаемого пространства) гравитацией движения объекта (как своего рода эвфемизм для $ E = mc^2 $, ведь именно наличие энергии массы создаёт поле) элементарной частицы или их совокупности $ w $. Для обозначения единичного вектора этой оси мы введём несколько необычное для мнимой единицы обозначение $\hat{v} = \sqrt{-1} $, чтобы далее не путать со стандартным набором $ \imath, \jmath, k $ мнимых единиц в кватернионе, с которым столкнёмся в третьей статье цикла.
Тогда состояние поля, создаваемого некоторым массивным объектом, в любой точке расширенного таким образом пространства можно представить как разность квадратов расстояния до центра объекта в плоском 3-пространстве и некоторой энергетической глубины, которую требует поле в виде своего рода контрибуции движения, изымаемого из плоского наблюдаемого пространства, объекта, перемещающегося с наличием радиальной компоненты:

$ \vec{r}^2 = \vec{\rho}^2 + \vec{w}^2 = \hat{h}^2 \cdot \rho^2 + \hat{v}^2 \cdot w^2 $


В представленном таким двухмерным образом пространстве $ ( \rho, w ) $, мы можем описать произвольный вектор $ \vec{r}$ через векторную сумму действительного и мнимого векторов:

$ \vec{r} = \vec{\rho} + \vec{w} = \hat{h} \cdot \rho + \hat{v} \cdot w $


Кроме того, ввиду псевдоевклидовости комплексной плоскости верным будут также:

$ d\vec{r}^2 = \hat{h}^2 \cdot d\rho^2 + \hat{v}^2 \cdot dw^2 = d\rho^2 - dw^2 $


Также нам пригодится такой результат дифференцирования первой формулы в этой главе:

$ \vec{r} \cdot d\vec{r} = \hat{h}^2 \cdot \rho \cdot d\rho + \hat{v}^2 \cdot w \cdot dw $


Эта замечательная форма даст нам далее некоторые удобные инструменты.

Комплексное представление расширенного пространства


Теперь не поленимся, и проверим как изменится выражение множителя метрики Шварцшильда в комплексном представлении:

$\begin{array}{rlcl} ] & \Xi & = & 1- 2 \cdot \frac{GE}{c^4 r}; \\ ] & \vec{u} & = & \frac{GE}{c^4} = e^{z_1} = e^{x_1 + \imath \alpha}, \ \vec{u}, z_1 \in \mathbb{C}; \\ ] & \vec{r} & = & e^{z_2} = e^{x_2 + \imath \alpha} = |r| \cdot e^{\imath \alpha}, \ \vec{r}, z_2 \in \mathbb{C}: \quad \Xi = 1 - 2 \cdot \frac{\vec{u}}{\vec{r}}; \\ & \Xi & = & 1 - 2 \cdot \frac{\vec{u}}{\vec{r}} + \frac{\vec{u}^2}{\vec{r}^2} - \frac{\vec{u}^2}{\vec{r}^2} = \left( \frac{\vec{r} - \vec{u}}{\vec{r}} \right)^2 - \frac{\vec{u}^2}{\vec{r}^2} = \\ & & = & \left( \frac{\vec{r} - \vec{u}}{\vec{r}} \right)^2 + \frac{\vec{a}^2}{\vec{r}^2} - \frac{\vec{u}^2}{\vec{r}^2} - \frac{\vec{a}^2}{\vec{r}^2}, \quad \vec{a} \in \mathbb{C} : \\ ] & \Re(r) & = & ( \vec{r} - \vec{u} ) + \vec{a}; \\ ] & \Im(r) & = & (\vec{u} - \vec{a}) / \imath = - (\vec{u} - \vec{a}) \cdot \imath: \\ & \vec{r} & = & \Re(r) + \Im(r) \cdot \imath \\ \exists & e^{\imath \alpha}, \quad \vec{a} & \perp & \vec{r}: \\ & \Re^2(r) & = & ( \vec{r} - \vec{u} )^2 + \vec{a}^2; \\ & \Im^2(r) & = & - \vec{u}^2 - \vec{a}^2 : \\ & \Xi & = & \frac{\Re^2(r)}{\vec{r}^2} + \frac{\Im^2(r) }{ \vec{r}^2}; \\ ] & \vec{\rho} & = & \Re(r); \\ ] & \vec{w} & = & \Im(r): \\ & \Xi & = & (\vec{\rho}^2 + \vec{w}^2 ) / \vec{r}^2 = \\ & & = & |\vec{r}|^2 / \vec{r}^2 = \\ & & = & e^{-2 \alpha \imath} \end{array}$


Любую пару скалярных чисел $ ( r; u ) $ можно представить парой таких коллинеарных векторов $ ( \vec{r}; \vec{u} ) \in \mathbb{C} $ в комплексной плоскости, что угол поворота (кривизны) $ \alpha = \mathtt{ Arg(\vec{r}) } $ задавал его действительную и мнимую части как обратные проекции векторов $ (\vec{r} - \vec{u}) $ и $ \vec{u} $ на оси, соответственно.
Наглядно (показано в первом квадранте, для четвёртого отрицательного угла $ \alpha $ естественно, тоже работает):
image
Переворот дополнительной оси $ w $ из действительного во мнимое пространство позволил нам выразить радиальную компоненту метрики Шварцшильда гораздо элегантнее:

$ \frac { dr^2 }{ 1 - 2 \cdot \frac{ GE }{ c^4 \cdot r}} = e^{ 2 \alpha \imath } \cdot d\vec{r}^2 \rightarrow (1) $


Это, как минимум, красиво.

Время


Множитель темпоральной компоненты при переносе вектора $ \vec{r} $ на комплексную плоскость перевернулся, но для компоненты в целом это ничего не меняет хоть аргумент стал отрицательным, $ \cos $ чётная функция.

$ \begin{array}{ccl} e^{-2 \hat{v} \alpha } \cdot dt^2 & = & \left[ \hat{h} \cdot \cos (-\alpha) + \hat{v} \cdot \sin (-\alpha) \right]^2 \cdot dt^2 = \\ & = & \left[ \cos^2 \alpha + \hat{ v }^2 \cdot \sin^2 \alpha \right] \cdot dt^2 \end{array} $


Именно это свойство времени подспудно подтолкнуло меня к мысли о его абсолютности как бы взаимно не располагались две другие части расширенной метрики, время объекта в континууме наблюдателя всегда меняется одинаково. Оно тратится на перемещение, в каком бы направлении не происходило движение, и как бы ни выражалось.
Подробнее об этом в третьей статье цикла.

Радиальная компонента


Очевидно, что $ e^{ 2 \alpha \imath } $ часть самого вектора $ \vec{r} = |r| \cdot e^{ \alpha \imath } $, тогда нам остаётся только дополнить её модулем $ |r|^2 $, чтобы сломать окончательно:

$ (1) \rightarrow e^{ 2 \alpha \imath } \cdot d\vec{r}^2 = \frac{ |r|^2 \cdot e^{ 2 \alpha \imath } \cdot d\vec{r}^2 }{ |r|^2 } = \left( \frac{ \vec{r} \cdot d\vec{r} }{ |r| } \right)^2 \rightarrow (2) $


Как было показано выше, $ \vec{r} \cdot d\vec{r} = \hat{h}^2 \cdot \rho \cdot d\rho + \hat{v}^2 \cdot w \cdot dw $, подставим:

$ (2) \rightarrow \left( \frac{ \vec{r} \cdot d\vec{r} }{ |r| } \right)^2 = \left( \frac{ \hat{h}^2 \cdot \rho \cdot d\rho + \hat{v}^2 \cdot w \cdot dw }{ |r| } \right)^2 = \hat{h}^4 \cdot \cos^2 \alpha \cdot d\rho^2 + \hat{v}^4 \cdot \sin^2 \alpha \cdot dw^2 $


И вот энергоглубина, выделенная в отдельную координату $ w $, изящно отвалилась по шву от плоского пространства.

Угловые координаты


Чтобы преобразовать угловые координаты, выразим квадрат вектора $ \vec{r} $ с учётом поворота на угол кривизны:

$ \begin{array}{ccl} \vec{r}^2 & = & \hat{h}^2 \cdot |r|^2 \cdot\cos^2 \alpha + \hat{v}^2 \cdot |r|^2 \cdot \sin^2 \alpha = \\ & = & ( \rho^2 + w^2 ) \cdot (\cos^2 \alpha - \sin^2 \alpha) = \\ & = & \rho^2 \cdot \cos^2 \alpha - w^2 \cdot \sin^2 \alpha - \rho^2 \cdot \sin^2 \alpha + w^2 \cdot \cos^2 \alpha = \\ & = & \rho^2 \cdot \cos^2 \alpha - w^2 \cdot \sin^2 \alpha - \frac{ \rho^2 \cdot w^2 }{ |r|^2 } + \frac{ w^2 \cdot \rho^2 }{ |r|^2 } = \\ & = & \rho^2 \cdot \cos^2 \alpha - w^2 \cdot \sin^2 \alpha = \\ & = & \rho^2 \cdot \cos^2 \alpha + \hat{v}^2 \cdot w^2 \cdot \sin^2 \alpha \end{array} $



Преобразование интервала


Теперь мы можем разделить координаты во всём интервале полностью:

$ \begin{array}{ccl} ds^2 & = & \left( 1 - \frac{ GE }{ \mathtt{ c }^4 r } \right) \cdot dt^2 - \left( 1 - \frac{ GE }{ \mathtt{ c }^4 r } \right)^{-1} \cdot dr^2 - r^2 \cdot d\theta^2 - r^2 \cdot \sin^2 \theta \cdot d\phi^2 = \\ & = & \color{red}{ \cos^2 \alpha \cdot dt^2 - \sin^2 \alpha \cdot dt^2 } - \\ & - & \color{green} { \cos^2 \alpha \cdot d\rho^2 - \cos^2 \alpha \cdot \rho^2 \cdot \left[ d\theta^2 + \sin^2 \theta \cdot d\phi^2 \right] } - \\ & - & \color{blue}{ \sin^2 \alpha \cdot dw^2 + \sin^2 \alpha \cdot w^2 \cdot \left[ d\theta^2 + \sin^2 \theta \cdot d\phi^2 \right] } = \\ & = & \color{red}{ \cos^2 \alpha \cdot dt^2 } - \color{green} { \cos^2 \alpha \cdot \left[ d\rho^2 + \rho^2 \cdot d\theta^2 + \rho^2 \cdot \sin^2 \theta \cdot d\phi^2 \right] } - \\ & - & \color{red}{ \sin^2 \alpha \cdot dt^2 } + \color{blue}{ \sin^2 \alpha \cdot \left[ - dw^2 + w^2 \cdot d\theta^2 + w^2 \cdot \sin^2 \theta \cdot d\phi^2 \right] } = \\ & = & \cos^2 \alpha \cdot \left[ \color{red}{ dt^2 } - \color{green} { d\rho^2 - \rho^2 \cdot d\theta^2 - \rho^2 \cdot \sin^2 \theta \cdot d\phi^2 } \right] - \\ & - & \sin^2\alpha \cdot \left[ \color{red}{ dt^2 } - \color{magenta}{ \hat{?}^2 } \color{blue}{ \cdot dw^2 - w^2 \cdot d\theta^2 - w^2 \cdot \sin^2 \theta \cdot d\phi^2 } \right] \rightarrow ? \\ & \rightarrow & \cos^2 \alpha \cdot \color{green}{ ds_\rho^2 } - \sin^2 \alpha \cdot \color{blue}{ ds_w^2 } \end{array} $


Вот так поворот. Был бы, если бы не перевёрнутый знак перед $ dw^2 $ (маджента). Именно такая возможность представления формы метрики Шварцшильда не давала мне покоя, но почему возникает ошибка?
Как бы по-идиотски это не звучало, она возникает, потому что мы выносим не тот минус один, который, будучи вынесенным, даст положительное значение при $ dw^2 $, а тот, который оставит $ dw^2 $ отрицательным, как и оба других слагаемых угловых координат.
Для того, чтобы разобраться в этой математике, нам потребуется ввести дополнительный вектор $ \hat{ u }^2 = -1, \ \hat{ u } \in \Im $ мнимой оси комплексного пространства, который задаёт 3-пространство относительно времени в стандартном интервале, например, в метрике Минковского:

$ ds^2 = dx_0^2 + \hat{ u }^2 \cdot \left[ dx_1^2 + dx_2^2 + dx_3^2 \right] $


Тогда введённый ранее вектор $ \hat{ v }^2 = -1, \hat{ v } \in \Im $ будет ему всегда перпендикулярен $ \hat{ u } \perp \hat{ v } $ по определению.
Но, как известно, математики для двух мнимых осей нет, только для трёх, поэтому введём сразу ещё один базовый мнимый вектор $ \hat{ w }^2 = -1, \hat{ w } \in \Im $, и определим результаты взаимных операций над ними аналогично кватернионам:

$ \hat{ u }^2 = \hat{ v }^2 = \hat{ w }^2 = \hat{ u } \cdot \hat{ v } \cdot \hat{ w } = -1, \\ \hat{ u } \cdot \hat{ v } = \hat{ w }, \ \hat{ v } \cdot \hat{ w } = \hat{ u }, \ \hat{ w } \cdot \hat{ u } = \hat{ v }, \\ \hat{ v } \cdot \hat{ u } = - \hat{ w }, \ \hat{ w } \cdot \hat{ v } = - \hat{ u }, \ \hat{ u } \cdot \hat{ w } = - \hat{ v }$


Тогда интервал метрики Шварцшильда с мнимыми векторами в явном виде будет:

$ \begin{array}{ccl} ds^2 & = & \color{red}{ (\cos^2 \alpha + \hat{v}^2 \cdot \sin^2 \alpha ) \cdot dt^2 } + \\ & + & \color{green}{ \hat{u}^2 \cdot \cos^2 \alpha \cdot \left( d\rho^2 + \rho^2 \cdot \left[ d\theta^2 + \sin^2 \theta \cdot d\phi^2 \right] \right) } + \\ & + & \color{blue}{\hat{u}^2 \cdot \sin^2 \alpha \cdot \left( \hat{v}^4 \cdot dw^2 + \hat{ v }^2 \cdot w^2 \cdot \left[ d\theta^2 + \sin^2 \theta \cdot d\phi^2 \right] \right) } = \\ & = & \color{red}{ \cos^2 \alpha \cdot dt^2 } + \color{green}{ \hat{u}^2 \cdot \cos^2 \alpha \cdot \left( d\rho^2 + \rho^2 \cdot \left[ d\theta^2 + \sin^2 \theta \cdot d\phi^2 \right] \right) } + \\ & + & \color{red}{ \hat{v}^2 \cdot \sin^2 \alpha \cdot dt^2 } + \color{blue}{ \hat{u}^2 \cdot \sin^2 \alpha \cdot \left( \hat{v}^4 \cdot dw^2 + \hat{ v }^2 \cdot w^2 \cdot \left[ d\theta^2 + \sin^2 \theta \cdot d\phi^2 \right] \right) } = \\ & = & \cos^2 \alpha \cdot \color{green}{ ds_\rho^2 } + \\ & + & \sin^2 \alpha \cdot \color{magenta}{ \hat{ v }^2 } \cdot \left( \color{red}{ dt^2 } + \color{blue}{ (-\hat{ w })^2 \cdot dw^2 + (- \hat{ u })^2 \cdot w^2 \cdot \left[ d\theta^2 + \sin^2 \theta \cdot d\phi^2 \right] } \right) \end{array} $


Можно менять направление тройки $ \hat{ u } \cdot \hat{ v } \cdot \hat{ w } = -1 \rightarrow \hat{ w } \cdot \hat{ v } \cdot \hat{ u } = -1 $ с левого на правое, можно выносить $ \hat{ v }^2 $ (маджента) направо операции некоммутативны. Как ни крути, на языке кватернионов перед всеми пространственными слагаемыми в последней строке будет квадрат мнимого вектора.
Тогда, приняв, что $ ds_\rho^2 = \hat{h}^2 \cdot dt^2 + \hat{u}^2 \cdot \left( d\rho^2 + \rho^2 \cdot d\theta^2 + \rho^2 \cdot \sin^2\theta \cdot d\phi^2 \right)^2 $ квадрат проекции вектора $ d\vec{ s } \in \psi $, принадлежащего расширенному комплексному пространству $ \psi ( \hat{h}, \vec{r} (\hat{u}, \hat{v}, \hat{w}), \hat{\theta}, \hat{\phi} ) = \mathbb{R}^6 \ \dagger $ ), на условно плоское пространство наблюдателя $ \psi_\rho ( \hat{h}, \hat{u}, \hat{\theta}, \hat{\phi} ) = \mathbb{R}^4 $, а $ ds_w^2 $ по аналогии, квадрат проекции этого же вектора внутрь подпространства $ \psi_w ( \hat{h}, \hat{v}, \hat{w}, \hat{\theta}, \hat{\phi} ) = \mathbb{R}^5 $, то движение объекта в гравитационном поле может быть представлено как чистый поворот:

$ ds'^2 = \cos^2 \alpha \cdot ds_\rho^2 + \hat{v}^2 \cdot \sin^2 \alpha \cdot ds_w^2 = \left( e^{\hat{v} \alpha} \cdot d\vec{s} \right)^2 = \left( \mathbf{v} \cdot d\vec{s} \right)^2 \quad \quad (3) $


где $ \mathbf{v} = e^{ \hat{v} \alpha } = \cos \alpha + \hat{v} \cdot \sin \alpha $ ротор, нормализованный вектор поворота. Пока только как индуктивный эскиз от частного к общему.
В третьей статье цикла я постараюсь обобщить модель интервала из тех черт, которые проступили по ходу проведённого изыскания, и других известных свойств явлений природы. Так, чтобы поворотами приводить интервал к известным частным случаям.
$ \dagger $ минимальное количество осей для формализации шесть: время $ \hat{h} $, трёхсоставная радиальная ось $ \vec{r} ( \hat{ u }, \hat{ v }, \hat{ w } ) $, две угловые оси $ \hat{ \theta }, \hat{ \phi } $.
Простыми словами геометрия траектории объекта в сферически симметричном гравитационном поле может быть представлена как поворот четырёхмерного плоского (псевдоевклидова) пространства-времени относительно дополнительных, пятой и шестой мнимых осей.

Заключение


Сначала я подумал, что, возможно, если детально разобраться с единицами измерения угла кривизны $ \alpha $, расчёт относительных траекторий массивных тел через $ (3) $ стал бы гораздо проще и точнее. И к этому несомненно стоит вернуться.
Но, ввиду просматривающейся тенденции, я решил уделить время гораздо более интересному направлению развития теории:
1. Специальная теория относительности. Взаимное движение объектов разных кинетических энергий может быть представлено как движение в континуумах, повёрнутых друг относительно друга (буст).
2. Общая теория относительности. Решение Фридмана. Масштабный фактор расширения Вселенной может быть представлен как угол поворота относительно дополнительной, ненаблюдаемой оси.
3. Общая теория относительности. Решение Шварцшильда. Изменение интервала, соответствующее движению объекта в гравитационном поле, можно представить как поворот относительно дополнительных ненаблюдаемых осей.
Я подумал, что неплохо было бы составить мат. модель, которая обобщала бы все эти повороты. Подобная генерализация, впрессованная в контуры известных вакуумных решений и СТО, могла бы случайно наследовать ряд свойств необходимых, чтобы соответствовать и другим наблюдаемым физическим эффектам. Возможно, она позволила бы взглянуть под другим углом на многие известные явления природы, и дать им интерпретацию. Это, кроме того, что она позволила бы легко обсчитывать комбинированные движения как сумму поворотов. Да много чего ещё там вкусного может быть дух захватывает от этой перспективы.
А с Геометрическим представлением кривизны в метрике Шварцшильда локально я вроде закончил.
Читателей очень прошу, кому не лень, проверить математику. Я её люблю, она взаимна, но она царица, а я всего лишь человек могу ошибаться.
Подробнее..
Категории: Научно-популярное , Физика , Математика , Космология , Кривизна , Пространство , Гиперпространство , Общая теория относительности , Эйнштейн , Гравитация , Шварцшильд , Теория относительности , Решение ото

Перевод Спросите Итана по какой фундаментальной причине E mc?

23.05.2021 20:21:44 | Автор: admin

Альберт Эйнштейн в 1920 году. Хотя он и совершил множество прорывов в физике, от специальной и общей теорий относительности до фотоэлектрического эффекта и статистической механики, многие задачи он решить не сумел. Самым его знаменитым уравнением остаётся E = mc.

Спросите любого человека, даже не разбирающегося в науке, о достижениях Эйнштейна, и вам приведут в пример самое его знаменитое уравнение: E = mc. Проще говоря, оно означает, что энергия равняется массе, перемноженной с квадратом скорости света. И это очень многое говорит о нашей Вселенной. Единственное уравнение говорит о том, сколько энергии содержится в массивной частице в состоянии покоя, и сколько энергии требуется для создания частиц и античастиц. Оно говорит нам о том, сколько энергии высвобождается в ядерных реакциях, и сколько энергии порождает аннигиляция материи с антиматерией.

Но почему? Почему энергия равняется массе, перемноженной с квадратом скорости света? Почему не как-то иначе? Об этом спрашивает наш читатель:

Уравнение Эйнштейна потрясающе элегантное. Но реальна ли его простота, или же только кажется? Выводится ли оно напрямую из эквивалентности энергии любой массы и квадрата скорости света (а это вообще кажется удивительным совпадением)? Или оно существует только потому, что его члены определены удобным способом?

Отличный вопрос. Давайте исследуем самое знаменитое уравнение Эйнштейна, и посмотрим, почему оно не могло быть другим.


Подготовка к испытаниям ракеты с ядерным двигателем, 1967. Она работает на преобразовании массы в энергию, в основе которого лежит знаменитое уравнение E = mc.

Для начала нужно кое-что понять касательно энергии. Её очень сложно определить, особенно далёкому от физики человеку. Навскидку мы можем придумать несколько примеров.
  • Существует потенциальная энергия, т.е. некая форма сохранённой энергии, которую можно освободить. Например, бывает гравитационная потенциальная энергия, когда мы поднимаем массу на большую высоту. Химическая потенциальная энергия, хранящаяся в таких молекулах, как сахара, и способная производить окисление. Электрическая потенциальная энергия, когда накопленный в аккумуляторе или конденсаторе заряд можно разрядить, высвобождая её.
  • Существует кинетическая энергия, присущая движущимся объектам.
  • Существует электрическая энергия кинетическая энергия, присущая движущимся зарядам и электрическим токам.
  • И ядерная энергия, или энергия, высвобождаемая переходами атомов в более стабильные состояния.


И, конечно же, множество других типов. Энергия это одна из тех вещей, которые мы узнаем, когда увидим. Но физикам требуется более универсальное определение. Одно из лучших такое: извлечённая или извлекаемая энергия это количественная оценка нашей способности произвести работу.


Фотоэлектрический эффект описывает ионизацию электронов фотонами в зависимости от длин волн отдельных фотонов, а не от интенсивности света, суммарной энергии или какого-либо ещё свойства. Если у кванта света достаточно энергии, он может взаимодействовать с электроном, ионизировав его, выбив его из материала, что даст сигнал, который можно обнаружить. Такие фотоны переносят энергию и выполняют работу над ударяемыми ими электронами.

У работы есть своё физическое определение: это сила, прикладываемая в направлении, совпадающем с направлением движения предмета, умноженная на расстояние его перемещения. Поднятие штанги на определённую высоту требует провести работу против силы гравитации, и увеличивает гравитационную потенциальную энергию. Отпустив штангу, мы преобразуем её гравитационную потенциальную энергию в кинетическую. Ударяющая пол штанга преобразует кинетическую энергию в комбинацию из тепловой, механической и звуковой энергии. Энергия в этих процессах не создаётся и не уничтожается, а преобразуется из одной формы в другую.

Большинство людей размышляют о формуле E = mc в терминах анализа размерностей. Они говорят: так, энергия измеряется в Джоулях, а Джоуль это килограмм на метр в квадрате на секунду в квадрате. Поэтому, чтобы превратить массу в энергию, нужно умножить это на метр в квадрате, делённый на секунду в квадрате. При этом у нас есть фундаментальная константа с размерностью метр/секунда. Эти рассуждения разумны, но не достаточны.


Фотографии с Тринити, первого в мире испытания технологии ядерного оружия. Показана ситуация спустя 16, 25, 53 и 100 мс после зажигания. Самая высокая температура достигается в самом начале взрыва, до того, как его объём многократно вырастает.

Ведь вы можете измерять любую скорость в метрах в секунду, а не только скорость света. Кроме того, природе никто не запрещает выдать пропорциональную константу какой-нибудь множитель типа , , 2, и т.п., чтобы сделать уравнение верным. Чтобы понять, почему уравнение должно выглядеть, как E = mc, и почему других вариантов быть не может, нам надо представить физическую ситуацию, в которой можно будет различить разные интерпретации. Такой теоретический инструмент известен, как мысленный эксперимент (или gedankenexperiment, как сказал бы Эйнштейн), и стал одной из великих идей, появившихся в голове Эйнштейна и укоренившихся в научном мейнстриме.

Мы можем представить, что у частицы есть энергия, присущая её массе покоя, и энергия её движения кинетическая. Можно представить, что частица начала свой путь, находясь высоко в гравитационном поле, то есть с большим запасом потенциальной энергии, но изначально не двигалась. Если мы её уроним, потенциальная энергия превратится в кинетическую, а энергия массы покоя останется той же. Перед самым ударом о землю никакой потенциальной энергии у неё не останется только кинетическая и энергия массы покоя, какие бы они ни были.


У обозначенной оранжевым частицы, покоящейся над поверхностью земли, не будет кинетической энергии, но будет большой запас потенциальной. Если её отправить в свободное падение, она приобретёт кинетическую энергию, в которую превратится потенциальная.

Теперь добавим ещё одну идею: что у всех частиц есть двойники-античастицы, и что когда они сталкиваются друг с другом, то аннигилируют, выделяя чистую энергию.

Да, E = mc описывает взаимоотношение массы и энергии, включая количество энергии, необходимое для создания из ничего пар частица-античастица, и то, сколько энергии вы получите, когда такая пара аннигилирует. Но мы пока этого не знаем, мы хотим это доказать!

Давайте представим, что у нас не одна частица находится высоко в гравитационном поле, а сразу и частица, и античастица, и они готовы упасть. Рассмотрим два разных сценария развития, и изучим их последствия.


Появление пар частица-античастица (слева) из чистой энергии реакция полностью обратимая (справа), они могут аннигилировать, превратившись в энергию. Но для многих систем частиц обратимость не гарантирована.

Сценарий 1: частица и античастица падают, и аннигилируют прямо перед ударом о землю. Ситуация похожа на описанную ранее, просто мы её удвоили. И частица, и античастица начинали с некоего количества энергии массы покоя. Мы не знаем, сколько её было, просто знаем, что у частицы и античастицы они одинаковые, поскольку массы частиц идентичны массам соответствующих античастиц.

Теперь они обе падают, превращая потенциальную гравитационную энергию в кинетическую, в дополнение к их энергии массы покоя. Как и в предыдущем случае, перед ударом о землю вся их энергия заключена в двух видах энергии массы покоя и кинетической. Только теперь перед самым столкновением они аннигилируют, превращаясь в два фотона, общая энергия которых должна равняться сумме энергий массы покоя и кинетических энергий обеих частиц.

Однако для фотона, массы не имеющего, энергия описывается одним только импульсом, помноженным на скорость света: E = pc. Какой бы ни была энергия обеих частиц перед столкновением с землёй, энергия этих фотонов должна в сумме давать сумму энергию частиц.


Если пара частица-античастица аннигилирует в чистую энергию (два фотона), имея в запасе много гравитационной потенциальной энергии, то в энергию фотона перейдёт только масса покоя (оранжевый). Если уровнить эти частицы вниз, чтобы они аннигилировали непосредственно перед ударом, у них будет больше энергии, что приведёт к появлению более синих фотонов.

Сценарий 2: частица и античастица аннигилируют в чистую энергию, а потом падают вниз до земли в виде фотонов с нулевой массой покоя. Тогда вся их энергия массы покоя превратится в энергию фотонов.

Получается, что в данном случае общая энергия этих фотонов, у каждого из которых есть энергия E = pc, должна быть равной сумме энергий масс покоя частицы и античастицы.

Теперь представим, что эти фотоны добрались до поверхности планеты, и после этого мы измеряем их энергию. По закону сохранения, их энергия должна равняться энергии фотонов из первого сценария. Значит, фотон должен набирать энергию, падая в гравитационном поле. Это явление известно, как гравитационный синий сдвиг. Кроме того, из этого следует идея о том, что масса покоя частицы должна равняться E = mc.


Когда квант излучения покидает гравитационное поле, его частота должна испытать красный сдвиг, чтобы энергия сохранилась. При падении частота должна сдвинуться в синий диапазон. Это имеет смысл, только если гравитация связана не только с массой, но и с энергией. Гравитационное красное смещение одно из ключевых предсказаний Общей теории относительности Эйнштейна. Но его только недавно проверили в окружении с такими сильными полями, как центр нашей Галактики.

Есть только одно определение энергии, подходящее ко всем частицам, и имеющим, и не имеющим массу, и удовлетворяющее сценариям 1 и 2, которые должны выдать одинаковые результаты. E = (m2c4 + p2c2). Посмотрим, что с ним будет в разных ситуациях.

  • У массивной частицы в состоянии покоя и без импульса энергия будет равной (m2c4), то есть, E = mc.
  • Безмассовая частица обязана двигаться, а её масса покоя равна нулю. Её энергия равняется (pc), или E = pc.
  • У массивной частицы, движущейся значительно медленнее скорости света, импульс можно записать как p = mv, и тогда её энергия становится равной (mc4 + mvc). Это можно переписать как E = mc * (1 + v/c), если v значительно меньше c.


Если вам незнаком последний член, не расстраивайтесь. Если v очень мало по сравнению с c, вы можете выполнить разложение в ряд Тейлора, и получите E = mc [1 + (v/c) + ...]. Взяв первые два члена, вы получите E = mc + mv: массу покоя плюс старую добрую, нерелятивистскую формулу кинетической энергии.


Вверху: фотон движется внутри коробки. В середине: коробка поглотила фотон. Внизу: фотон переиспущен в противоположном направлении. Из такого эксперимента, принимая законы сохранения энергии и импульса, можно вывести знаменитое E = mc.

Конечно, так выводить E = mc не стоит, но это мой любимый способ иллюстрации этой задачи. Могу порекомендовать ещё три способа иллюстрации, а также описание того, как это сделал сам Эйнштейн. Второй моей любимой иллюстрацией вывода этой формулы будет рассмотрение фотона, движущегося в неподвижной коробке с зеркалом на одной из стенок.

Когда фотон сталкивается с зеркалом, он на некоторое время поглощается, в результате чего коробка должна приобрести немного энергии, и начать двигаться в том же направлении, что и фотон это единственный способ сохранить энергию и импульс.

После переиспускания фотон движется в противоположном направлении, поэтому коробке (потерявшей немного массы после переиспускания фотона) нужно двигаться вперёд ещё быстрее.

И хотя тут много неизвестных, в такой ситуации можно написать множество уравнений, которым необходимо совпадать. Общая энергия всех частей системы и общий момент должны быть эквивалентными. Если решить эти уравнения, получится только одно определение энергии массы покоя: E = mc.


Эйнштейн выводит Специальную теорию относительности перед зрителями, 1934 год. Если потребовать сохранения энергии и применить теорию относительности к подходящим системам, необходимо, чтобы E = mc.

Можно представить себе совсем не такую вселенную, в которой мы живём. Возможно, там не сохраняется энергия и тогда формула E = mc может не быть универсальным выражением массы покоя. Возможно, мы могли бы нарушить закон сохранения импульса тогда наше определение общей энергии, E = (m2c4 + p2c2), не было бы верным. А если бы там не действовала Общая теория относительности, или импульс и энергия фотона не были бы связаны соотношением E = pc, тогда E = mc не была бы универсальной формулой для массивных частиц.

Но в нашей Вселенной энергия сохраняется, и работает Общая теория относительности. Поэтому нужно просто подобрать подходящие условия эксперимента. И даже не проводя его на самом деле, можно прийти только к одному непротиворечивому значению для энергии массы покоя частицы. Можно представить себе вселенную, в которой взаимоотношение массы и энергии были бы другими, но она была бы совсем непохожей на нашу. И это не просто удобное определение это единственный способ сохранить энергию и импульс с имеющимися у нас законами физики.
Подробнее..
Категории: Научно-популярное , Физика , Эйнштейн , Энергия , Теория относительности , Спросите итана , Масса покоя , Закон сохранения

Категории

Последние комментарии

  • Имя: Макс
    24.08.2022 | 11:28
    Я разраб в IT компании, работаю на арбитражную команду. Мы работаем с приламы и сайтами, при работе замечаются постоянные баны и лаги. Пацаны посоветовали сервис по анализу исходного кода,https://app Подробнее..
  • Имя: 9055410337
    20.08.2022 | 17:41
    поможем пишите в телеграм Подробнее..
  • Имя: sabbat
    17.08.2022 | 20:42
    Охренеть.. это просто шикарная статья, феноменально круто. Большое спасибо за разбор! Надеюсь как-нибудь с тобой связаться для обсуждений чего-либо) Подробнее..
  • Имя: Мария
    09.08.2022 | 14:44
    Добрый день. Если обладаете такой информацией, то подскажите, пожалуйста, где можно найти много-много материала по Yggdrasil и его уязвимостях для написания диплома? Благодарю. Подробнее..
© 2006-2024, personeltest.ru