Математическая статистика

Есть одна довольно любопытная задачка, она уже давно вошла в математический фольклор, а так же стала излюбленным испытанием на собеседованиях. Ее условия просты, а решение, кажется напрашивается само собой, однако не будем торопиться с выводами. Берите карандаш, чистый лист бумаги, усаживайтесь поудобней и давайте во всем разбираться.

В чем же, собственно, задача

Итак представьте, что Вы приехали в абсолютно незнакомый город и первый трамвай, который вам там повстречался, следовал под номером 17. Как оценить, сколько всего в этом городе трамвайных маршрутов?

Для простоты считайте, что трамвайные маршруты в городе пронумерованы без пропусков числами от 1 до N и изначально каждое из этих чисел с равными шансами могло оказаться номером трамвая, которого вы бы увидели первым.

Впервые задачу о Случайном трамвае я услышал от Николая Николаевича Васильева, моего знакомого питерского математика. Тогда же он поделился со мной наблюдением, что среди тех, кому он рассказывал эту задачу, а затем просил дать ответ не задумываясь, большинство людей назвало число 34, то есть "x2" от 17. На моем опыте самым экстравагантным был ответ моего товарища с мехмата: 17. Только через неделю я догадался, что им двигал спавший где-то на подкорке его мозга принцип максимизации правдоподобия. Хорошо, но 17 и 34, другими словами "x1" и "x2" это наивные и необдуманные ответы, а какой тогда правильный ответ, и вообще, существует ли он у этой задачи.

Подводные камни и область фантазии
Почему же стоит сомневаться насчет существования универсально-правильного ответа? К такой мысли легко прийти, если рассмотреть несколько простых, пускай и вымышленных вселенных. К примеру представьте, что на Земле в каждом городе ровно по 30 трамвайных маршрутов. Будет ли в этой вселенной 30 единственно верным ответом? Теперь представьте, что в другой вселенной на Земле 1000 городов, причем в 999 из них действует по 30 трамвайных маршрутов, а в оставшемся одном их ровно 17. Какой на сей раз ответ будет правильным и как на него повлияет то обстоятельство, что городов с 30-ю маршрутами очень много, а с 17-ю всего один? Сразу скажу, что пользоваться вероятностными соображениями здесь очень трудно, ведь человек, которого просят оценить число маршрутов, не знает, был ли город, в котором он сейчас гостит, выбран на карте случайно, или в этом выборе кроется некая причина и присутствует чей-то расчет.

Принцип крайнего математического пессимизма

Несмотря на заявленные трудности, в математике имеется принцип, при помощи которого для нашей задачи можно дать ответ, остающийся осмысленным даже в самых причудливых мирах.
Когда дело касается игр, этот принцип называют максимизацией гарантированного выигрыша,
и чтобы понять в чем кроется его суть, давайте рассмотрим один простой пример.

Представьте себе игру: скрытно от вас в один из своих кулаков я прячу маленький предмет, пусть это будет сухая горошина, затем вытягиваю руки вперед и прошу вас угадать, в какой из них эта горошина находится. Пусть у нас есть время, чтобы сыграть очень долгую партию игр, причем изначально вам не известно, пытаюсь ли я вас в ней обыграть, стараюсь намеренно поддаться, или сохраняю безразличие к вашему успеху. Предположим, что перед вами стоит цель: выиграть как можно больше игр. Какой стратегии вам в таком случае стоило бы придерживаться?

Для начала давайте попробуем проанализировать, преимущества и недостатки следующих четырех простеньких стратегий:

1. Всегда выбирать правую руку.
2. Начать с правой, а затем выбирать ту руку, в которой горошина была найдена в последний раз.
3. В каждой игре перед тем, как сделать выбор, бросить на стол игральную кость. Если выпало 1 или 2, то выбрать правую руку, на 3, 4, 5 и 6 левую.
4. Как и в предыдущей стратегии, в каждой игре бросить кость. В тех случаях, когда выпавшая грань оказалась четной, выбрать правую, а когда нечетной левую.

Если вы решите воспользоваться стратегией 1) и при этом я буду прятать горошину всегда в правой руке, то все игры завершаться в вашу пользу. Можно сказать, что сценарий развития партии, при котором я прячу горошину исключительно в правую руку, является для 1)наилучшим. Однако в своем наихудшем сценарии, сценарии, где я прячу горошину исключительно в левой руке, стратегия 1) не позволит вам выиграть ни одной игры, какой бы долгой не была наша партия.

Легко догадаться, что стратегия 2) страдает тем же пороком, а именно в наихудшем для нее сценарии, когда я начинаю с левой руки и затем в каждой из следующих игр чередую руки, она не позволит вам выиграть ни разу, как бы долго не длилась наша партия.

Займемся теперь стратегией, которая идет в нашем списке третьей. Если вы ею воспользуетесь, то ваши шансы на победу в каждой игре, где горошина будет спрятана в правую руку, составят 1/3, а в играх, в которых горошина будет находится в левой, 2/3. Понятное дело, что наихудший сценарий для 3) это, когда я имею привычку прятать горошину исключительно в правой руке, однако даже в этом случае в любой достаточно длинной партии игр, примерно треть из них завершится вашей победой. Теоретически вам конечно может и не повезти, и правильную руку вы не отгадаете ни разу, но практически, скажем в партии из 1000 игр, почти не вероятно, чтобы количество ваших побед было меньше, чем 333 4 (1000 1/3 2/3), то есть меньше чем 333 60, а в партии из миллиона игр возможный процент отличий будет еще меньше. По сути, выбрав стратегию 3), вы тем самым гарантируете себе, что примерно треть от игр партии останутся за вами.

Если вы воспользовались четвертой в списке стратегией, то наша игра приобретает интересную особенность: по сути для вас перестает быть важным, на сей раз я спрятал горошину в правой руке или положил ее в левую, потому как в обеих ситуациях ваши шансы на победу будут одинаковы и составят ровно 50%. Можно даже сказать, любая намеченная мною очередность рук, где я собираюсь прятать горошину, для вас будет является одновременно и наилучшим и наихудшим сценарием развития партии. Получается, что при любых раскладах в достаточно долгой партии игр примерно половина из них должны закончиться вашей победой, в этом смысле стратегия 4) дает вам самые большие гарантии, по сравнению со всеми остальными стратегиями, которые мы уже успели здесь рассмотреть.

Принцип максимизации гарантированного выигрыша предписывает вам перебрать все возможные стратегии игры, для каждой из них вычислить величину выигрыша в наихудшем для нее сценарии и объявить оптимальной ту стратегию, для которой величина этого выигрыша окажется наибольшей. Можно показать, что в игре с угадыванием местоположения горошины, оптимальной, а не только лучшей из списка, является стратегия под номером 4. По своей сути максимизация гарантированного выигрыша аналогична жизненному кредо тех людей, которые всегда склонны рассчитывать на худшее, но при этом все еще пытаются как-то улучшить свое положение в жизни.

Задача о случайном трамвае приобретает свой окончательный вид

Формализм
Чтобы воспользоваться принципом максимизации гарантированного выигрыша, представьте, что судьба играет с вами в игру: она раз за разом посылает вас в неизвестный город, расположенный в какой-то неизвестной вселенной, ждет пока вы не повстречаете там первый трамвай, а затем вопрошает, сколько же в этом городе всего трамвайных маршрутов. Будем считать, что ваш ответ считается приемлемым и игра заканчивается в вашу пользу, если только названное вами число отличается менее чем в два раза от истинного, причем как в большую, так и в меньшую стороны. Будем также считать, что это очень долгая партия игр, длинною в целую жизнь.

Теперь вполне правомерно задать вопрос: Какая стратегия в описанной игре будет для вас оптимальной в том смысле, что сможет обеспечить максимальное число гарантированно приемлемых ответов?

Подробный анализ простейших стратегий
В качестве первого боя с только что поставленной задачей попытаемся выяснить, насколько хороши для нее наивные стратегии "x1" и "x2".

Итак, судьба забросила нас в очередной незнакомый нам город. Как и прежде, буква $inline$N$inline$ обозначает количество трамвайных линий в этом городе. По условию все числа от $inline$1$inline$ до $inline$N$inline$ с равной вероятностью могут оказаться номером маршрута $inline$k$inline$, по которому будет следовать первый подмеченный нами трамвай.

Согласно стратегии "x1" оценкой $inline$V$inline$ для числа $inline$N$inline$ должно быть само $inline$k$inline$. Понятное, что $inline$k$inline$ никогда не будет больше $inline$N$inline$, поэтому не может оказаться так, чтобы $inline$V$inline$ была больше $inline$2N$inline$. Следовательно наша оценка будет неприемлемой только в одном случае: если $inline$V$inline$, то есть $inline$k$inline$, окажется меньше, чем $inline$N/2$inline$. Вероятность получить $inline$k$inline$ меньшее $inline$N/2$inline$ при нечетных$inline$N$inline$ не превосходит 50%, а при четных равна им. Отсюда следует, что при использовании стратегии "x1" в очень длинной партии игр по крайней мере (примерно) половина сделанных оценок гарантированно окажутся приемлемыми, какой бы там сценарий не уготовила судьба.

Теперь предположим, что мы решили использовать стратегию "x2". По правилам этой стратегии, увидев на трамвае номер $inline$k$inline$, мы должны в качестве $inline$V$inline$ назвать число $inline$2k$inline$. Как и в предыдущем случае, наша оценка никогда не превзойдет $inline$2N$inline$, и поэтому неприемлемой она будет считаться только при одном условии, если ее значение меньшее, чем $inline$N/2$inline$. В то же время, $inline$V$inline$ будет меньше $inline$N/2$inline$, только если номер трамвая $inline$k$inline$ окажется меньше, чем $inline$N/4$inline$. Вероятность последнего события для городов с $inline$N$inline$ кратным 4-ем равна $inline$1/4$inline$, а для остальных городов и того меньше. Следовательно, если мы решаем придерживаемся стратегии "x2", то тем самым обретаем гарантию, что в любой долгой партии игр по крайней мере (примерно) 3/4 всех наших ответов окажутся приемлемы независимо от того, насколько превратно поведет себя с нами судьба.

Сквозь тернии к звездам
Перед тем, как приступить к главной части повествования, где мы займемся поисками оптимальных стратегий, я слегка видоизменю условия задачи и буду считать, что $inline$N$inline$, $inline$V$inline$ и $inline$k$inline$ могут теперь принимать не только натуральные, но и любые действительные значения, большие нуля. Этот шаг необходим, чтобы избавиться от связанных с дискретностью надоедливых оговорок и скучного перебора особых случаев. Конечно, сейчас еще трудно представить себе город, в котором есть трамваи со всеми номерами от 0 до , однако этого вам и не понадобится. У нашей задачи в ее новой непрерывной модификации имеется простая и вполне реалистичная модель.

Представьте себе, что некто взял полоску фотографической пленки длинной $inline$N$inline$см и решил пронаблюдать за тем, как на ней будут оставлять свой след приходящие из космоса частицы. В масштабах эксперимента плотность вероятности попадания частиц на пленку будет описываться равномерным распределением на отрезке $inline$[0,\,N]$inline$. В этом опыте экспериментатор сообщает вам расстояние $inline$k$inline$ между левым краем пленки и точкой, куда угодила первая зарегистрированная частица. Как и прежде, от вас требуется дать приемлемую оценку $inline$V$inline$ для неизвестного вам $inline$N$inline$, то есть такую оценку, которая отличается от $inline$N$inline$ не более чем в два раза, как в большую, так и в меньшую стороны. Как и прежде, судьба ведет с вами долгую партию игр, каждый раз решая, каково будет $inline$N$inline$ в очередной игре.

В качестве простого упражнения покажите, что несмотря на изменившиеся условия стратегия "x1" по-прежнему гарантирует вам примерно 50%, а стратеги "x2" все те же примерные 75% приемлемых оценок соответственно, вне зависимости от того, какой сценарий выберет судьба.

Долгий путь к совершенству

Предварительный отсев
Наконец-то все приготовления завершены и в этом параграфе мы можем заняться поисками оптимальных стратегий. Для простоты, правда, мы будем рассматривать не все стратегии, а ограничимся теми, в которых оценка $inline$V$inline$ представима, как $inline$f(k)$inline$, где $inline$f()$inline$ это некоторая действительнозначная функция, определенная на интервале $inline$(0,\ +\infty)$inline$.

Представьте теперь, что в одном эксперименте расстояние от места попадания частицы до левого края фотопленки было равным $inline$k_1$inline$, а в другом эксперименте $inline$k_2$inline$, причем $inline$k_1<k_2$inline$. Не будет ли тогда разумным, длине фотопленки в первом эксперименте дать меньшую оценку, чем во втором. Если так, то из неравенства $inline$k_1<k_2$inline$ всегда должно следовать неравенство $inline$f(k_1)<f(k_2)$inline$, другими словами, функция $inline$f()$inline$ должна быть строго возрастающей. Не менее разумным выглядит предположение, что для близких по значению $inline$k_1$inline$ и $inline$k_2$inline$ оценки $inline$V_1=f(k_1)$inline$ и $inline$V_1=f(k_2)$inline$ тоже должны быть близки, то есть, функция $inline$f()$inline$ должна быть непрерывной.

Если проанализировать, какие ответы мы считаем приемлемыми, то получится еще одно
ограничение на $inline$f()$inline$. Смотрите, в нашем понимании задачи $inline$V$inline$ приемлема в том (и только в том случае), когда $inline$N/2\le f(k)\le2N$inline$. Расстояние $inline$k$inline$ между засвеченным космической частицей пятном и левым краем фотографической пленки никогда не превосходит длину пленки $inline$N$inline$, отсюда непосредственным образом получаем неравенство: $inline$2k\le2N$inline$. Из последнего неравенства следует, что было бы неразумно, узнав от экспериментатора расстояние $inline$k$inline$, оценивать $inline$N$inline$ числом $inline$V$inline$ меньшим $inline$2k$inline$. Действительно, если мы увеличим оценку $inline$V$inline$ до $inline$2k$inline$, то тем самым точно не сделаем ее чрезмерно большой, однако в тех случаях, когда $inline$V$inline$ изначально была неприемлемо малой, подобное переопределение способно ее даже исправить. Таким образом, в процессе поиска оптимальных стратегий нам достаточно рассмотреть только те функций $inline$f(k)$inline$, значения которых при всех $inline$k>0$inline$ подчинены неравенству
$inline$f(k)\geq2k$inline$.

Ее величество формула
Сейчас мы займемся тем, что для произвольной стратегии постараемся выразить величину гарантируемого ею выигрыша в виде некой общей аналитической формулы.

Итак, в очередном эксперименте по регистрации космических частиц используется фотопленка длины $inline$N$inline$, $inline$k$inline$ удаление точки попадания первой частицы от ее (пленки) левого края, а $inline$V=f(k)$inline$ наша оценка для $inline$N$inline$. Пусть эксперименту только предстоит состояться, какова тогда вероятность, что $inline$V$inline$ окажется приемлемой по отношению к $inline$N$inline$? Самое большое значение $inline$V$inline$, когда она еще считается приемлемой, это $inline$2N$inline$, самое маленькое $inline$N/2$inline$.

Поскольку $inline$f()$inline$ строго возрастает и непрерывна, то существует обратная к ней функция $inline$f^{-1}\left(v\right)$inline$, которая также строго возрастает и непрерывна. Для значений $inline$f()$inline$ всюду выполняется неравенство $inline$f(k)\geq2k$inline$, поэтому для значений $inline$f^{-1}()$inline$ должно выполнятся двойственное неравенство: $inline$f^{-1}\left(v\right)\le 1/2 v$inline$ (рис 1)


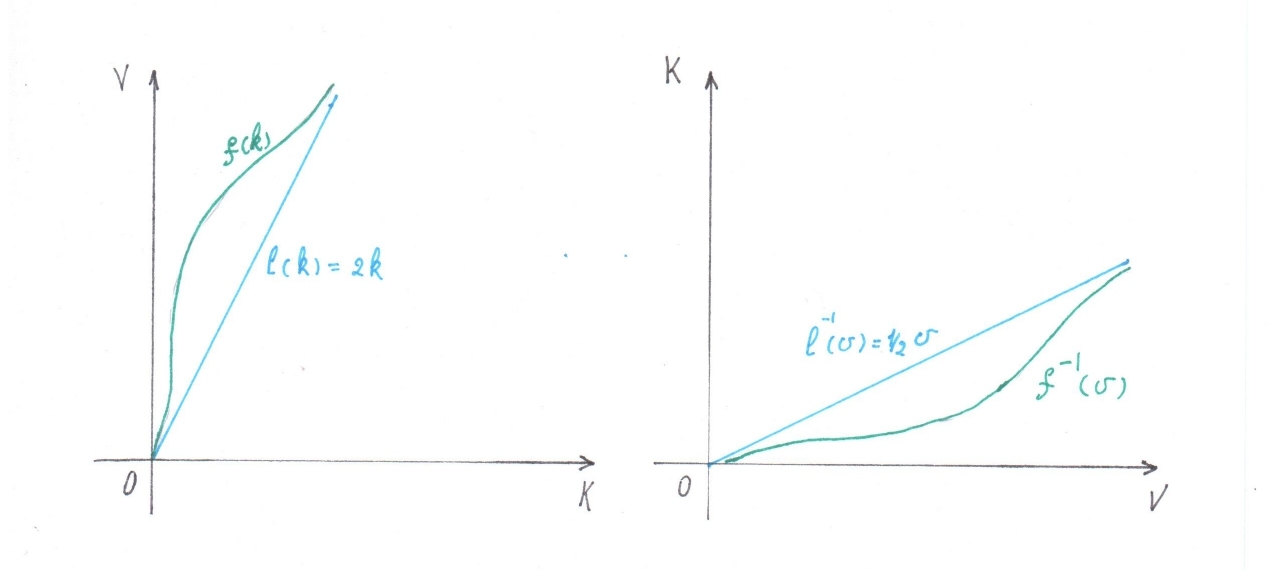
рис 1

Теперь нетрудно сообразить, что максимальным значением $inline$k$inline$, дальше которого $inline$V$inline$ становится уже неприемлемо большой, является $inline$k_{sup}=f^{-1}\left(2N\right)$inline$. Это следует из того, что $inline$f^{-1}\left(\right)$inline$ строго возрастает и $inline$k_{sup}=f^{-1}\left(2N\right)\le 2N$inline$. Аналогично, минимальным значением $inline$k$inline$, меньше которого $inline$V$inline$ становится неприемлемо малой, является $inline$k_{inf}=f^{-1}\left(N/2\right)$inline$. Из двух последних утверждений следует, что $inline$V$inline$ будет приемлемой по отношению к $inline$N$inline$ в том (и только в том) случае, если расстояние $inline$k$inline$ между засвеченным пятном и левым краем пленки окажется заключенным между $inline$k_{inf}$inline$ и $inline$k_{sup}$inline$. Вероятность последнего события, обозначим ее как $inline$p_{success}(f,\ N)$inline$, равна:

$$display$$\frac{k_{sup}-\ k_{inf}\ }{N}$$display$$

или более подробно:

$$display$$p_{success}(f,\ N)=\ \frac{f^{-1}\left(2N\right)-\ f^{-1}\left(N/2\right)\ }{N}$$display$$

Должно быть очевидно, что наихудшим для для $inline$f$inline$ сценарием будет последовательность таких экспериментов, в каждом из которых длинна фотографической пленки $inline$\bar{N}$inline$ минимизирует значение $inline$p_{success}(f,\ N)$inline$. Отсюда следует, что в очень длинных последовательностях экспериментов доля приемлемых ответов, гарантированная оценкой $inline$f(k)$inline$, будет даваться выражением:

$$display$${\rho\left(f\right)={inf}_N[\ p}_{success}(f,\ N)]$$display$$

Теперь мы можем утверждать, что любая оптимальная стратегия должна максимзировать $inline$\rho\left(f\right)$inline$, другими словами, $inline$\varphi(k)$inline$ будет оптимальной в том и только в том случае, если:

$$display$${inf}_N[p_{success}\left(\varphi,\ N\right)]={sup}_f\ {inf}_N[p_{success}\left(f,\ N\right)]$$display$$

.
Итак, проблема отыскания оптимальных оценок свелась к вопросу о том, как выглядит функция $inline$\varphi(k)$inline$, которая доставляет выражению

$$display$$(*)\ \ \ \ \ \ inf_N\left[\frac{f^{-1}\left(2N\right)-f^{-1}\left(N/2\right)}{N}\right]$$display$$

максимум в классе всех непрерывных строговозрастающих функций, определенных
на интервале (0, +), графики которых лежат не ниже $inline$l(k)=\ 2k$inline$. Не правда ли, что в такой постановке задача может показаться пугающе сложной? Я думаю, для вас это прозвучит неожиданным, но ответ на нее изысканно прост. Давайте вместе попытаемся его угадать.

Искусство правдоподобных рассуждений
Пожалуй, самое простое, с чего можно начать это выяснить, какая из функций вида $inline$f(k)=\ \lambda\cdot k$inline$ (здесь $inline$\lambda$inline$ любое действительное число 2) доставляет выражению (*) самое большое значение. Обратной для $inline$f(k)=\ \lambda\cdot k$inline$ служит функция $inline$f^{-1}\left(v\right)=\lambda^{-1}\cdot v$inline$, подставляя ее в выражение для $inline$p_{success}$inline$, имеем:

$$display$$p_{success}\left(N,\lambda\right)=\ \frac{\lambda^{-1}\cdot2N-\lambda^{-1}\cdot N/2}{N}=\frac{3}{2}\ \cdot\ \lambda^{-1}\ $$display$$

Как вы видите, $inline$p_{success}$inline$ не зависит от $inline$N$inline$ и принимает тем большее значение, чем меньшим по величине было $inline$\lambda$inline$. Таким образом, в классе функций $inline$f(k)=\ \lambda\cdot k$inline$, $inline$\lambda\geq2$inline$ наибольшее значение выражению (*), придает уже знакомая нам по функция $inline$l(k)=\ 2k$inline$.

Давайте теперь подумаем, что произойдет, если отсчитывать расстояние не в сантиметрах, а, скажем, метрах, дюймах или световых годах как тогда изменится вид функции $inline$\varphi$inline$ оптимальной оценки?
Пусть в сантиметрах оценка $inline$V$inline$ имеет вид $inline$V_{cm}=\ f_{cm}(k_{cm})$inline$, а $inline$V_m$inline$ и $inline$k_m$inline$ те же самые величины, выраженные в метрах, тогда:

$$display$$V_m=\frac{1}{100}V_{cm}=\frac{1}{100}f_{cm}({100\cdot k}_m)=\ f_m(k_m)$$display$$

В общем случае мы будем иметь дело со шкалой длин $inline$A$inline$ и шкалой длин $inline$B$inline$, которая получается из $inline$A$inline$ умножением на коэффициент $inline$\mu_{AB}$inline$. Каждая оценка $inline$V(k)$inline$ может быть вычислена как в единицах шкалы $inline$A$inline$, так и в единицах шкалы $inline$B$inline$. Пусть $inline$f_A(k_A)$inline$ ее представление в единицах шкалы $inline$A$inline$, а $inline$f_B(k_B)$inline$ представление в единицах шкалы $inline$B$inline$, тогда:

$$display$$f_B(t)=\mu_{AB}\cdot f_A({\mu_{AB}}^{-1}\cdot t)$$display$$

Вид последнего уравнения говорит о том, что функции $inline$f_A(t)$inline$ и $inline$f_B(t)$inline$ скорей всего различны ($inline$t$inline$ в данном случае это действительная переменная с нейтральным смыслом).

Как вы считаете, правдоподобно ли, что мы и какой-нибудь представитель далекой космической цивилизации получим для решаемой здесь задачи разные ответы лишь потому, что у нас с ним разные единицы измерения длины? Наверное, нет! Отсюда следует, что для любого $inline$\mu>0$inline$ и любой функции $inline$\varphi(t)$inline$, которая максимизирует выражение $inline$(*)$inline$, функция $inline$\psi(t)=\mu\cdot\varphi(\mu^{-1}\cdot t)$inline$ также должна максимизировать $inline$(*)$inline$. Если вдруг $inline$\varphi(t)$inline$ является единственной оптимальной для $inline$(*)$inline$ функцией, то при всех $inline$t>0$inline$ и $inline$\mu>0$inline$ выполняется тождество:

$$display$$\varphi(t)=\mu\cdot\varphi(\mu^{-1}\cdot t)$$display$$

Положив в этом тождестве $inline$\mu=t$inline$, мы тем самым находим вид функции $inline$\varphi$inline$:

$$display$$\varphi(t)=t\cdot\varphi(t^{-1}\cdot t)=t\cdot\varphi(1)$$display$$

Смотрите, что выходит: если все наши многочисленные предположения верны, то оптимальная функция $inline$\varphi(t)$inline$ принадлежит классу функций $inline$f(k)=\ \lambda\cdot k$inline$, но ранее мы уже выяснили, что внутри указанного класса максимальное значение выражению $inline$(*)$inline$ придает функция $inline$l(k)=\ 2k$inline$. Неужели оптимальной стратегией является "x2"?

Строгие выводы: оптимальность x2
Хорошо, у нас есть много намеков на то, что оценка, заданная функцией $inline$l(k)=\ 2k$inline$, является оптимальной. Давайте докажем эту гипотезу строго, а еще установим, при каких условиях других оптимальных оценок нет.

Возьмем произвольную непрерывную строго возрастающую функцию $inline$f(k)$inline$, удовлетворяющую неравенству $inline$f(k)\le2k$inline$, фиксируем некоторое $inline$v_0$inline$ из области ее значений и попытаемся для начала выяснить, какой геометрический смысл скрывается за величиной $inline$p_{success}\left(f,\ v_0\right)$inline$.


рис 2

Если на графике функции $inline$f^{\left(-1\right)}\left(v\right)$inline$ отметить точки $inline$A=({v_0/2,\ f}^{-1}(v_0/2))$inline$ и $inline$B=({{2v}_0,\ f}^{-1}({2v}_0))$inline$ (рис 2), а затем соединить их отрезком, то тангенс угла наклона этого отрезка к оси $inline$Ov$inline$ будет выражаться формулой

$$display$$\frac{f^{-1}\left(2v_0\right)-f^{-1}(v_0/2)}{3/2\ \cdot\ v_0}$$display$$

то есть по сути будет равен $inline$2/3$inline$-ям от $inline$p_{success}\left(f,\ v_0\right)$inline$. То же самое наблюдение можно выразить несколько иначе: для этого нужно на отрезок $inline$AB$inline$ посмотреть как на график некоторой функции $inline$i(v)$inline$. Внутри интервала $inline$(v_0/2,\ 2v_0)$inline$ функция $inline$i(v)$inline$ имеет, очевидно, постоянную производную и $inline$p_{success}\left(f,\ v_0\right)$inline$ равен $inline$3/2$inline$-ым ее величины.

Теперь уже не сложно показать, что функция $inline$f(k)$inline$ не может превзойти $inline$l(k)=\ 2k$inline$ по величине инфинума $inline$p_{success}$inline$, иными словами, стратегия "x2" оптимальна.

Рассуждения я начну с двух предварительных замечаний:

1. $inline$f(k)\geq2k= l(k)$inline$, поэтому $inline$f^{\left(-1\right)}\left(v\right)\le l^{-1}\left(v\right)=1/2\cdot v$inline$ то есть график функции $inline$f^{\left(-1\right)}\left(v\right)$inline$ лежит не выше графика $inline$l^{-1}\left(v\right)$inline$
2. величина значения $inline$p_{success}\left(l,\ v\right)$inline$ не зависит от $inline$v$inline$ и равна $inline$3/4$inline$, производная $inline$l^{-1}\left(v\right)$inline$ во всех точках равна $inline$1/2$inline$.

Чтобы потом прийти к противоречию, сначала предположим, что $inline$f(k)$inline$ строго лучше $inline$l(k)$inline$. Последнее возможно только в том случае, если существует некоторое $inline$\varepsilon>0$inline$ и при всех $inline$v$inline$ выполняется неравенство: $inline$p_{success} (f,v)3/4 + $inline$.

Для какого-нибудь $inline$u_0>0$inline$ отметим на графике функции $inline$f^{\left(-1\right)}\left(v\right)$inline$ последовательность точек

$$display$$B_0=(u_0/2,\ f^{\left(-1\right)}\left(u_0/2\right)),\ B_1=(2u_0,\ f^{\left(-1\right)}\left(u_0\right)),\ B_2=(8u_0,\ f^{\left(-1\right)}\left(8u_0\right)),\ ...$$display$$

, соединим их ломанной $inline$B_0\ B_1B_2...B_n...$inline$ и интерпретируем эту ломанную как график кусочно-линейной функции $inline$I(v)$inline$. В последовательности $inline$u_0/2,\ 2u_0,\ 8u_0, \ldots\ $inline$ каждое последующее значение в 4 раза больше предыдущего, поэтому на каждые два идущие друг за другом числа мы можем смотреть, как на некое $inline$v_0/2$inline$ и $inline$2v_0$inline$. Последнее означает, что на каждом звене $inline$B_nB_{n+1}$inline$ ломаной $inline$I(v)$inline$ ее производная будет не меньше чем $inline$2/3\cdot{inf}_v[p_{success}\left(f,\ v\right)]2/3(3/4 +) = 1/2 + 2/3$inline$.

Поскольку производная $inline$l^{-1}\left(v\right)$inline$ равна $inline$1/2$inline$, а производная $inline$I(v)$inline$ во всех точках больше $inline$1/2$inline$ по крайней мере на $inline$2/3$inline$, то вне зависимости от значения $inline$I(v)$inline$ в точке $inline$v_0$inline$, при безграничном увеличении $inline$v$inline$ рано или поздно ее график окажется выше графика $inline$l^{-1}\left(v\right)$inline$. (рис 3)


рис 3

В то же самое время нужно вспомнить, что вершины ломаной $inline$I(v)$inline$ расположены на графике функции $inline$f^{\left(-1\right)}\left(v\right)$inline$, поэтому (смотрите замечание 1)) они сами и вся ломанная должны находится не выше графика $inline$l^{-1}\left(v\right)$inline$. Полученное противоречие как раз и доказывает, что $inline$l\left(k\right)=2k$inline$ оптимальна.

Строгие выводы: единственность
Что будет, если в только что изложенном доказательстве построить ломанную по такой последовательности вершин, которая вместо того, чтобы бесконечно удалятся от оси $inline$OK$inline$, будет наоборот к ней стремится. На самом деле этим можно доказать, что в любой вселенной, где размеры полосок фотопленки никак не ограничены снизу, кроме стратегии с функцией $inline$l\left(k\right)=2k$inline$, других оптимальных стратегий нет. Давайте в этом убедимся.

Предположим, что существует функция $inline$f\left(k\right)$inline$, которая с одной стороны оптимальна, а с другой отлична от $inline$l\left(k\right)$inline$. В таком случае функция $inline$f^{\left(-1\right)}\left(v\right)$inline$ отлична от $inline$l^{-1}\left(v\right)$inline$, а поскольку выполнятся неравенство $inline$f^{\left(-1\right)}\left(v\right)\le l^{-1}\left(v\right)$inline$, то должно найтись хотя бы одно значение $inline$v$inline$, при котором $inline$f^{\left(-1\right)}\left(v\right)$inline$ окажется строго меньше $inline$l^{\left(-1\right)}\left(v\right)$inline$. Пусть $inline$u_0$inline$ одно из таких значений $inline$v$inline$. Аналогично тому, как мы действовали выше, на графике $inline$f^{\left(-1\right)}\left(v\right)$inline$ отметим последовательность точек

$$display$$B_0=(2u_0,\ f^{\left(-1\right)}\left(2u_0\right)),\ B_1=(u_0/2,\ f^{\left(-1\right)}\left(u_0/2\right)),\ B_2=(u_0/8,\ f^{\left(-1\right)}\left(u_0/8\right)),\ ...$$display$$

и проведем через них ломанную $inline$B_0\ B_1B_2...B_n...$inline$ (рис 4). Снова будем интерпретировать эту ломанную, как некоторую кусочно-линейную функцию $inline$I(v)$inline$. Ровно по тем же причинам, что и раньше, производная функции $inline$I(v)$inline$ на каждом звене звене $inline$B_nB_{n+1}$inline$ будет не меньше чем $inline$2/3\cdot{inf}_v[p_{success}\left(f,\ v\right)]$inline$. Поскольку $inline$f$inline$ оптимальна, то $inline${inf}_v[p_{success}\left(f,\ v\right)]$inline$ должен быть не меньше, чем $inline${inf}_v[p_{success}\left(l,\ v\right)]=3/4$inline$. Объединяя два последних утверждения, мы получаем, что производная функции $inline$I(v)$inline$ нигде не меньше $inline$2/3\cdot3/4 = 1/2$inline$.


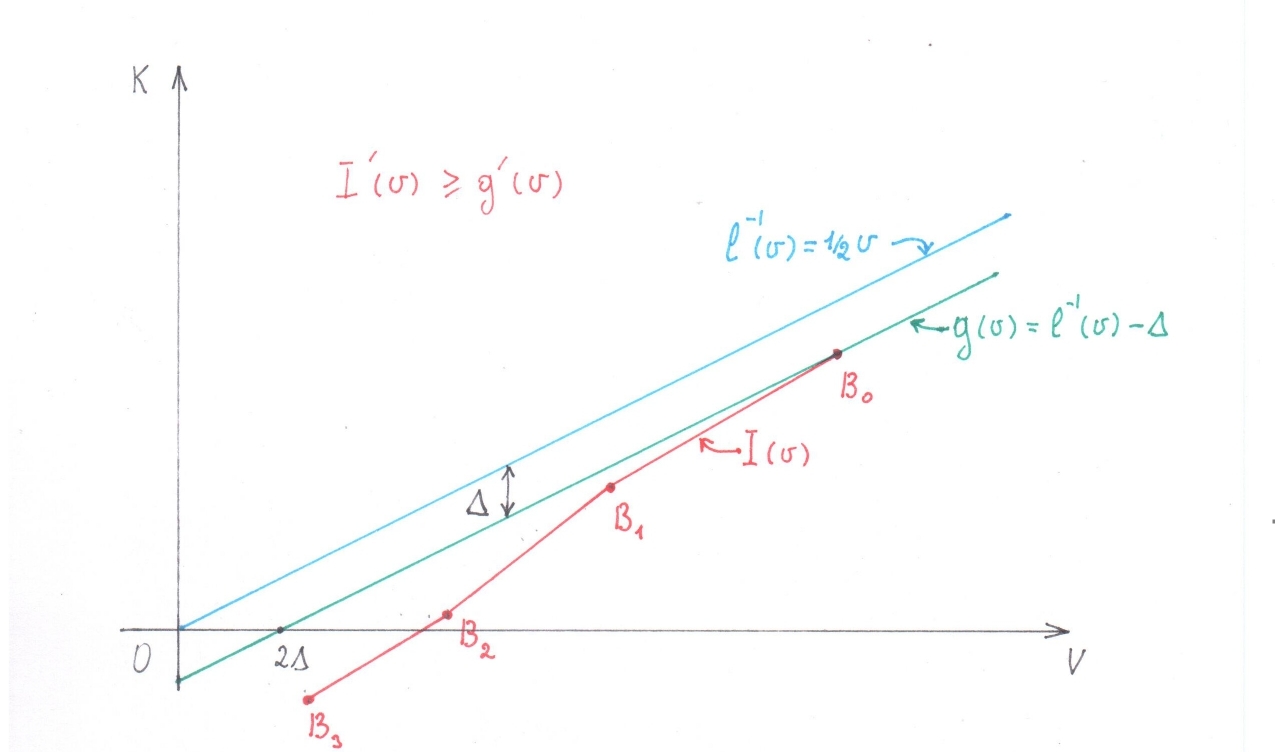
рис 4

Обозначим символ $inline$\Delta$inline$ разность $inline$l^{\left(-1\right)}\left(u_0\right)-f^{\left(-1\right)}\left(u_0\right)$inline$ и введем еще одну функцию: $inline$g(v)=l^{-1}\left(v\right) - \Delta$inline$. Среди очевидных свойств $inline$g(v)$inline$ можно отметить следующие:

1. в точке $inline$u_0$inline$ значение $inline$g(v)$inline$ совпадает со значением функции $inline$I(v)$inline$
2. производная $inline$g(v)$inline$ при всех $inline$v$inline$ одинакова и равна $inline$1/2$inline$

Давайте проследим, как будут изменятся значения функций $inline$I(v)$inline$ и $inline$g(v)$inline$ при уменьшении аргумента $inline$v$inline$ от $inline$u_0$inline$ до $inline$0$inline$. Сначала значения $inline$I(v)$inline$ и $inline$g(v)$inline$ равны. Производная $inline$I(v)$inline$ ни в одной точке промежутка $inline$(0,u_0)$inline$ не меньше производной $inline$g(v)$inline$, поэтому значения функции $inline$I(v)$inline$ убывают не медленнее, чем убывают значения $inline$g(v)$inline$. Из перечисленных фактов следует, что на всем промежутке $inline$(0,\,u_0)$inline$$inline$I(v)\le g(v)$inline$.

Поскольку $inline$g(v)=1/2\cdot v\ +\Delta$inline$, то на промежутке $inline$(0,\,2\Delta)$inline$ значения $inline$g(v)$inline$ отрицательны, а так как $inline$I(v)\le g(v)$inline$ то и значения $inline$I(v)$inline$ на нем так же должны быть отрицательными. В то же время вершины $inline$I(v)$inline$ это точки графика функции $inline$f^{\left(-1\right)}\left(v\right)$inline$, функции, которая может принимать исключительно положительные значения ($inline$f$inline$ определена только для положительных $inline$k$inline$), поэтому значения $inline$I(v)$inline$ не могут быть отрицательными. Полученное противоречие как раз и доказывает, что кроме $inline$l\left(k\right)=2k$inline$, других оптимальных оценок нет.

Дискуссионные вопросы

Постарайтесь самостоятельно приспособить решение задачи о случайной частице к условиям задачи о случайном трамвае. Какой у вас получился результат?

Представьте, что мы решаем задачу о случайной частице во вселенной, где фотопленка
не может быть короче 10 сантиметров. Покажите, что этих условиях оценка $inline$l\left(k\right)=2k$inline$ по-прежнему будет оптимальной, правда, она уже не единственная из таковых. Покажите, что оптимальной, например, является оценка $inline$l\left(k\right)=2k+10$inline$. Какие еще оптимальные оценки вам удалось найти?

К принципу максимизации гарантированного выигрыша появляется масса претензий, если заведомо известно, что ваш оппонент не имеет стремления вас обыграть. Этот принцип, например, трудно считать оправданным, когда партия игр ведется против погодных условий или против мирового рынка ценных бумаг. Какие принципы отбора стратегий в этих случаях вы бы могли предложить взамен, какие из них применимы к задаче о случайном трамвае?

Буду рад вашим мыслям и замечаниям.

Сергей Коваленко
2020 год
magnolia@bk.ru

В интересной и поучительной статье Случайный трамвай посреди незнакомого города предлагается такой эксперимент:

Представьте себе, что некто взял полоску фотографической пленки длинной N см и решил пронаблюдать за тем, как на ней будут оставлять свой след приходящие из космоса частицы. В масштабах эксперимента плотность вероятности попадания частиц на пленку будет описываться равномерным распределением на отрезке от 0 до N. В этом опыте экспериментатор сообщает вам расстояние k между левым краем пленки и точкой, куда угодила первая зарегистрированная частица. Как и прежде, от вас требуется дать приемлемую оценку для неизвестного вам N.

Для решения этой задачи было сделано такое предположение:

Представьте теперь, что в одном эксперименте расстояние от места попадания частицы до левого края фотопленки было равным Р1, а в другом эксперименте Р2, причем Р1<Р2. Не будет ли тогда разумным, длине фотопленки в первом эксперименте дать меньшую оценку, чем во втором?

Мне стало интересно в цифрах всегда ли и насколько это разумно?

Эти заметки не продолжение и не обсуждение статьи из которой взята цитата, это попытка посмотреть как сама постановка задачи, введенные ограничения, допущения и условия принимаемые на этапе формализации отразятся на полученном ответе. Я не буду приводить формулы и постараюсь не использовать специальные термины, мне кажется так будет отчетливей видна сама проблема зависимости результата от принятых или не принятых допущений.

Для начала, я изменю, упрощу и приземлю эксперимент

Судьба или наш помощник имеет мешочек в котором лежат пронумерованные по порядку бочонки, как в лото. Помощник (мне его представить легче чем судьбу) в тайне от нас достает наугад бочонок и насыпает в первый сундук пронумерованных шаров по числу на бочонке. Затем он повторяет процедуру случайного извлечения бочонка и насыпает соответствующее число пронумерованных по порядку шаров во второй сундук. Перед нами стоят два сундука с неизвестным количеством шаров в каждом из них. Мы достаем наугад один шар из первого и один шар из второго сундука, и делаем разумное предположение, что шару с большим номером соответствует сундук с большим количеством шаров.
Оценим насколько предположение разумно?

Формализуем и уточним задачу

1. Раз уж бочонки лежат в мешочке, то они должны быть ограничены каким-то числом. Помня о первоисточнике про число трамвайных линий, ограничил пока число бочонков в 30.

2. А как поступить если мы вынули из сундуков шары с одинаковыми номерами? У нас есть варианты:

2.1 признать исход неудачным, не принимать решения и попросить помощника сделать новое заполнение сундуков.

2.2 бросить монетку и наугад решить в каком сундуке шаров больше. В этом варианте не будет неудачных исходов.

2.3 решить что раз номера одинаковые, то и количество шаров в сундуках тоже одинаковое. В этом варианте тоже не будет неудачных исходов.

Тут я хочу заметить, что я не выбираю какой вариант лучше. Моя цель посмотреть как разные варианты скажутся на полученном ответе.

3. Раз у нас появилось разное количество исходов, то встает вопрос: А от какого количества исходов считать долю правильных ответов? От всех опытов или только от удачных исходов? Посчитаем оба варианта.

4. Вот вынул помощник первый бочонок, посмотрел номер, насыпал соответствующее число шаров в первый сундук. Стоп! А что он сделал с вынутым бочонком затем? У него два варианта: положить бочонок назад в мешок, а можно не класть назад в мешок. Или что тоже самое, помощник мог достать сразу два бочонка и насыпать шары в сундуки по вынутым числам на бочонках, помощники бывают ленивые, а мы не видим что он там творит. В этом случае у нас никогда не будет равное число шаров в сундуках, и следовательно неудачных исходов. Этот пункт явным образом отступает от задачи из цитаты, там бочонок возвращается назад в мешок, но у меня другие цели, да и невозвращение бочонка это типичная ситуация в жизни, посчитаем и такой вариант.

Итак, у нас есть три варианта как считать исходы опыта при которых номера шаров одинаковы, два варианта подсчета доли правильных ответов и два варианта наполнения сундуков шарами. Итого 12 вариантов результатов эксперимента!

Как вероятность правильного ответа будет зависеть от количества бочонков в мешке судьбы, то есть от максимально возможного числа шаров в сундуке? Может быть все варианты будут одинаковыми? Может быть варианты будут иметь одинаковую тенденцию? Вот в этот момент я попробовал проверить свою интуицию заполнив такую табличку:



Оказалось, забегая вперед, что тренировать и тренировать мне еще интуицию. Я подчистил табличку от многих своих соображений.

Чтобы не утомлять формулами, которые хоть и красивы, но рекуррентны, а свести рекуррентные формулы к замкнутым мне не под силу, опишу общий алгоритм расчета:

1. Для каждого числа бочонков в мешке, мы можем составить список всех вариантов наполнения сундуков шарами.

Пример: Если число бочонков 4, то получим 16 вариантов наполнения двух сундуков по количеству шаров: 1и1, 1и2, 1и3, 2и1, 2и2 4и4.

2. Для каждого варианта наполнения сундуков подсчитываем число правильных ответов для трех вариантов подсчета равных шаров.

Пример: Для наполнения сундуков 2и3, (в первом сундуке 2 шара, во втором 3) получится следующая таблица.



3. Для выбранного числа бочонков складываются все правильные ответы для каждого варианта наполнения сундуков.

4. Вычисляем долю правильных для двух вариантов подсчета (по отношению к общему числу опытов и к числу успешных).

5. Считаем так же пункты с 3 по 4 для варианта когда бочонок не возвращается в мешок, то есть когда у нас не может быть равное число шаров в сундуках.

Я подсчитал для числа бочонков с 1 до 8 и 30, чтобы была видна тенденция. Приведу графики.

Сначала для варианта когда бочонок возвращается в мешок

При увеличении числа бочонков в мешке, а следовательно увеличении возможного числа шаров в сундуках вероятность правильной оценки растет и разница между вариантами уменьшается. Любопытно, что вероятность не всегда выше 0,5. Так же любопытен желтый график, на нем есть спад и только потом подъем. Вообще, диапазон от 1 до 7 оказался не очевидным для меня.

Получается, что если шаров меньше 8, то для варианта подсчета Равные считаются неудачей. Доля правильных считается от всех опытов случайный ответ даст лучший результат чем следование правилу Больше номер шара, значит сундук содержит больше шаров.

Графики для варианта когда бочонок не возвращается в мешок и следовательно в сундуках не может быть одинаковое число шаров

Графика три, так как два совпадают, они обозначены красным цветом.

Для четырех вариантов вероятность правильного ответа падает и стремится, видимо, к 0,5!(?) Другими словами, в этих вариантах для большого числа шаров в сундуках, можно вообще не проводить опыта, а просто подбрасывать монетку результат одинаков. Собственно, вот ради этого я и решил просчитать различные варианты, я ждал каких-то неожиданностей. Я не имею строгого доказательства, что вероятность стремится именно к 0,5. Это опять моя интуиция, а она часто подводит.

Хочу еще раз подчеркнуть, что эти заметки не посвящены выбору правильной стратегии или оценке какой вариант лучше. Интерес заключался в том чтобы посмотреть влияние разных вариантов задания условий на получаемый результат.

P.S. Как и хотелось, мне удалось не использовать формул и употребить специальный термин рекуррентная формула всего один раз.

P.P.S. Если лень смотреть Википедию, то рекуррентная формула это когда вам требуется прийти в дом 30, но вы обязаны предварительно посетить все предыдущие дома с номерами от 1 до 29.

О законе больших чисел (збч) написано много (например, на английском, тут и тут, также [1]). В этом тексте я попробую рассказать о том, чем закон больших чисел не является об ошибочном восприятии этого закона и потенциальных ловушках, спрятанных в математических формулировках.

Начнем с того, что же такое закон больших чисел. Неформально, это математическая теорема о том, что вероятность отклонений среднего по выборке от математческого ожидания мала и что эта вероятность стремится к нулю при увеличении выборки. Совсем неформально, теорема утверждает, что с мы можем быть в достаточной степени уверены, что среднее по нашей выборке достаточно близко к настоящему среднему и таким образом хорошо его описывает. Разумеется, предполагается наличие традиционного статистического багажа наши наблюдения из выборки должны описывать одно и то же явление, они должны быть независимы, и мысль о том, что есть некоторое настоящее распределение с настоящим средним, не должна вызывать у нас существенных сомнений.

При формулировке закона мы говорим среднее по выборке, и все что может быть математически записано как такое среднее, попадает под действие закона. Например, доля событий в общей массе может быть записана как среднее, нам достаточно записать наличие события как 1 и отсутствие как 0. В итоге среднее будет равно частоте и частота должна быть близка к теоретическому среднему. Именно поэтому по ожидаем, что доля орлов при подрасывании идеальной монеты будет близка к .

Рассмотрим теперь ловушки и ошибочные представления об этом законе.

Во-первых, ЗБЧ не всегда верен. Это всего лишь математическая теорема с входными данными предположениями. Если предположения неверны, то и закон не обязан выполняться. Например, это так если наблюдения зависимы, или если нет уверенности в том, что настоящее среднее существует и конечно, или если изучаемое явление меняется во времени и мы не можем утверждать, что мы наблюдаем одну и ту же величину. По правде говоря, в определенной степени ЗБЧ верен и в этих случаях, например, для слабокоррелированных наблюдений или даже в том случае когда наблюдаемая величина меняется во времени. Однако, для корректного приложения этого к непосредственной реальности нужен хорошо тренированный специалист-математик.

Во-вторых, кажется верным, что ЗБЧ утверждает среднее по выборке близко к настоящему среднему. Однако, такое утверждаение остается не полным: надо обязательно добавлять с высокой долей вероятности; и эта вероятность всегда меньше 100%.

В-третьих, хочется сформулировать ЗБЧ как среднее по выборке сходится к настоящему среднему при неограниченном росте выборки. Однако, это неверно, потому что среднее по выборке вообще никуда не сходится, так как оно случайное и остается таковым для любого размера выборки. Например, даже если подбросить симметричную монету миллион раз, все равное есть шанс, что доля орлов будет далека от или даже равна нулю. В определенном смысле, всегда есть шанс получить что-то необычное. Надо признать, однако, что наша интуиция все-таки подсказыает нам что ЗБЧ должен описывать какую-то сходмость, и так есть на самом деле. Только сходится не среднее, а вероятность отклонения выборочного среднего от его истинного значения, и сходится к нулю. Так как эта идея интуитивно очень удобна (шансы увидеть что-то необычное стремятся к нулю), матетматики придумали для этого особый тип сходимости сходимость по вероятности.

В-четвертых, ЗБЧ не говорит ничего о том, когда выборочное среднее можно считать достаточно близким к теоретическому. Закон больших чисел только постулирует существование определенного явления, он ничего не говорит о том, когда его можно использовать. Получается, на ключевой вопрос с точки зрения практики могу ли я использовать ЗБЧ для моей выборки размера n?, закон больших чисел не отвечает. Ответы на эти вопросы дают другие теоремы, например, Центральная Предельная Теорема. Она дает представление о том, в каких пределах выборочное среднее может отклонятся от своего истинного значения.

В заключение следует отметить центральную роль ЗБЧ в статистике и теории вероятностей. История этого закона началась тогда, когда ученые заметили, что частоты некоторых повторяющихся явлений стабилизируются и перестают существенно менятся, при условии многократного повторения опыта или наблюдения. Поразительным было то, что эта стабилизация частот наблюдалась для совершенно несвязаных явления от бросания игральной кости до урожайности в сельском хозяйстве, указывая на возможное существование закона природы. Интересно, что этот закон природы оказался частью математики, а не физики, химии или биологии, как обычно бывает с законами природы.

[1] Illustrating the Law of Large Numbers (and Confidence Intervals) Jeffrey D Blume & Richard M Royall