Тайловость в играх очень распространенное явление, особенно в играх инди сегмента. Чаще всего используют квадратные тайлы в них проще всего задать необходимые данные, будь то карта уровня или инвентарь. Однако на квадратных и прямоугольных формах возможности подобной системы не ограничиваются.
В топовых играх конца девяностых - начала нулевых часто можно увидеть шестиугольную сетку заместо квадратной в то время это смотрелось очень интересно, в особенности в сочетании с изометрией. Именно о работе с такими сетками и пойдет речь.

Если вы не читали мою предыдущую статью про прямоугольные сетки, то рекомендую ознакомится, потому как я иногда буду опускать некоторые вещи, ссылаясь именно на нее. Дабы не изобретать велосипед, некоторые алгоритмы я взял с этой статьи на английском. Кто не хочет или не может в английский, есть ее перевод на хабре. Все демки и примеры сделаны на движке Godot Engine v 3.2.3 с использованием его встроенного языка.
Думаю в целом его синтаксис ясен, однако оставлю ссылки на некоторые функции:
-
VisualServer.canvas_item_add_line - рисование линии.
-
VisualServer.canvas_item_add_rect - рисование залитого цветом прямоугольника.
-
VisualServer.canvas_item_add_polyline - рисование множества линий между точками.
-
VisualServer.canvas_item_add_polygon - рисование залитого цветом многоугольника.
Система координат
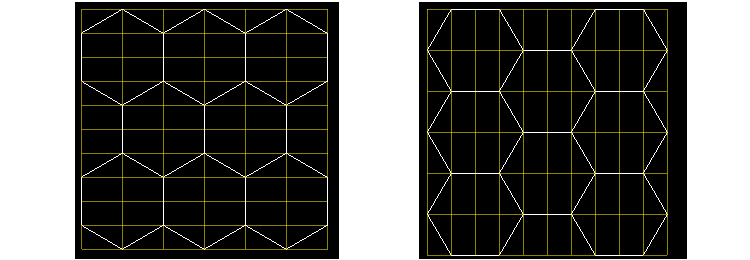
На протяжении всей статьи мы будем работать только с правильными шестиугольниками, у них все стороны равны. Работа с неправильными шестиугольниками лишена смысла в принципе. Если не брать всякие повороты и искажения, существует два вида шестиугольных сеток, вертикально и горизонтально ориентированных:
-
Такие я буду называть вертикальными (у ячейки есть явный вертикальный сосед):

-
А такие горизонтальными (у ячейки есть явный горизонтальный сосед):

Уже на этапе введения координат могут возникнуть проблемы. Дело в том, что в шестиугольной сетке невозможно ввести типичную декартову систему координат - всегда будет ось, вдоль которой у ячейки не будет явного соседа. На самом деле существует огромное количество систем координат для таких сеток. Более подробно о них рассказано в упомянутых вначале статьях. Я рассказывать про каждую не буду, все таки пост больше про использование сеток, а не их исследование.
Пожалуй первое, что приходит в голову, это таки впихнуть декартовы оси, однако для этого по одному из направлений координаты придется смещать:

Такая система называется координатами смещения. Бывает два вида координат смещения - четные и нечетные. Они отличаются лишь выбором соседа для смещения. В моем примере использованы нечетные координаты смещения, т.е. ячейка смещается к нижней в случае вертикальной ориентации или к правой в случае горизонтальной.
Главная проблема этих координат состоит в выборе базисов. Для разных ячеек базис к следующей ячейке может отличаться от того, по которому мы к ней перешли. Если вы помните из статьи про прямоугольные тайлы, там мы обращали матрицу из базисных векторов и умножали на нее радиус-вектор пикселя, получая координаты ячейки. Здесь так не выйдет, провернув тоже самое мы просто получим квадратную сетку.
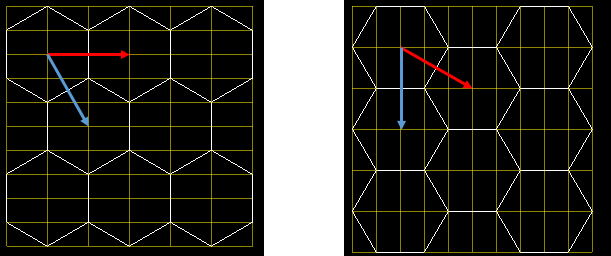
Вообще у сетки шестиугольников есть три ярко выраженных оси:

Что то напоминает, не находите? Тут три оси, прям как в пространстве. На самом деле гений тот человек - кто не просто увидел, что если взглянуть на куб под определенным углом, то получится шестиугольник, а еще и додумался использовать трехмерные координаты в двумерной сетке шестиугольников. Правда вот попробовав посчитать координаты на двумерной сетке, могут вскипеть мозги, ведь третья ось тут кажется лишней и ее использование будто только мешает. Для разрешения данной ситуации просто посмотрим откуда взялись кубы:
Для получения сетки шестиугольников надо взглянуть в изометрии на пирамидку, на каждом уменьшении высоты которой увеличивается количество кубиков в ряду на один. Включив фантазию, можно увидеть в каждом кубе шестиугольник. Включив внимательность, можно увидеть в левом нижнем углу координаты. Включив логику, можно увидеть, что сумма этих самых координат всегда равна некоторому числу, которое, кстати говоря, может быть любым, ведь мы сами решаем, откуда начнется система координат. В моем случае это 15, просто потому, что система отсчета в этом редакторе начинается с нижнего дальнего угла (в случае изометрического вида). Нам незачем таскать за собой лишнюю константу, поэтому возьмем ее за ноль. Таким образом, сумма трех координат всегда и везде равна нулю, поэтому третья нам попросту не нужна, ведь мы можем получить ее из двух других. Теперь и получается, что "мешающая" третья ось уходит. Наконец то мы можем спокойно направить базисы и у каждой ячейки всегда будет точный сосед, находящийся вдоль оси:
Т.к. у шестиугольника нет левого верхнего угла, мы можем поместить начало координат по сути в любую точку. Самым оптимальным мне показался центр фигуры, ведь относительно него она симметрична.
Преобразование координат
Пожалуй это то, на чем запарываются многие при попытке сделать нечто шестиугольное. Я слышал множество способов, порой они были очень забавные. Например, мне больше всего запомнился способ, где предлагалось сделать невидимую маску с такой же сеткой, где каждая ячейка окрашена в свой цвет, а каждому цвету соответствуют координаты. При смещении курсора смотрим в маску и по цвету определяем координаты. Сложно, с костылями, но работать может. А если мы захотим другой размер? Перерисовывать? Вы тут явно не за этим.
Вообще работать с шестиугольниками неудобно, ведь пиксели то квадратные, поэтому лучше все как то привести к прямоугольникам, что бы можно было использовать типичные матричные преобразования. Для этого найдем диагонали шестиугольника (а - сторона):

Оранжевые (маленькие) диагонали делятся пополам зелеными (большими), а зеленые оранжевыми, если последние провести из середины стороны. Уже получается, что мы можем разделить шестиугольник на 4 прямоугольника. Однако некоторые вершины в таком случае будут лежать где то между углами сетки, а ведь нам хотелось бы, чтобы все они попадали ровно в углы. На самом деле "где то", это ровно по серединке, поэтому разделим большие ячейки еще на пополам, тогда все вершины шестиугольника будут ложиться точно в углы прямоугольной сетки:
Желтую сетку в дальнейшем я буду называть вспомогательной. Для задания ее базисов будем использовать такие значения:
# Для горизонтальных шестиугольниковvar hex_size = 32var short = int(size*sqrt(3)/2) # 1/2 from short hex diagonalvar long = int(size/2) # 1/4 from long hex diagonal
Теперь мы можем выразить базисы шестиугольной сетки, используя базисы вспомогательной сетки:
Запишем все базисы в коде:
...# Transorm2D в godot - это матрица 3x2, где последняя строка указыает# смещение объекта, в дальнейшем она не будет использоваться совсем, # поэтому считайте это просто матрицей 2x2. Сделано это для удобства,# на объяснения никак не повлияет.# У нее есть два атрибута - x и y. Каждый из них это вектор. X - представляет# первый столбец матрицы 2x2 (крайняя строка не учитывается), Y - второй столбец. var grid_basis = Transform2D() # Матрица базисов вспомогательной сеткиvar hex_basis = Transform2D() # Матрица базисов гексагональной сетки... # Для вертикальной сеткиgrid_basis.x = Vector2(long, 0)grid_basis.y = Vector2(0, short)hex_basis.x = grid_basis.x*3 + grid_basis.yhex_basis.y = grid_basis.y*2# Для горизонтальной сеткиgrid_basis.x = Vector2(short, 0)grid_basis.y = Vector2(0, long)hex_basis.x = grid_basis.x*2hex_basis.y = grid_basis.x+grid_basis.y*3
Я пользуюсь именно встроенными средствами Godot для упрощения работы в целом. Все подобные места будут поясняться в общем виде, как бы это делалось без встроенных возможностей.
Шестиугольник в пиксель
Вот за что я люблю математику, так это за то, что если она работает, то работает везде. Так что для получения центра шестиугольника в пикселях из его координат на сетке надо просто умножить базисы на координаты:
func hex2pixel(hex):return hex.x*hex_basis.x + hex.y*hex_basis.y
Для получения каждой вершины просто прибавляем по нужным базисам:

Тогда для получения вершины в коде прибавляем нужный вектор (см. картинку выше) к центру шестиугольника. Я написал только функцию получения массива вершин, ибо по отдельности они почти никогда не нужны.
Для вертикальных шестиугольников:
func _get_vert_hex_vertices(hex):var pixel = hex2pixel(hex)return PoolVector2Array([pixel+2*grid_basis.x,pixel+grid_basis.x+grid_basis.y,pixel-grid_basis.x+grid_basis.y,pixel-2*grid_basis.x,pixel-grid_basis.x-grid_basis.y,pixel+grid_basis.x-grid_basis.y])
Для горизонтальных шестиугольников:
func _get_hor_hex_vertices(hex):var pixel = hex2pixel(hex)return PoolVector2Array([pixel+grid_basis.x-grid_basis.y,pixel+grid_basis.x+grid_basis.y,pixel+2*grid_basis.y,pixel-grid_basis.x+grid_basis.y,pixel-grid_basis.x-grid_basis.y,pixel-2*grid_basis.y,])
Пиксель в шестиугольник
Наверно самая интригующая часть поста. На самом деле ничего нового почти не будет, ведь для получения вещественных координат ячейки все также обращаем матрицу и умножаем на нее радиус-вектор пикселя:
Для горизонтальной ориентации
В коде это записывается так:
func pixel2hex(pixel):var x = pixel.x/(2*cw) - pixel.y/(6*ch)var y = pixel.y/(3*ch)return round_hex(Vector2(x, y))

В коде это записывается так:
func pixel2hex(pixel):var x = pixel.x/(3*cw)var y = pixel.y/(2*ch) - pixel.x/(6*cw)return round_hex(Vector2(x, y))
Однако я буду пользоваться функцией affine_inverse
у Transform2D, для того, что бы при изменении базисных
векторов постоянно не менять функции преобразований, позже увидите
зачем это надо. Вы скорее всего работаете в другой среде (и
зря), поэтому вам придется писать обращение матрицы
самостоятельно. Кто не знает как это делается, или забыл, может
почитать тут, или переписать
следующие функции в свой язык:
func invert_basis(basis:Transform2D): # обращение матрицыvar det = basis.x.x*basis.y.y - basis.y.x*basis.x.yvar idet = 1.0/det# Я не уверен что Transform2D передается по значению, по этому# копирую данные в новый объектvar res = basisres.y.y = basis.x.x*idetres.x.x = basis.y.y*idetres.x.y = -basis.x.y*idetres.y.x = -basis.y.x*idetreturn resfunc vec_mul_basis(vec:Vector2, basis:Transform2D): # умножение вектора на матрицуvar x = vec.x*basis.x.x + vec.y*basis.y.xvar y = vec.x*basis.x.y + vec.y*basis.y.yreturn Vector2(x, y)func pixel2hex(pixel):return round_hex(vec_mul_basis(pixel, invert_basis(hex_basis)))
Средствами Godot это можно записать всего в одну строчку:
func pixel2hex(pixel):return round_hex(hex_basis.affine_inverse().xform(pixel))
Тут .xform(Vector2) - это метод для умножения
матрицы на переданный в него вектор, аналог
vec_mul_basis из моего кода. Такой код работает для
обеих ориентаций.
Если вы хотя бы бегло прочитали вышеприведенный код, то
наверняка заметили функцию round_hex вместо типичных
приведений к int. Дело в том, что полных координат у
шестиугольника 3, и они обладают условием x + y + z =
0, а после округления каждой из них
равенство может нарушиться. Поэтому необходимо задать координату с
наибольшей ошибкой округления через две другие, тогда условие
выполнится. Да, данный метод полностью слизан отсюда, однако зачем
придумывать велосипед, если можно взять готовый? Так же тут
используется именно round, а не приведение к
int, ведь основание каждой ячейки находится в ее
центре, а не в левом верхнем углу, как в случае с прямоугольными
сетками:
func round_hex(hex:Vector2):var rx = round(hex.x)var ry = round(hex.y)var rz = round(-hex.x-hex.y) # z = -x-yvar x_diff = abs(hex.x-rx) # Ошибка округления xvar y_diff = abs(hex.y-ry) # Ошибка округления yvar z_diff = abs(-hex.x-hex.y-rz) # Ошибка округления zif x_diff > y_diff and x_diff > z_diff:rx = -ry-rz # Приведение под равенствоelif y_diff > z_diff:ry = -rx-rz # Приведение под равенствоreturn Vector2(rx, ry)
Работает все замечательно:
Вертикальная ориентация
Однако я надеюсь вы не думаете, что сетки, это вручную нарисованные текстуры. Я не самоубийца.
Рисование сеток
Все примеры и объяснения я буду приводить на горизонтальной сетке, ведь для вертикальной они аналогичны. Для рисования последних я просто оставлю готовую функцию.
Для рисования сетки необходимо знать ее размеры. Размеры шестиугольной сетки будем задавать в координатах смещения, так просто понятнее. Тогда по горизонтали будет в два раза больше ячеек вспомогательной сетки, чем шестиугольников, ведь по горизонтали у шестиугольника 2 ячейки. Для нахождения вертикальных размеров заметим, что для перехода к нижнему шестиугольнику мы вниз проходим три вертикальных базиса, однако для крайнего шестиугольника соседа снизу нет, поэтому самая нижняя чать остается неучтенной, так что нужно прибавить единицу:
const hex_map_size = Vector2(7, 7) # размер сетки шестиугольниковvar grid_map_size:Vector2 # размер вспомогательной сетки...grid_map_size.x = hex_map_size.x*2grid_map_size.y = hex_map_size.y*3+1
Для вертикальных шестиугольников все аналогично, только формулы для вычисления ширины и высоты меняются местами:
...grid_map_size.x = hex_map_size.x*3+1grid_map_size.y = hex_map_size.y*2
Сетку из шестиугольников можно разбить на две части, на вертикальные линии и на паттерн вершин:

Будем рисовать каждую составляющую по отдельности. Начнем с
вертикальных линий. Можно заметить, что в каждом ряду линии
рисуются с интервалом в 2 ячейки, а каждый четный по счету ряд
начинается со второй, а не с первой ячейки. Также увидим то, что
первый ряд начинается со со смещением в одну ячейку относительно
верхей границы, а ряды разделяет одна ячейка. С учетом того, что
длина штриха в две ячейки, между верхними концами отрезков
находятся три ячейки. Тогда в цикле начинаем с единицы и идем до
нижнего края карты с шагом 3, а во втором цикле начинаем со
столбца, индекс которого обратен четности ряда, проще говоря
1-i%2, и идем до правого края карты, но на единицу
больше, чтобы нарисовать таки крайние линии, с шагом в две ячейки.
В кадой итерации второго цикла просто рисуем отрезок высотой две
ячейки:
for i in range(1, grid_map_size.y, 3):for j in range(1-i%2, grid_map_size.x+1, 2):VisualServer.canvas_item_add_line(surf, grid_basis.x*j+grid_basis.y*i, grid_basis.x*j+grid_basis.y*(i+2), color, width, antialiasing)
Этот код будет рисовать только вертикальные линии. Теперь нужно нарисовать паттерн вершин. Есть всего два вида наклонных линий, от нижнего левого угла к верхнему правому (их я буду называть нижними диагоналями), или от верхнего левого к нижнему правому (их я буду называть верхними диагоналями), причем в одной строке они чередуются, а в следующей строке паттерн меняет четность. Четным я буду называть паттерн, начинающийся с нижней диагонали, нечетным - начинающийся в верхней диагонали.
Каждые две строки паттерна разделяют две ячейки, поэтому чтобы перейти от одной к следующей, необходимо сдвинуться на 3 строки вниз. Как я уже говорил, каждую строку паттерн меняет четность, и так совпало, что при переходе к следующей строке ее индекс тоже меняет четность.
Для рисования паттернов пробегаем каждую третью строку, начиная
с нулевой, а в каждой строке пробегаемся по столбцам. Тогда для
выбора нужной линии сравниваем четности строки и столбца, если они
совпадают, то рисуем нижнюю диагональ, иначе верхнюю. Тут я считаю
нужным показать, как задается каждый угол ячейки с координатами
{j, i} , где j - столбец (как бы
x), i - строка (как бы y).
Размер ячейки увеличен только для демонстрации:

В коде этот алгоритм выглядит так:
# Drawing verticesfor i in range(0, grid_map_size.y, 3): # рисуем на каждой третьей строкеfor j in range(grid_map_size.x): # крайний столбец не захватываем, т.к. в коде прибавляется единицаif i%2 == j%2: # нижняя диагональCanvas.line(surf, grid_basis.x*j+grid_basis.y*(i+1), grid_basis.x*(j+1)+grid_basis.y*i, color, width, antialiasing)else: # верхняя диагональCanvas.line(surf, grid_basis.x*j+grid_basis.y*i-offset, grid_basis.x*(j+1)+grid_basis.y*(i+1), color, width, antialiasing)
Однако просто нарисовав на холсте сетку, получатся непонятки с координатами:

Дело все в том, что начало координат находится в центре шестиугольника, а начинаем рисовать мы с левого верхнего угла вспомогательной сетки, также как мы это делали с обычными сетками. Для рисования сетки правильно, т.е. из начала координат, необходимо сдвинуть рисование на одну ячейку влево и на две вверх, ведь именно под таким смещением находится начало координат.
Однако и на этом не все. Если просто объеденить весь код выше в одну функцию, то при четных высотах она будет рисовать ненужные хвосты:

Эти хвосты рисуются прямо в углах вспомогательной сетки, поэтому просто добавим уловие, что мы в них не находимся, иначе просто не рисуем тут диагональ.
Соеденив все вместе, получим такую функцию:
func _draw_hor_rect_grid(surf:RID, color:Color, width=1.0, antialiasing=false):var offset = grid_basis.x+grid_basis.y*2# Drawing vertical linesfor i in range(1, grid_map_size.y, 3):for j in range(1-i%2, grid_map_size.x+1, 2):VisualServer.canvas_item_add_line(surf, grid_basis.x*j+grid_basis.y*i-offset, grid_basis.x*j+grid_basis.y*(i+2)-offset, color, width, antialiasing)# Drawing verticesfor i in range(0, grid_map_size.y, 3):for j in range(grid_map_size.x):if int(hex_map_size.y)%2 == 1 or not (i == grid_map_size.y-1 and (j == 0 or j == grid_map_size.x-1)):if i%2 == j%2:VisualServer.canvas_item_add_line(surf, grid_basis.x*j+grid_basis.y*(i+1)-offset, grid_basis.x*(j+1)+grid_basis.y*i-offset, color, width, antialiasing)else:VisualServer.canvas_item_add_line(surf, grid_basis.x*j+grid_basis.y*i-offset, grid_basis.x*(j+1)+grid_basis.y*(i+1)-offset, color, width, antialiasing)
При рисовании вспомогательной сетки кстати тоже используем смещение. На всякий случай оставлю тут и ее рисование, хотя это есть в моей статье про прямоугольные сетки:
func draw_auxiliary_grid(surf:RID, color:Color, width=1.0, antialiasing=false):var offset = grid_basis.x+grid_basis.y*2for i in grid_map_size.x+1:Canvas.line(surf, grid_basis.x*i-offset, grid_basis.x*i+grid_basis.y*grid_map_size.y-offset, color, width, antialiasing)for i in grid_map_size.y+1:Canvas.line(surf, grid_basis.y*i-offset, grid_basis.x*grid_map_size.x+grid_basis.y*i-offset, color, width, antialiasing)
И, как и обещал, функция для рисования вертикально-ориентированной сетки:
func _draw_vert_rect_grid(surf:RID, color:Color, width=1.0, antialiasing=false):var offset = grid_basis.x*2+grid_basis.y# Drawing horizontal linesfor i in range(1, grid_map_size.x, 3):for j in range(1-i%2, grid_map_size.y+1, 2):VisualServer.canvas_item_add_line(surf, grid_basis.x*i+grid_basis.y*j-offset, grid_basis.x*(i+2)+grid_basis.y*j-offset, color, width, antialiasing)# Drawing verticesfor i in range(0, grid_map_size.x, 3):for j in range(grid_map_size.y):if int(hex_map_size.x)%2 == 1 or not(i == grid_map_size.x-1 and (j == 0 or j == grid_map_size.y-1)):if j%2 == i%2:VisualServer.canvas_item_add_line(surf, grid_basis.x*(i+1)+grid_basis.y*j-offset, grid_basis.x*i+grid_basis.y*(j+1)-offset, color, width, antialiasing)else:VisualServer.canvas_item_add_line(surf, grid_basis.x*i+grid_basis.y*j-offset, grid_basis.x*(i+1)+grid_basis.y*(j+1)-offset, color, width, antialiasing)
Результат вполне неплох, нигде линии не рисуются дважды (сетка рисовалась немного прозрачной на черном фоне, а яркость линий везде одинакова):
Сетка вертикальных шестиугольников

Однако рендерить такие сетки в реальном времени довольно
затратно, тут рисуется множетсво отдельных отрезков, что сильно
замедляет работу. Просто для примера, пустое черно окно у меня
имеет fps около 950, а при рисовании белым цветом
Color8(255, 255, 255, 200) шестиугольной сетки размера
10x10 и размером шестиугольнкиа 32 пикселя, fps
примерно 260. Так что рисовать сетки процедурно резонно только на
начальном этапе разработки, потом лучше отрендерить ее заранее и
использовать как текстуру.
Рисование шестиугольной сетки шестиугольников
Сетки шестиугольников конечно здорово, но иногда хочется чего то большего. Например больше шестиугольников, поэтому сделаем большой шестиугольник из маленьких. Такая сетка может пригодиться, если мы, например, делаем шестиугольные шахматы.
Рисование этой сетки лишь немного сложнее рисования обычной, хотя на первый взгляд мой код похож на код сатаны. Поробую объяснить что откуда взялось. Результат будет примерно таков:

Для начала нам конечно же нужны размеры сеток. Т.к. мы рисуем
сетку в виде правильного шестиугольника, ее размер можно задать
одним значением. В коде я использую тип Vector2 только
для совмещения этой переменной с прямоугольнйо сеткой, при
рисовании будет использоваться только X координата.
Тогда для задания размеров вспомогательной сетки нужно найти
диагональ большого шестиугольника. Для этого вспомним, что бОльшая
диагональ шестиугольника в два раза больше его стороны. В нашем
случае шестиугольник состоит из маленьких таких же. В таком случае
центр будет учитываться два раза, поэтому вычтем единицу:
var hex_map_size = Vector2(5, <не имеет значения>)...var diagonal = hex_map_size.x*2-1
Размеры вспомогательной сетки задаются аналогично тому, что мы делали ранее. Для горизонтальной ориентации ширина будет в два раза больше диагонали, а высота в три раза и еще на единицу больше:
...grid_map_size.x = diagonal*2grid_map_size.y = diagonal*3+1
Для вертикальных значения меняются местами:
grid_map_size.x = diagonal*3+1grid_map_size.y = diagonal*2
Шестиугольную сетку можно точно также разбить на две части, на паттерн вершин и вертикальные линии:

Начнем с рисования вершин. Рисовать каждый слой по-отдельности
не имеет смысла, ведь фигура симметрична. Мы можем разделить всю
вспомогательную сетку на четыре части и, нарисовав одну четверть,
отобразить ее зеркально на все остальные. Сетка кстати всегда будет
делиться ровно, и вот почему. По горизонтали понятно, ведь в
формуле ширины мы удваиваем диагональ шестиугольной карты. А эта
самая диагональ будет всегда нечетна, ведь мы от четного числа
отнимаем единицу (hex_map_size.x*2-1). В формуле
высоты вспомогательной сетки мы умножаем эту диагональ на
3, и результат получится тоже нечетным, а после
прибавления единицы все выражение становится четным. Таким образом
ширина и высота вспомогательной сетки всегда четны, и как
следствие, ее можно всегда разделить на четыре одинаковые
части:

Тогда мы можем пробегать в циклах только до половин размеров вспомогательной сетки, а для рисования в других частях будем просто отражать точки рисования.
При такой форме сетки рисование вершин начинается не с самой левой колонки и паттерн всегда четный (при рассмотрении одной четверти). При увеличении размера сетки на единицу, первый шестиугольник в самом верхем ряду сдвигается на одну ячейку вспомогательной сетки, т.к. мы увеличиваем в том числе и размер левой грани, в которой под каждым шестиугольником следующий находится не только ниже, но и левее на половину шестиугольника, т.е. на одну ячейку. Тогда каждый следующий паттерн начинает рисоватся на ячейку ближе к левому краю, а самый первый ряд имеет смещение на единицу меньшее, чем размер шестиугольной карты, т.к. первый шестиугольник в нем тоже является частью левой грани, так что под ним шестиугольников меньше на эту самую единицу, чем размер карты.
Также вспомним, что каждый следующий паттерн рисуется со смещением в три ячейки от предыдущего, поэтому в цикле идем от нуля до половины высоты вспомогательной сетки с шагом в три, попутно вычисляя смещение для каждого ряда:
for i in range(0, grid_map_size.y/2, 3): # Drawing vertices # тут i/3 потому что мы идем со смещением 3, а при расчетах нужен индекс start = hex_map_size.x-1 - i/3
Проходить по ширине будем также до середины вспомогательной сетки, начиная с выщитанного ранее смщения:
for i in range(0, grid_map_size.y/2, 3): # Drawing vertices # тут i/3 потому что мы идем со смещением 3, у при расчетах нужен индекс паттерна start = hex_map_size.x-1 - i/3 for j in range(start, grid_map_size.x/2): pass # Пока ничего не делаем
Каждый паттерн при рисовании шестиугольной карты четный, а вот смещение чередует свою четность. Четность начального смещения напрямую зависит от четности размера карты - они противоположны. Двигаясь вниз по рядам паттерна, индекс ряда меняет четность, как и смещение для этого ряда. Если помните, для выбора диагонали при рисовании прямоугольной сетки мы сравнивали четность ряда и колонки. Тут же меняются обе четности, и при разных раземрах карты они будут то совпадать при начальных значениях, то нет.
Приведу пример. Мы рисуем нижнюю диагональ, если индексы ряда и
колонки совпадают, иначе верхнюю. Поставим размер карты 5. Тогда
начальное смещение будет четным, как и индекс первого ряда
(i=0). Исходя из условия, рисуем нижнюю диагональ, как
и должно быть. Однако поставив четный размер, скажем, 4, начальное
смещение будет нечетным, а вот индекс первого ряда по прежнему
четным. Тогда взглянув на условие компьютер выберет верхюю
диагональ, а ведь нам все еще для начала нужна нижняя. Вот как это
будет выглядеть:

Тут на самом деле всего лишь надо поменять четность паттерна,
тогда все встанет на свои места. Получается, выбор условия рисвания
нижней диагонали зависит от четности самого размера карты. Тут
можно заметить, что разница четностей столбца и ряда в каждой
первой диагонали ряда паттерна обратна четности размера карты. А
при рисовании паттерна диагонали просто чередуются, как и
чередуется четность столбца, и как следствие чередуется равенство
разностей четностей ряда и столбца и четности размера карты.
Поэтому для выбора диагонали используем равентво abs(i%2 -
j%2) != parity, где parity - это остаток от
деления размера карты на два. Если это условие верно, рисуем нижнюю
диагональ, иначе верхнюю. Получим то что нужно, осталось отразить
по красным линиям:
 Код рисования четверти всего паттерна
Код рисования четверти всего паттерна
func _draw_hor_hex_grid(surf:RID, color:Color):var parity = int(hex_map_size.x)%2var startfor i in range(0, grid_map_size.y/2, 3): # Drawing verticesstart = hex_map_size.x - i/3 - 1for j in range(start, grid_map_size.x/2):if abs(i%2 - j%2) != parity:# Down diagonalVisualServer.canvas_item_add_line(surf, grid_basis.x*j+grid_basis.y*(i+1), grid_basis.x*(j+1)+grid_basis.y*i, color) else:# Top diagonalVisualServer.canvas_item_add_line(surf, grid_basis.x*(j)+grid_basis.y*(i), grid_basis.x*(j+1)+grid_basis.y*(i+1), color)
Для отражения точек рисования отнимаем от края вспомогательной сетки индекс точки, ничего сложного. А вот в коде это выглядит громоздко. Взгляните сами:
func _draw_hor_hex_grid(surf:RID, color:Color, width=1.0, antialiasing=false):var parity = int(hex_map_size.x)%2var startfor i in range(0, grid_map_size.y/2, 3): # Drawing verticesstart = hex_map_size.x - i/3 - 1for j in range(start, grid_map_size.x/2):if abs(i%2 - j%2) != parity:# Down diagonalVisualServer.canvas_item_add_line(surf, grid_basis.x*j+grid_basis.y*(i+1), grid_basis.x*(j+1)+grid_basis.y*i, color)VisualServer.canvas_item_add_line(surf, grid_basis.x*(grid_map_size.x-j)+grid_basis.y*(i+1), grid_basis.x*(grid_map_size.x-j-1)+grid_basis.y*i, color)VisualServer.canvas_item_add_line(surf, grid_basis.x*j+grid_basis.y*(grid_map_size.y-i-1), grid_basis.x*(j+1)+grid_basis.y*(grid_map_size.y-i), color)VisualServer.canvas_item_add_line(surf, grid_basis.x*(grid_map_size.x-j)+grid_basis.y*(grid_map_size.y-i-1), grid_basis.x*(grid_map_size.x-j-1)+grid_basis.y*(grid_map_size.y-i), color)else:# Top diagonalVisualServer.canvas_item_add_line(surf, grid_basis.x*(j)+grid_basis.y*(i), grid_basis.x*(j+1)+grid_basis.y*(i+1), color)VisualServer.canvas_item_add_line(surf, grid_basis.x*(grid_map_size.x-j)+grid_basis.y*(i), grid_basis.x*(grid_map_size.x-j-1)+grid_basis.y*(i+1), color)VisualServer.canvas_item_add_line(surf, grid_basis.x*(j)+grid_basis.y*(grid_map_size.y-i), grid_basis.x*(j+1)+grid_basis.y*(grid_map_size.y-i-1), color)VisualServer.ca
Но ничего страшного, ковид пережили - переживем и это. Зато получаем правильный паттерн для сеток с четными и нечетным размером:

Если вы что то поняли во всей этой мешанине четностей, то либо вы гений, либо у меня получилось что то объяснить. Однако дальше не легче, но радует то, что мы почти нарисовали сетку. Осталось добавить вертикальные линии - это будет финальным боссом в рассказе о рисовании сеток.
Тут я не стал ничего придумывать с отражениями, ведь отрезки рисуются в две ячейки и при отражении некоторые места будут рисоваться два раза, а обрабатывать кучу исключений отдельно не очень хочется. Самым простым решение мне показалось рисовать вертикальные линии также, как мы это делали с прямоугольной сеткой, только отбрасывать линии в углах. Напомню код рисования линий в простой прямоугольной сетке:
for i in range(1, grid_map_size.y, 3):for j in range(1-i%2, grid_map_size.x+1, 2):VisualServer.canvas_item_add_line(surf, grid_basis.x*j+grid_basis.y*i, grid_basis.x*j+grid_basis.y*(i+2), color, width, antialiasing)
Однако просто скопипастив его в нашу функцию, получим кривое
рисование при четных размерах карты, ведь при них первый ряд должен
иметь смещение в единицу, а при нечетных этого смещения быть не
должно. Это вытекает из смещения первого шестиугольника в первом
ряду, при четных значения оно нечетно поэтому и рисуем со
смещением, и наоборот. Для выбора смещения сравним четности размера
карты и ряда, если они отличаются, то рисуем без смещения, иначе со
смещением. Пихать сюда условие не имеет смысла, ведь мы можем
выбрать смещение через отличие четности карты и четности столбца
конструкцией abs(parity-i%2). Просто напомню -
parity это остаток от деления размера карты на два.
Проверьте сами, при четных столбцах и нечетных размерах карты
получается единица - то самое смещение. Запишем это выражение в
смещение в цикле:
for i in range(1, grid_map_size.y, 3):for j in range(abs(parity-i%2), grid_map_size.x+1, 2):VisualServer.canvas_item_add_line(surf, grid_basis.x*j+grid_basis.y*i, grid_basis.x*j+grid_basis.y*(i+2), color, width, antialiasing)
Цель почти достигнута, осталось избавиться от лишних линий по углам:

Для этого при рисовании линий добавим некоторое условие, что мы хотим нарисовать линию в пределах каких-то границ. Для обозначения границ заметим, что с каждым рядом мы начинаем рисовать на ячейку ближе к левой границе, поэтому границу можно задать как смещение первого ряда минус индекс ряда:
...start = hex_map_size.x-1 - i/3
Однако в нижней половине шестиугольника смещение начинает идти обратно, а индекс ряда только возрастает. Поэтому будем смотерть, в какой половине мы находимся, и выбирать нужную формулу для расчета левой границы. Для нижней части карты используем положение ряда относительно центра карты, просто отняв от его индекса половину ее размера:
...start = (i-grid_map_size.y/2)/3
Это мы задали левые границы. Для правых просто отразим левые в силу четности размеров вспомогательной сетки:
for i in range(1, grid_map_size.y, 3):if i <= grid_map_size.y/2:start = hex_map_size.x-1 - i/3else:start = (i-grid_map_size.y/2)/3for j in range(abs(parity-i%2), grid_map_size.x+1, 2):if j >= start and j <= grid_map_size.x-start: # избавляемся от лишних линийVisualServer.canvas_item_add_line(surf, grid_basis.x*j+grid_basis.y*i, grid_basis.x*j+grid_basis.y*(i+2), color, width, antialiasing)
Вот и все - финальный босс побежден. Осталось только добавить
смещение для расположения сетки в начало координат, offset =
grid_basis.x+grid_basis.y*2. Однако тут опять играет роль
четность размера карты, так что когда она четна прибавляем к
смещению горизонтальный базис ячейки.
Босса то убили, а вот лут забыли. С него мы получили рисование шестиугольных сеток шестиугольников:
Горизонтальная ориентация
func _draw_hor_hex_grid(surf:RID, color:Color, width=1.0, antialiasing=false):var parity = int(hex_map_size.x)%2var offset = grid_basis.x+grid_basis.y*2 + grid_basis.x*(1-parity)var startfor i in range(0, grid_map_size.y/2, 3): # Drawing verticesstart = hex_map_size.x - i/3 - 1for j in range(start, grid_map_size.x/2):if abs(i%2 - j%2) != parity:# Down diagonalVisualServer.canvas_item_add_line(surf, grid_basis.x*j+grid_basis.y*(i+1)-offset, grid_basis.x*(j+1)+grid_basis.y*i-offset, color)VisualServer.canvas_item_add_line(surf, grid_basis.x*(grid_map_size.x-j)+grid_basis.y*(i+1)-offset, grid_basis.x*(grid_map_size.x-j-1)+grid_basis.y*i-offset, color)VisualServer.canvas_item_add_line(surf, grid_basis.x*j+grid_basis.y*(grid_map_size.y-i-1)-offset, grid_basis.x*(j+1)+grid_basis.y*(grid_map_size.y-i)-offset, color)VisualServer.canvas_item_add_line(surf, grid_basis.x*(grid_map_size.x-j)+grid_basis.y*(grid_map_size.y-i-1)-offset, grid_basis.x*(grid_map_size.x-j-1)+grid_basis.y*(grid_map_size.y-i)-offset, color)else:# Top diagonalVisualServer.canvas_item_add_line(surf, grid_basis.x*(j)+grid_basis.y*(i)-offset, grid_basis.x*(j+1)+grid_basis.y*(i+1)-offset, color)VisualServer.canvas_item_add_line(surf, grid_basis.x*(grid_map_size.x-j)+grid_basis.y*(i)-offset, grid_basis.x*(grid_map_size.x-j-1)+grid_basis.y*(i+1)-offset, color)VisualServer.canvas_item_add_line(surf, grid_basis.x*(j)+grid_basis.y*(grid_map_size.y-i)-offset, grid_basis.x*(j+1)+grid_basis.y*(grid_map_size.y-i-1)-offset, color)VisualServer.canvas_item_add_line(surf, grid_basis.x*(grid_map_size.x-j)+grid_basis.y*(grid_map_size.y-i)-offset, grid_basis.x*(grid_map_size.x-j-1)+grid_basis.y*(grid_map_size.y-i-1)-offset, color)for i in range(1, grid_map_size.y, 3):if i <= grid_map_size.y/2:start = hex_map_size.x-1 - i/3else:start = (i-grid_map_size.y/2)/3for j in range(abs(parity-i%2), grid_map_size.x+1, 2):if j >= start and j <= grid_map_size.x-start:VisualServer.canvas_item_add_line(surf, grid_basis.x*j+grid_basis.y*i-offset, grid_basis.x*j+grid_basis.y*(i+2)-offset, color, width, antialiasing)
Пример:

func _draw_vert_hex_grid(surf:RID, color:Color, width=1.0, antialiasing=false):var parity = int(hex_map_size.x)%2var offset = grid_basis.x*2+grid_basis.y + (1-parity)*grid_basis.yvar startfor j in range(0, grid_map_size.x/2, 3): # Drawing verticesstart = hex_map_size.x - j/3 - 1for i in range(start, grid_map_size.y/2):if abs(i%2 - j%2) != parity:# Down diagonalVisualServer.canvas_item_add_line(surf, grid_basis.x*(j+1)+grid_basis.y*(i)-offset, grid_basis.x*(j)+grid_basis.y*(i+1)-offset, color)VisualServer.canvas_item_add_line(surf, grid_basis.x*(grid_map_size.x-j-1)+grid_basis.y*(i)-offset, grid_basis.x*(grid_map_size.x-j)+grid_basis.y*(i+1)-offset, color)VisualServer.canvas_item_add_line(surf, grid_basis.x*(j+1)+grid_basis.y*(grid_map_size.y-i)-offset, grid_basis.x*(j)+grid_basis.y*(grid_map_size.y-i-1)-offset, color)VisualServer.canvas_item_add_line(surf, grid_basis.x*(grid_map_size.x-j-1)+grid_basis.y*(grid_map_size.y-i)-offset, grid_basis.x*(grid_map_size.x-j)+grid_basis.y*(grid_map_size.y-i-1)-offset, color)else:# Top diagonalVisualServer.canvas_item_add_line(surf, grid_basis.x*(j)+grid_basis.y*(i)-offset, grid_basis.x*(j+1)+grid_basis.y*(i+1)-offset, color)VisualServer.canvas_item_add_line(surf, grid_basis.x*(grid_map_size.x-j)+grid_basis.y*(i)-offset, grid_basis.x*(grid_map_size.x-j-1)+grid_basis.y*(i+1)-offset, color)VisualServer.canvas_item_add_line(surf, grid_basis.x*(j)+grid_basis.y*(grid_map_size.y-i)-offset, grid_basis.x*(j+1)+grid_basis.y*(grid_map_size.y-i-1)-offset, color)VisualServer.canvas_item_add_line(surf, grid_basis.x*(grid_map_size.x-j)+grid_basis.y*(grid_map_size.y-i)-offset, grid_basis.x*(grid_map_size.x-j-1)+grid_basis.y*(grid_map_size.y-i-1)-offset, color)for i in range(1, grid_map_size.x, 3):if i <= grid_map_size.x/2:start = hex_map_size.x-1 - i/3else:start = (i-grid_map_size.x/2)/3for j in range(abs(parity-i%2), grid_map_size.y+1, 2):if j >= start and j <= grid_map_size.y-start:VisualServer.canvas_item_add_line(surf, grid_basis.x*i+grid_basis.y*j-offset, grid_basis.x*(i+2)+grid_basis.y*(j)-offset, color, width, antialiasing)
Пример:

Рисование шестиугольников
Тут на самом деле все просто, можете расслабиться. После этой жести с четностями ничего хуже уже не будет. Для рисования шестиугольников вспомним функции для получения вершин, которые я приводил выше и просто соеденим массив вершин шестиугольника линиями:
Функции для получения вершин, если лень мотать неаверх
func _get_vert_hex_vertices(hex):var pixel = hex2pixel(hex)return PoolVector2Array([pixel+2*grid_basis.x,pixel+grid_basis.x+grid_basis.y,pixel-grid_basis.x+grid_basis.y,pixel-2*grid_basis.x,pixel-grid_basis.x-grid_basis.y,pixel+grid_basis.x-grid_basis.y])func _get_hor_hex_vertices(hex):var pixel = hex2pixel(hex)return PoolVector2Array([pixel+grid_basis.x-grid_basis.y,pixel+grid_basis.x+grid_basis.y,pixel+2*grid_basis.y,pixel-grid_basis.x+grid_basis.y,pixel-grid_basis.x-grid_basis.y,pixel-2*grid_basis.y,])
И рисуем множество линий между точками, не забыв замкнуть цепь:
func _draw_hor_hex(hex, surf, color, width=1.0, antialiasing=false):var points = _get_hor_hex_vertices(hex)points.append(points[0]) # замыкаемVisualServer.canvas_item_add_polyline(surf, points, [color], width, antialiasing)func _draw_vert_hex(hex, surf, color, width=1.0, antialiasing=false):var points = _get_vert_hex_vertices(hex)points.append(points[0]) # замыкаемVisualServer.canvas_item_add_polyline(surf, points, [color], width, antialiasing)
Для заливки шестиугольника, по аналогии с прямоугольником, рисуем полигон:
func _fill_hor_hex(hex, surf, color, antialiasing=false):var points = _get_hor_hex_vertices(hex)VisualServer.canvas_item_add_polygon(surf, points, [color], [], RID(), RID(), antialiasing)func _fill_vert_hex(hex, surf, color, antialiasing=false):var points = _get_vert_hex_vertices(hex)VisualServer.canvas_item_add_polygon(surf, points, [color], [], RID(), RID(), antialiasing)
Выгялдит все это как то так:

Шестиугольные сетки в изометрии
Что может быть лучше сетки шестиугольников? Правильно, сетка шестиугольников в изометрии. Вы могли заметить, что ни в одной функции я не использовал числа - везде я работал с векторами. А это значит, что поменяв базис, автоматически поменяются функции - так и должно работать программирование. Помните, в части про преобразование координат я все вычисления автоматизировал? Так вот, наконец то нам это пригодится.
Как вы уже наверняка поняли, шестиугольная сетка это лишь обертка над обычной прямоугольной, ведь все функции рано или поздно сходятся к работе с базисами вспомогательной сетки. Поэтому для создания изометрии не будем придумывать велосипед, просто зададим ее переменной, отвечающей за искажение отношений горизонтальных размеров к вертикальным:
...const iso_scale = 2.0
Тогда для изменения вида делим y-координату каждого
базиса вспомогательной сетки на это искажение:
# Вертикальная ориентацияgrid_basis.x = Vector2(long, 0)grid_basis.y = Vector2(0, short/iso_scale)# Горизонтальная ориентацияgrid_basis.x = Vector2(short, 0)grid_basis.y = Vector2(0, long/iso_scale)
И все, даже не нужно менять базисы шестиугольной сетки, ведь мы их задавали через базисы вспомогательной. Как же хороша эта ваша математика... Вот пример:

На самом деле, благодаря векторным преобразованиям мы можем делать с базисами вспомогательной сетки все что угодно, и все функции все равно будут работать. Поэтому давайте сделаем сетку не просто в изометрии, а еще и повернем ее на 45, также, как мы это делали в статье про прямоугольные сетки:
# для вертикальныхvar pw = int(long*cos(PI/4))var ph = int(short*cos(PI/4))grid_basis.x = Vector2(pw, pw/iso_scale)grid_basis.y = Vector2(-ph, ph/iso_scale)# для горизонтальныхvar pw = int(short*cos(PI/4))var ph = int(long*cos(PI/4))grid_basis.x = Vector2(pw, pw/iso_scale)grid_basis.y = Vector2(-ph, ph/iso_scale)
Напомню, что базисы шестиугольной сетки мы не трогаем, ведь они все так же заданы через базисы вспомогательной. Выглядит вся эта магия как то так:

Красиво, конечно, но игру на этом не сделать. Нужно также уметь что то на этих сетках делать.
Изометрические преобразования
С преобразованиями тоже мудрить ничего не стоит, ведь, напомню, шестиугольная сетка - это только обертка над обычной, поэтому все функции будут работать в штатном режиме. Единственное, что наверно стоит рассмотреть, это получение ячейки вспомогательной сетки, левый верхний угол которой находится в центре шестиугольника.
Для этого вспомним то, как мы направляли базисы для различных ориентаций шестиугольников. Вот картинка из почти самого начала моего рассказа:

Посмотрев на нее, все сразу становится ясно. В случае
горизонтальной ориентации при каждом перемещении по x
на шестигольной сетке мы двигаемся на две ячейки вспомогательной, а
при движении по y мы движемся на одну ячейку вправо и
на три вниз. Для вертикальных применима эта же логика. По этим
формулам написать функции можно проще простого:
# Для вертикальныхfunc get_center_cell(hex:Vector2):return Vector2(hex.x*3, hex.y*2+hex.x)# для горизонтальныхfunc get_center_cell(hex:Vector2):return Vector2(hex.x*2+hex.y, hex.y*3)
В изометрии ближние объекты должны рисоваться раньше дальних, и, если помните, в пямоугольных изометрических сетках мы использовали сумму координат. Здесь делаем тоже самое, только находим сумму координат центральной ячейки в шестиугольнике, получаемую по алгоритму выше.
Расстояние на сетке
Часто бывает нужно найти расстояние между двумя шестиугольниками. Для этого заметим, что при перемещении в любой из соседних шестиугольников меняются сразу две координаты из трех, причем не единицу. Тогда сумма модулей всех трех координат либо меняется на два, либо не изменятся вовсе. В таком случае сеточное расстояние от начала координат можно найти как половину суммы модулей трех координат шетиугольника, а для нахождения расстояния между двумя шестиугольниками можно просто найти смещение одного относительно другого через разность. Получается вот такая небольшая функция:
func hex_distance(hex1:Vector2, hex2:Vector2):var dif = (hex2-hex1)return (abs(dif.x) + abs(dif.y) + abs(-dif.x-dif.y))/2 # z = -x-y
Сеточное направление
Начнем с самого простого - выбора направляющего шестиугольника. Кто не понимает о чем речь, заглянет в статью о прямоугольных тайловых мирах. Это один из немногих алгоритмов, где нам понадобится третья координата.
Для нахождения направляющей разделим сетку по трем осям и заметим, что в каждой части получившейся сетки одна из трех координат максимальна по модулю:
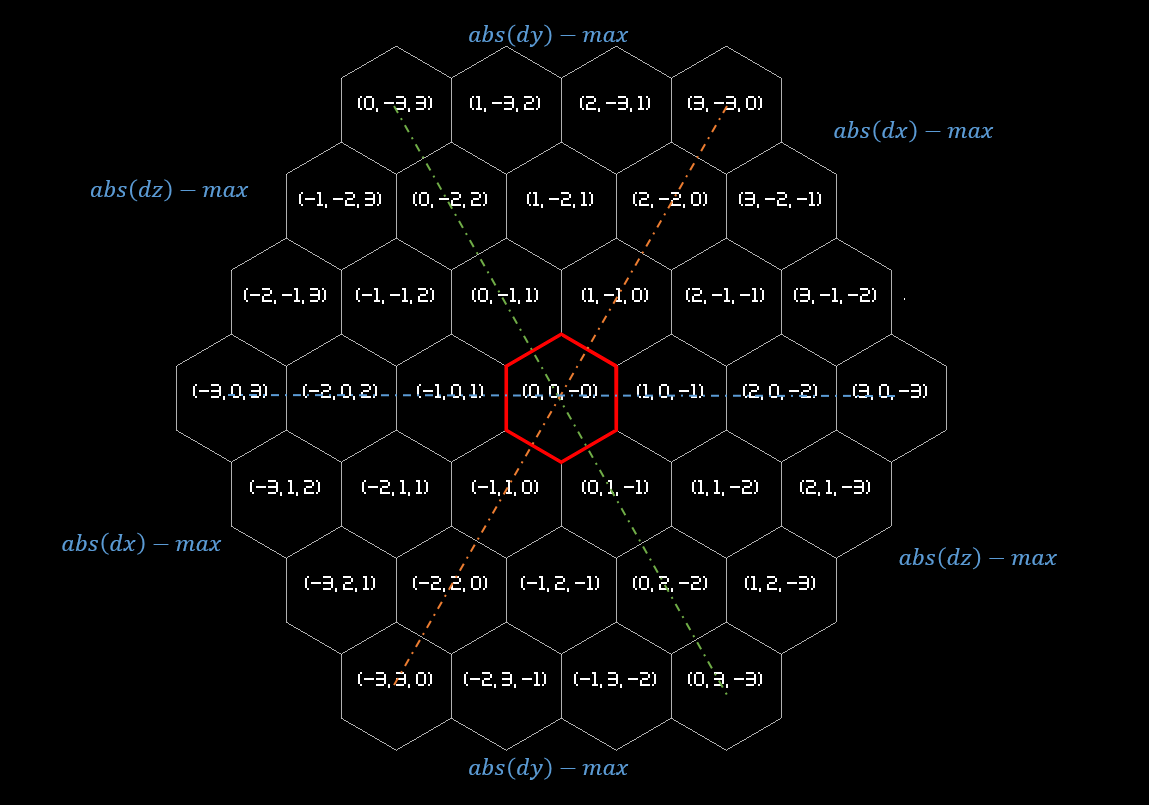
Теперь все, что нам нужно, это выбрать нужную часть и, сравнив модули не наибольших координат, выдать одно из осевых направлений, представленное в виде направляющей ячейки. Прямо на осях одна из координат всегда равна нулю, поэтому просто перехватим их как особые случаи. Для указания вдоль оси будем использовать знак разности конечного и начального шестиугольников. Также заметим, что на диагональных ячейках модули не наибольших координат равны, поэтому мы можем смещаться в любую из двух осей. Я выбрал смещение в сторону оси по часовой стрелке, в коде это выражается строгостью знаком сравнения. Для смещения против часовой стоит допустить равентсво. Так выглядит этот алгоритм в коде:
func direct_hex(hex1:Vector2, hex2:Vector2):var dx = hex2.x - hex1.xvar dy = hex2.y - hex1.yvar dz = -hex2.x-hex2.y + hex1.x+hex1.yif dx == 0: # Ось yreturn Vector2(0, sign(dy)) # Возвращаем ось yelif dy == 0: # Ось xreturn Vector2(sign(dx), 0) # Возвращаем ось xelif dz == 0: # Ось zreturn Vector2(sign(dx), sign(dy)) # Возвращаем ось zelse:if abs(dz) > abs(dx) and abs(dz) > abs(dy): # модуль разности по z оказался наибольшимif abs(dx) > abs(dy): # т.к. разность по x больше, значит мы отошли по x дальше, чем по y, значит выдаем ось xreturn Vector2(sign(dx), 0) # возвращаем ось xelse: # т.к. разность по y больше, значит мы отошли по y дальше, чем по x, значит выдаем ось yreturn Vector2(0, sign(dy)) # возвращаем ось y elif abs(dy) > abs(dx): # модуль разности по y оказался наибольшимif abs(dz) > abs(dx): # по аналогииreturn Vector2(0, sign(dy)) # возвращаем y. Это связанно с представлением z-координаты через две другиеelse: # по аналогииreturn Vector2(sign(dx), sign(dy)) # возвращаем z else: # модуль разности по x оказался наибольшимif abs(dy) > abs(dz): # по аналогииreturn Vector2(sign(dx), sign(dy)) # возвращаем zelse: # по аналогииreturn Vector2(sign(dx), 0) # возвращаем x
Опять же, тому кто читал мою статью про прямоугольные сетки, понять все это будет проще, ведь в ней я разбирал подобный алгоритм подробнее, однако, я надеюсь, что по комментариям принцип работы алгоритма понятен. Как мы видим, все рабоатет:
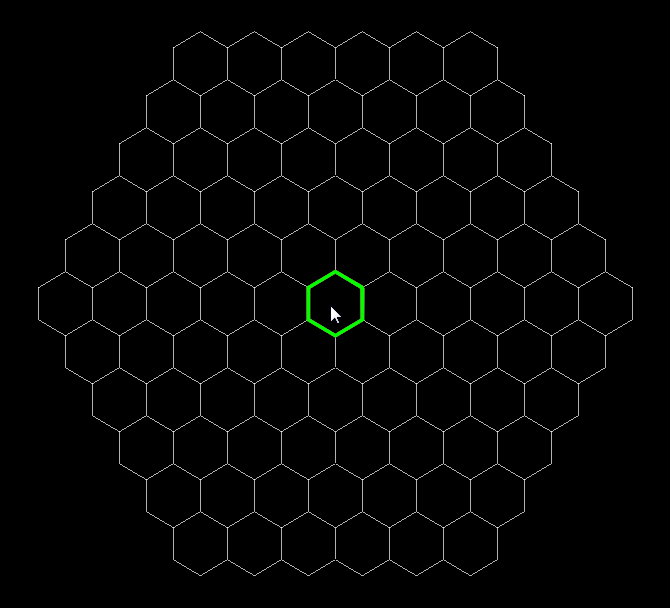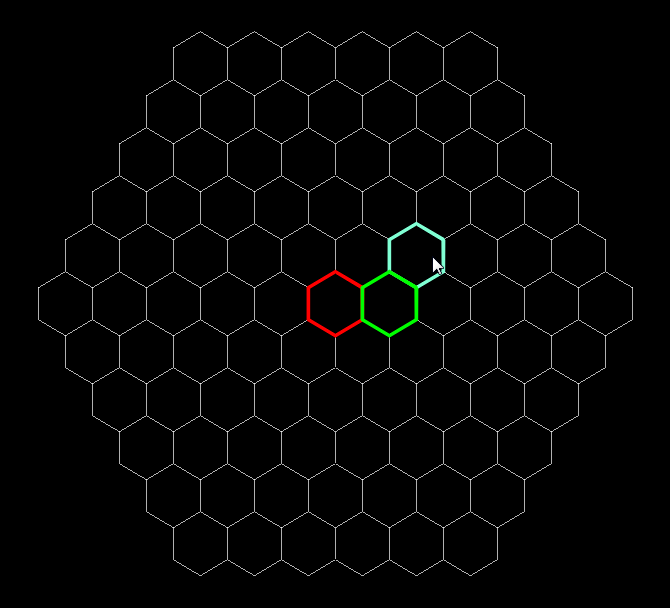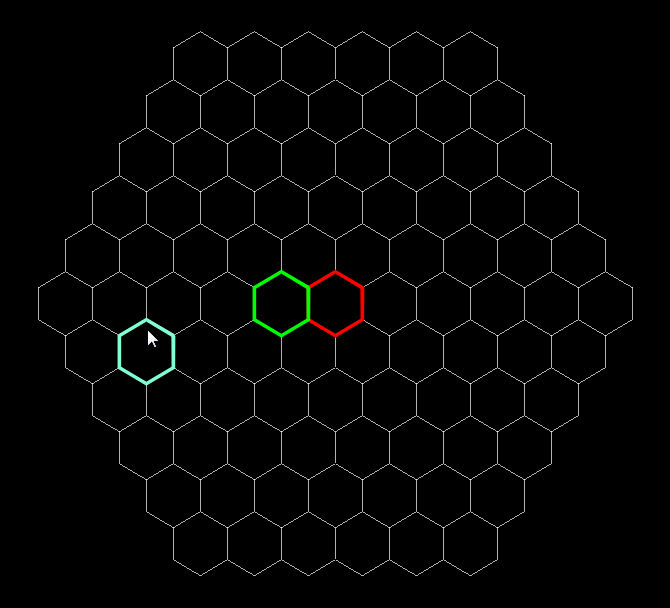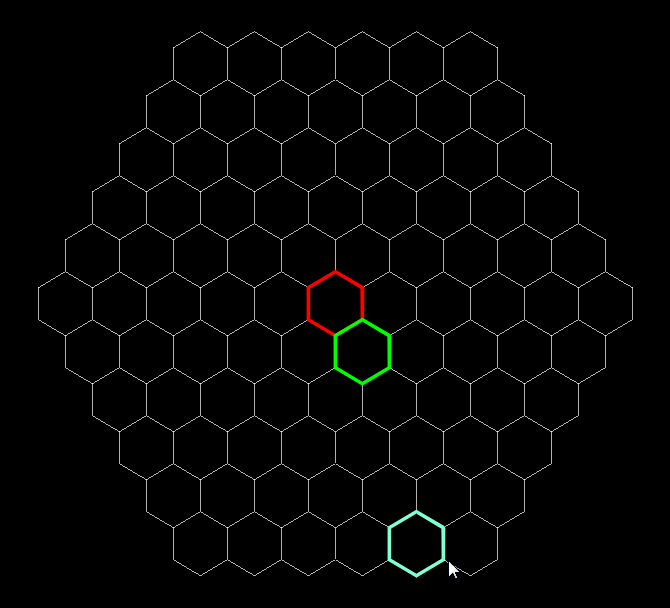
На всякий случай скажу, что этот алгоритм не зависит от ориентации шестиугольников, ведь работа идет с их координатами, а координатм внутри сетки вообще плевать на положение шестиугольников в пространстве.
Поиск пути
Основной алгоритм поиска пути тот же, что и у обычной прямоугольной сетки, отличаются только соседи и проверки на нахождение точки внутри карты. Главный алгоритм - A*, его не трогаем совсем.
Соседи у шестиугольника выглядят как то так:

Можно заметить, что они также не зависят от ориентации шестиугольников, поэтому в будущем будем пользоваться одной функцией для обоих случаев.
Также у разных видов карты отличаются проверки на принадлежность шестиугольниа им. Алгоритмы для разных ориентаций шестиугольников немного отличаеются, но в целом они похожи, поэтому пояснять я буду только на примере горизонтальных, а для вертикальных оставлю уже готовые функции.
Начнем с прямоугольной карты. Для наглядности напомню как она выглядит:
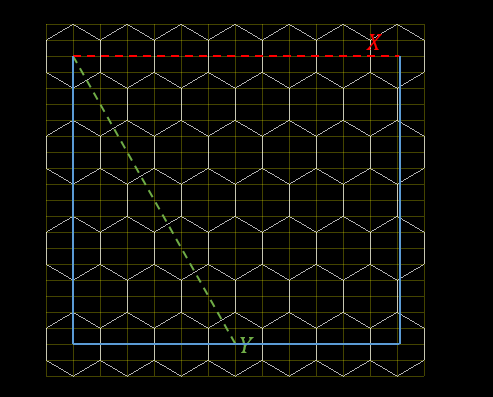
Синим обозначены границы карты. Оси в такой сетке идут не
параллельно сторонам прямоугольника, поэтому просто ограничить их
нулем и границей карты не выйдет. Так сработает только для
Y оси сетки, а горизонтальные границы зависят от
смещения по Y. Перемещаясь вдоль оси Y,
расстояние до левой границы в ячейках вспомогательной сетки
увеличивается на единицу, значит на половину шестиугольника.
Аналогично с правой границей, тоолько до нее расттояние
уменьшается. При округлении левой границы используем
floor, т.к. когда граница проходит ровно между
шестиугольниками, мы вмыбираем тот, что внутри. По аналогии
используем ceil для правой границы:
func _in_rect_grid_hor(hex):return hex.x >= -floor(hex.y/2) and hex.x < hex_map_size.x-ceil(hex.y/2) and hex.y < hex_map_size.y and hex.y >= 0
Для вертикальной ориентации логика точно такая же. Вот функция для нее:
func _in_rect_grid_vert(hex):return hex.x >= 0 and hex.x < hex_map_size.x and hex.y >= -floor(hex.x/2) and hex.y < hex_map_size.y-ceil(hex.x/2)
Теперь про шестиугольную карту. Ее вид:

Для простоты вычислений будем считать границы от центра карты. Просто потыкав и посмотрев на координаты я пришел к следующим формулам центров:
# для горизонтальныхfunc _get_hor_hex_map_center():return Vector2(int((hex_map_size.x-1)/2), hex_map_size.x-1)# для вертикальныхfunc _get_vert_hex_map_center():return Vector2(hex_map_size.x-1, int((hex_map_size.x-1)/2))
Каждому смещению по Y соответствует уменьшение
длины ряда на единицу, так и будем задавать границы по x. В
качестве размеров, ограничивающих карту, возьмем диагональ. Как ее
вычислять я рассказывал ранее. Тогда по Y границами
будут просто половины этих диагоналей, а по X одна из
граней всегда параллельна оси Y, поэтому уменьшаться
будет либо правая либо левая граница. Какая именно можно понять по
вертикальной половине шестиугольника. Если мы находимся в верхней,
то уменьшается левая граница (т.к. правая параллельна оси
Y), если в нижней то уменьшается правая граница (т.к.
левая паралельна оси Y). А если мы находимся прямо на
горизонтальной диагонали то нам плевать, ведь на ней смещение по
Y равно нулю.
Вот функции, реализующие данную логику для обеих ориентаций:
# для горизонтальныхfunc _in_hex_grid_hor(hex): var center = _get_hor_hex_map_center() var diag = int(hex_map_size.x*2 - 1) hex -= center # Vector2 passed by value; getting hex regarding map center if hex.y < 0: return hex.x >= -diag/2+abs(hex.y) and hex.x <= diag/2 and hex.y >= -diag/2 and hex.y <= diag/2 else: return hex.x >= -diag/2 and hex.x <= diag/2-abs(hex.y) and hex.y >= -diag/2 and hex.y <= diag/2# для вертикальныхfunc _in_hex_grid_vert(hex): var center = _get_vert_hex_map_center() var diag = int(hex_map_size.x*2 - 1) hex -= center # Vector2 passed by value; getting hex regarding map center if hex.x < 0: return hex.y >= -diag/2+abs(hex.x) and hex.y <= diag/2 and hex.x >= -diag/2 and hex.x <= diag/2 else: return hex.y >= -diag/2 and hex.y <= diag/2-abs(hex.x) and hex.x >= -diag/2 and hex.x <= diag/2
Для проверки поставим условие, что для рисования шестиугольника под курсором он должен быть внутри сетки:

Отлично, теперь можно спокойно реализовывать алгоритм поиска пути:
Ищем путь истинный
class PriorityStack:var items:Arrayfunc _init():items = Array()func empty() -> bool:return items.size() == 0func put(item, priority:int) -> void:if empty():items.append([item, priority])elif priority <= items[0][1]:items.insert(0, [item, priority])elif priority > items[-1][1]:items.append([item, priority])else:for i in range(len(items)):if priority <= items[i][1]:items.insert(i, [item, priority])breakfunc take():return items.pop_front()[0]func in_map(hex):match grid_type:GridTypes.hex:if hex_type == HexTypes.hor:return _in_hex_grid_hor(hex)else: # Verticalreturn _in_hex_grid_vert(hex)GridTypes.rect:if hex_type == HexTypes.vert:return _in_rect_grid_vert(hex)else: # Hor orientationreturn _in_rect_grid_hor(hex)func can_stand(hex:Vector2, obsts:PoolVector2Array):return in_map(hex) and not (hex in obsts)func neighbors(hex_pos:Vector2, obsts:PoolVector2Array):var res:PoolVector2Array = []var _neighbors = PoolVector2Array([Vector2(-1, 0), Vector2(1, -1), Vector2(0, -1), Vector2(1, 0), Vector2(0, 1), Vector2(-1, 1)])for i in _neighbors:if can_stand(i+hex_pos, obsts):res.append(i+hex_pos)return resfunc find_path(start:Vector2, goal:Vector2, obsts:PoolVector2Array):var frontier = PriorityStack.new()frontier.put(start, 0)var came_from = {}var cost_so_far = {}came_from[start] = startcost_so_far[start] = 0var current:Vector2var new_cost:intif not can_stand(goal, obsts):return PoolVector2Array()while not frontier.empty():current = frontier.take()if current == goal:breakfor next in neighbors(current, obsts):new_cost = cost_so_far[current] + 1if not (next in cost_so_far) or new_cost < cost_so_far[next]:cost_so_far[next] = new_costfrontier.put(next, new_cost+hex_distance(goal, next))came_from[next] = currentif frontier.empty() and current != goal:return PoolVector2Array()current = goalvar path = PoolVector2Array([current])while current != start:current = came_from[current]path.append(current)path.invert()path.remove(0) # removes first positionreturn pathfunc hex_distance(hex1:Vector2, hex2:Vector2):var dif = (hex2-hex1)return (abs(dif.x) + abs(dif.y) + abs(-dif.x-dif.y))/2
Данный код я взял напрямую из своей реализации, так что некоторые моменты не освещены, за ненадобностью. Поглазеть на полный код сможете кликнув по ссылке в конце статьи. Так это выглядит:

Растеризация отрезка
Вот с растеризацией у шестиугольной сетки большие проблемы. Можно, конечно, придумать что нибудь с алгоритмом брезенхема для растеризации отрезков, однако я не думаю что вам нужно растеризовывать по 1000 отрезков за кадр, поэтому на оптимизацию позволим себе немного подзабить и воспользуемся линейной интерполяцией, которую, кстати, и предлагает автор популярной англоязычной статьи. Думаю почти все знают что такое линейная интерполяция, поэтому просто оставлю тут рализацию алгоритма:
Растеризуем нерастеризуемое
func rast_line(hex1, hex2):var N = hex_distance(hex1, hex2)if N == 0: return PoolVector2Array([hex1])var res = PoolVector2Array()for i in range(N+1):res.append(round_hex(lerp(hex1, hex2, i/N)))return res
Вот так это выглядит:
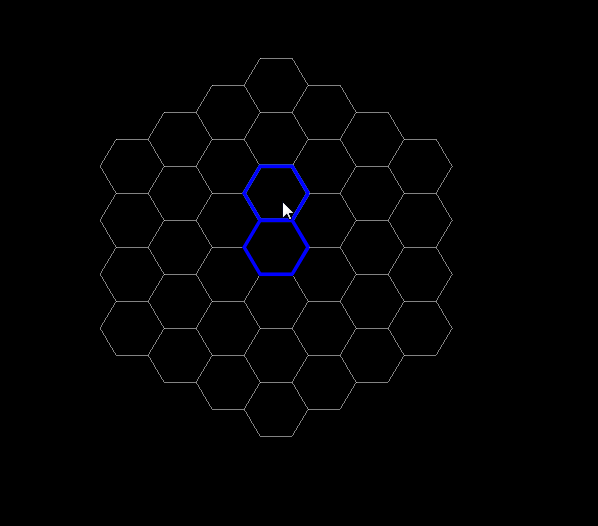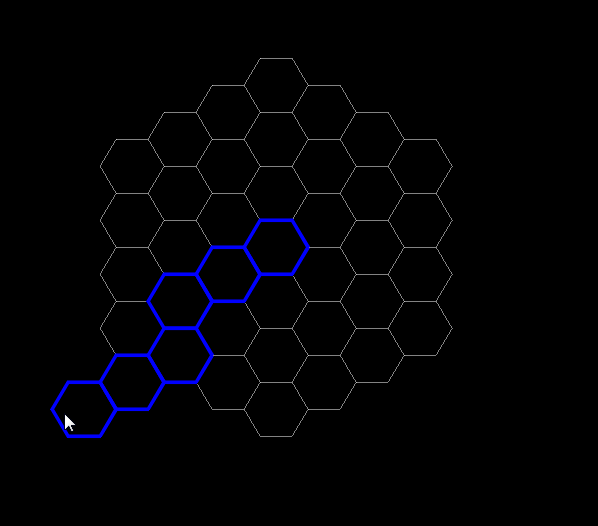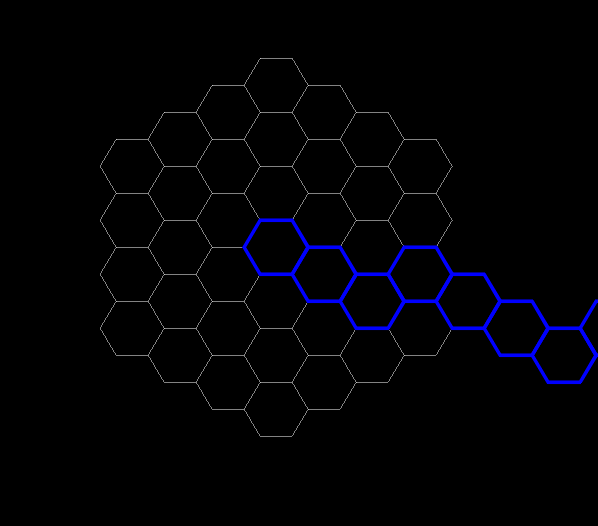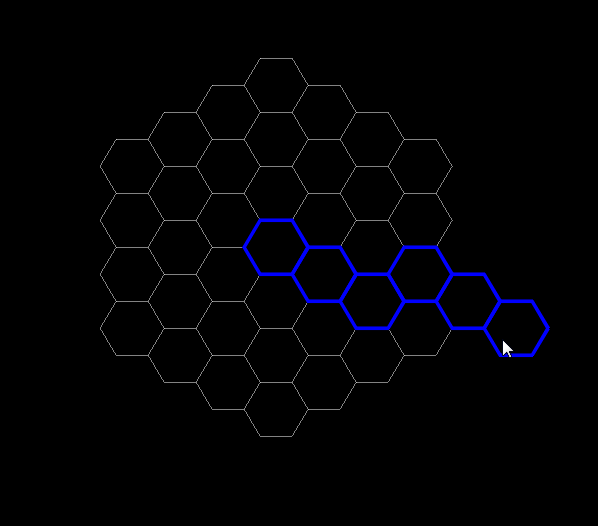
Пару слов в завершение
Вот и подошел столь запутанный рассказ к концу. Я постарался объяснить все максимально подробно и вставлял как можно больше картинок, надеюсь не зря. Никакую маленькую игру я делать не стал, ибо тут и так хаватаеn над чем подумать, поэтому просто оставлю код получившегося класса на почти 500 строк. Я подразумеваю его использование через автозагрузку, как собственно я и делал во время работы над ним.
Если я забыл про что рассказать или упустил какие то важные моменты, или же просто ошибаюсь, напишете об этом в комментарии.
Я надеюсь эта статья позволит вам полностью реализовать давние мечты по созданию "убийы героев" или что она позволила просто интересно провести вечер. До скорого!