Причины катастрофы были тщательно исследованы и сейчас у нас есть достаточно хорошее понимание того, что тогда случилось. Возможно, самый важный урок, который человечество вынесло из Чернобыльской катастрофы, заключается в том, что её причиной нельзя назвать недочёты конкретного реактора, или неправильные действия персонала в зале управления АЭС, или особенности отдельно взятого тоталитарного режима. Причиной происшествия такого масштаба стала целая цепь событий.

В пользу этой идеи говорит тот факт, что оставшиеся реакторы серии РБМК, включая три установки на Чернобыльской АЭС, функционировали без заметных проблем с 1986 года, а девять из них работают до сих пор. В ходе международного расследования причин возникновения Чернобыльской катастрофы в соответствующих отчётах МКГЯБ постоянно говорится о недостаточном уровне культуры безопасности.
Анализ обстоятельств, которые привели к созданию четвёртого энергоблока Чернобыльской АЭС и к последующему его использованию, потенциально опасному, может дать человечеству множество знаний о предотвращении катастроф. Это история о том, какую важную роль культура безопасности играет в отраслях промышленности, где цена аварий измеряется человеческими жизнями.
Анатомия катастрофы
За два года до аварии на Чернобыльской АЭС, в ночь на 3 декабря 1984 года, в индийском городе Бхопал погибло более двух тысяч человек. Тогда на близлежащем химическом заводе компании Union Carbide India Ltd случился выброс смертельно опасного вещества метилизоцианата. В последующие годы умерло ещё более тысячи человек, а общее число пострадавших составило около полумиллиона.

Заражённые почва и грунтовые воды вокруг завода, теперь заброшенного, до сих пор представляют опасность, но люди продолжают жить в тех местах.
К катастрофе в Бхопале привели низкий уровень технического обслуживания оборудования, неисправные средства защиты, а так же отсутствие культуры безопасности. Всё это вместе позволило воде проникнуть через неисправные вентили в резервуар с метилизоцианатом, что привело, в результате экзотермической реакции, к образованию смертоносного газа. Американская компания-владелец завода (теперь она называется The Dow Chemical Company) не очистила место аварии после закрытия завода в 1986 году. Теперь эта задача возложена на местные власти.
Катастрофа 1986 года в Чернобыле во многом похожа на аварию в Бхопале. В частности недостаточным уровнем культуры безопасности. Всё началось ещё на этапе проектирования реактора РБМК (реактор большой мощности канального типа), когда, ради экономии, было решено использовать природный уран, а не обогащённый уран-235. Это означало увеличение размеров реактора, что привело к принятию решения о том, что в конструкции реактора не нужен корпус, который имеется у реакторов других типов (например у корпусных водо-водяных энергетических реакторов, ВВЭР). Корпус РБМК оказался бы слишком большим и слишком дорогим.
В РБМК имеется множество систем обеспечения безопасности, включая применение независимых петель контура охлаждения реактора, использования системы аварийного охлаждения реактора (САОР) и системы аварийного отключения реактора (SCRAM). Но там не было чего-то такого, что не дало бы операторам реактора по собственному усмотрению отключить все эти системы безопасности. В результате то, что должно было стать простым испытанием турбогенератора в режиме выбега (что предусматривало использование кинетической энергии, запасённой во вращающемся роторе турбогенератора, для выработки электроэнергии, необходимой для питания циркуляционных насосов в аварийной ситуации), превратилось в катастрофу.
Игры с реактивностью реактора
У каждого легководного реактора, где для охлаждения ядра реактора используется обычная вода, есть два основных параметра, которые позволяют узнать о том, в каком режиме работает реактор в номинальном, или нет, отклоняясь от него в большую или меньшую сторону. Они имеют отношение к реактивности реактора к количеству нейтронов с определённой скоростью (температурой нейтронов), присутствующих в некий момент времени в нейтронном эффективном сечении используемого в реакторе топлива.
В случае с ураном-235 необходимы так называемые тепловые нейтроны, но в ходе цепной ядерной реакции производится множество более быстрых нейтронов (их называют быстрыми нейтронами). Быстрые нейтроны могут быть замедлены до состояния тепловых нейтронов с использованием замедлителей нейтронов. Это повышает реактивность реактора. Для снижения реактивности реактора используются поглотители нейтронов, которые могут быть представлены водой и управляющими стержнями, которые часто делают из карбида бора.
В большинстве легководных реакторов обычная вода используется и для замедления нейтронов, и для поглощения нейтронов. А это значит, что если реактивность реактора возрастает, повышается скорость закипания воды, что увеличивает количество пара. Появление пара означает ухудшение возможностей замедления нейтронов, а это, в свою очередь, приводит к уменьшению количества имеющихся тепловых нейтронов, что создаёт цикл отрицательной обратной связи. Это то, что называется отрицательным паровым коэффициентом реактивности.

У интересующего нас реактора РБМК второго поколения много общего с прототипом ядерного реактора первого поколения, в котором используется графитовый замедлитель. Собственно говоря, в РБМК графит тоже использовался в роли замедлителя нейтронов. Хотя это позволяло применять природный уран, это ещё и означало то, что РБМК работал с положительным паровым коэффициентом реактивности. Когда вода в контуре охлаждения реактора закипала и в ней возникали пузырьки, её возможности по поглощению нейтронов ухудшались, а эффект замедления нейтронов не менялся, что создавало возможность возникновения бесконтрольной ядерной реакции.
Эта неоднозначная особенность была признана приемлемой, так как она позволяла реакторам РБМК выдавать тепловую мощность, значительно превышающую ту, которую обеспечивали западные реакторы того времени. Предполагалось, что у хорошо обученного персонала не будет проблем с управлением реактором РБМК.
Как уже было бесчисленное количество раз доказано, например, когда затонул Титаник, менеджеры и маркетологи регулярно берут верх над инженерами. Любая катастрофа, которой можно было бы избежать за счёт правильного обслуживания техники и тщательного обучения персонала, становится неизбежной в условиях отсутствия культуры безопасности.
Закон Мёрфи в действии
Когда было запланировано отключение четвёртого энергоблока Чернобыльской АЭС для обслуживания, было решено провести на нём эксперимент с турбогенератором, для чего была отключена САОР. Но, прямо перед тем, как было запланировано начать эксперимент, решено было оставить реактор в работающем состоянии ещё на 11 часов, так как энергосеть нуждалась в энергии, вырабатываемой энергоблоком. Эта задержка привела к тому, что персонал дневной смены, который и должен был проводить эксперимент, сменился сотрудниками вечерней смены. Им, как результат, из-за отключённой САОР, пришлось вручную регулировать вентили гидравлической системы реактора.
Когда на службу пришли работники ночной смены, ожидающие, что им придётся иметь дело с остановленным и остывающим реактором, им сообщили о том, что эксперимент должны проводить они. Это означало, что мощность реактора нужно было снизить, перейти с полной мощности к 700 1000 МВт (тепловых), а потом прекратить подачу пара на турбину.

У реактора РБМК есть одна особенность, которая выражается в том, что он крайне нестабилен и сложен в управлении на низких уровнях мощности. Учитывая положительный паровой коэффициент реактивности, несовершенство конструкции управляющих стержней и образование, в качестве побочного продукта работы реактора, ксенона-135, поглощающего много нейтронов, мощность реактора упала менее чем до 100 МВт. Это привело к тому, что операторы начали убирать всё больше и больше управляющих стержней (включая стержни, имеющие отношение к автоматической системе управления) в попытке увеличить реактивность реактора. Это позволило реактивности медленно вырасти и дойти до уровней, близких к тем, которые требовались для проведения эксперимента.
Поток охлаждающей жидкости в ядре реактора был усилен для получения большего количества пара, но это понизило реактивность, поэтому два насоса были остановлены для того чтобы снова повысить реактивность реактора. В этой ситуации, когда практически все управляющие стержни были вынуты из реактора, и когда были отключены все системы безопасности, эксперимент свернули, несмотря на то что падение мощности, выдаваемой замедляемым генератором, привело к понижению давления воды, охлаждающей реактор. И, наконец, было принято решение воспользоваться системой аварийного отключения реактора, что привело бы к сравнительно быстрому вводу управляющих стержней в реактор для его остановки.
Стержни вытесняли воду из каналов, создавая пустоты, а графит на концах стержней способствовал повышению реактивности реактора. В результате роста реактивности в нижней части реактора теплоотдача реактора подскочила примерно до 30000 МВт (при номинальной теплоотдаче в 3000 МВт). Вода, охлаждающая реактор, немедленно закипела, циркониевая оболочка топливных стержней расплавилась, она прореагировала с паром, а в результате этой реакции выделился водород.
Первым взрывом (возможно, его причиной стал перегретый пар) сбросило крышку реактора и повредило крышу здания. Второй взрыв, который произошёл через несколько секунд (это, вероятно, взорвалась смесь водорода с кислородом), разрушил ядро реактора и прекратил цепную ядерную реакцию. Всё, что осталось от реактора 4, представляло собой разбросанные повсюду радиоактивные фрагменты ядра реактора и раскалённый кориум лаваподобная масса, состоящая из компонентов расплавленной активной зоны ядерного реактора, которая затекла в подвал здания реактора. Тем временем в ядре реактора загорелся графит, в воздух поднялся столб радиоактивного дыма, что и привело к тому, что в Швеции обнаружили следы радиационного заражения.
Конец эпохи РБМК
В наши дни всё ещё работают девять реакторов РБМК. Все они расположены в России. А три реактора, оставшиеся на Чернобыльской АЭС, были постепенно выведены из эксплуатации. Работающие реакторы РБМК усовершенствовали, учтя опыт катастрофы. А именно, речь идёт о следующих улучшениях:
- Использование топлива с более высоким уровнем обогащения урана, что позволяет скомпенсировать наличие дополнительных управляющих стержней.
- Использование большего количества поглотителей нейтронов для стабилизации реактора на низких уровнях мощности.
- Ускорение работы системы аварийного отключения реактора (12 секунд вместо 18).
- Ограничение доступа к органам управления реактором, отключающим системы безопасности.
Вот главные следствия этих изменений: значительно уменьшился положительный паровой коэффициент реактивности, реактором стало намного легче управлять на низких уровнях мощности, у операторов стало гораздо меньше возможностей для импровизаций.
Учитывая то, что реакторы типа РБМК и подобные им в наши дни совершенно не пользуются поддержкой общественности, в России будущее атомной электроэнергетики строится на реакторах типа ВВЭР. В частности, речь идёт о реакторе ВВЭР-1200, относящемуся к поколению 3+. В таких реакторах обычная вода используется для замедления нейтронов, для охлаждения реактора, а так же для поглощения нейтронов. Такие реакторы, при создании которых соблюдаются международные стандарты безопасности, заменят в будущие годы оставшиеся на российских атомных электростанциях реакторы РБМК.
Всё дело в культуре безопасности
Интересным противопоставлением идее о том, что реактор РБМК так опасен из-за положительного парового коэффициента реактивности, являются принципы, по которым построены реакторы CANDU (Canada Deuterium Uranium тяжеловодные водо-водяные ядерные реакторы производства Канады). Эти реакторы привлекают к себе так мало внимания, что обычные люди, не являющиеся гражданами Канады, обычно не знают о том, что в Канаде есть атомная промышленность, и о том, что Канада экспортирует эти реакторы во многие страны.
При этом в реакторах CANDU изначально использовался природный уран и они отличаются положительным паровым коэффициентом реактивности. Но, несмотря на это, активные и пассивные системы защиты таких реакторов способны предотвратить нечто вроде тех ошибок персонала, которые были совершены в Чернобыле, или что-то вроде частичного расплавления активной зоны реактора (при отрицательном паровом коэффициенте реактивности) при аварии на АЭС Три-Майл-Айленд. В последнем случае оператор взял на себя управление системой безопасности, в результате события развивались по сценарию, напоминающему неудачный эксперимент в Чернобыле.
Похожие причины лежат в основе аварии на АЭС Фукусима-1, которая произошла в 2011 году в Японии. Об этом говорится в отчёте Национального парламента Японии. Низкий уровень культуры безопасности и широкое распространение коррупции, доходящей до высших правительственных кругов, привело к тому, что системы безопасности электростанции не поддерживались в актуальном состоянии. АЭС не вполне соответствовала стандартам устойчивости к землетрясениям. Она не была модернизирована в соответствии с рекомендациями американской регулирующей организации.

Но, даже учитывая вышесказанное, происшествия на атомных электростанциях чрезвычайно редки, благодаря чему атомная энергетика входит в число самых безопасных форм генерирования электроэнергии (с учётом количества выработанной энергии). Пожалуй, даже большее беспокойство, чем отдельные инциденты, вызывает то, что низкая культура безопасности характерна не только для атомной промышленности. Похожая ситуация наблюдается и во многих других сферах, о чём красноречиво говорят авария в Бхопале и другие крупные техногенные катастрофы. В США за расследование происшествий в сфере химической промышленности отвечает Совет по химической безопасности и расследованию угроз (Chemical Safety and Hazard Investigation Board, CSB).
CSB занимается, помимо подготовки официальных отчётов, съёмкой документальных фильмов, которые можно найти на его YouTube-канале. Авторы этих материалов стремятся донести до сознания читателей и зрителей тот факт, что культура безопасности это не что-то такое, что можно принимать как данность, или что-то такое, на что можно вообще не обращать внимания, не опасаясь каких-либо проблем. В США, несмотря на то, что режим там вовсе не тоталитарный, почему-то регулярно происходят промышленные катастрофы, которые убивают и калечат сотни человек.
Из отчётов CSB можно сделать вывод о том, что, хотя радиоактивные материалы и могут выглядеть довольно-таки страшными, не стоит недооценивать опасность чего-то, на первый взгляд, совершенно невинного, вроде древесных опилок или муки. И если хотя бы допускать существование опасных ситуаций это уже будет первым шагом к тому, что кто-то сможет назвать худшим рабочим днём в своей жизни. У этого правила нет исключений.
В безопасности нет такого понятия, как Я
Никому не хотелось бы быть тем самым членом команды, которому приходится указывать другим на очевидные огрехи в безопасности, связанные с конструкцией каких-то устройств или с выполнением каких-то процедур. И, точно так же, никого не прельстит перспектива быть стукачом, который закладывает своих коллег, нарушающих правила техники безопасности. Но, в то же время, один человек не в состоянии склонить целую компанию или страну к совершенствованию процедур обеспечения безопасности.
Для того чтобы создавать и внедрять правила безопасности, для того, чтобы им следовать, не нужно прилагать непомерных усилий. Но, если безопасности уделяется мало внимания, значит возникновение очередной катастрофы, которую легко можно было бы предотвратить, это лишь вопрос времени, в чём бы такая катастрофа ни выражалась. Правила безопасности нельзя назвать чем-то невероятно привлекательным или вызывающим всеобщее восхищение. Но часто они представляют собой именно ту границу, которая отделяет скучный рабочий день от дня, в который завод сравняло с землёй взрывом, унёсшим множество жизней, или от дня аварии, в результате которой смесь угольной золы с водой превратила всё вокруг в пустыню.
Мы должны помнить не только о Чернобыле, но и о Бхопале, и о других подобных катастрофах, которые забрали уже очень много жизней и продолжат их забирать до тех пор, пока мы, как общество, не сделаем культуру безопасности частью повседневной жизни в каждом уголке Земли.
Как вы оцениваете уровень культуры безопасности, сложившийся в той сфере, в которой вы работаете?



 Импульсы от америция с детектора,
сделанного абы как (слева) и после доработки (справа)
Импульсы от америция с детектора,
сделанного абы как (слева) и после доработки (справа)

 Скотт Филд (слева) и Гаурав Ханна не
ожидали, что их допущение будет работать для чёрных дыр с
сопоставимыми массами
Скотт Филд (слева) и Гаурав Ханна не
ожидали, что их допущение будет работать для чёрных дыр с
сопоставимыми массами
 Детектор LIGO в г. Хэнфорде, штат
Вашингтон, имеет две длинные стрелы, расположенные под прямым
углом. Лазеры внутри каждой стрелы измеряют относительную разницу
длин каждой из стрел при прохождении гравитационной волны
Детектор LIGO в г. Хэнфорде, штат
Вашингтон, имеет две длинные стрелы, расположенные под прямым
углом. Лазеры внутри каждой стрелы измеряют относительную разницу
длин каждой из стрел при прохождении гравитационной волны
 Гравитационные волны, возникающие
вследствие столкновения чёрных дыр, практически одновременно
поступают на детекторы LIGO в Вашингтоне (оранжевый) и Луизиане
(синий), а также на детектор Virgo в Италии
Гравитационные волны, возникающие
вследствие столкновения чёрных дыр, практически одновременно
поступают на детекторы LIGO в Вашингтоне (оранжевый) и Луизиане
(синий), а также на детектор Virgo в Италии
 Визуализация слияния чёрных дыр с
соотношением масс 9,2 к 1. Видео начинается примерно за 10 секунд
до столкновения. Слева показан полный спектр гравитационного
излучения, окрашенный в соответствии с уровнем сигнала: синий цвет
слабый сигнал, оранжевый сильный. Справа показаны различные
компоненты гравитационного сигнала
Визуализация слияния чёрных дыр с
соотношением масс 9,2 к 1. Видео начинается примерно за 10 секунд
до столкновения. Слева показан полный спектр гравитационного
излучения, окрашенный в соответствии с уровнем сигнала: синий цвет
слабый сигнал, оранжевый сильный. Справа показаны различные
компоненты гравитационного сигнала

 Две чёрные дыры, каждая с аккреционным
диском, изображаются незадолго до столкновения. С новым сообщением
GW190521 мы нашли самые тяжелые массивные чёрные дыры, когда-либо
обнаруженные в гравитационных волнах, их масса превышает 100
солнечных масс, они впервые раскрывают массу переходной чёрной дыры
Две чёрные дыры, каждая с аккреционным
диском, изображаются незадолго до столкновения. С новым сообщением
GW190521 мы нашли самые тяжелые массивные чёрные дыры, когда-либо
обнаруженные в гравитационных волнах, их масса превышает 100
солнечных масс, они впервые раскрывают массу переходной чёрной дыры
 Когда чёрная дыра и звезда-компаньон
вращаются друг вокруг друга, движение звезды со временем изменяется
из-за гравитационного влияния чёрной дыры, в это же время чёрная
дыра обрастает веществом звезды, порождая рентгеновское и
радиоизлучение. Если вместо звезды на орбите вращается другая
чёрная дыра, будет преобладать гравитационное излучение (ЦЗИНЧУАНЬ
ЮЙ/ПЕКИНСКИЙ ПЛАНЕТАРИЙ/2019год)
Когда чёрная дыра и звезда-компаньон
вращаются друг вокруг друга, движение звезды со временем изменяется
из-за гравитационного влияния чёрной дыры, в это же время чёрная
дыра обрастает веществом звезды, порождая рентгеновское и
радиоизлучение. Если вместо звезды на орбите вращается другая
чёрная дыра, будет преобладать гравитационное излучение (ЦЗИНЧУАНЬ
ЮЙ/ПЕКИНСКИЙ ПЛАНЕТАРИЙ/2019год)
 Из-за эффектов как высокой скорости
(специальная теория относительности), так и кривизны пространства
(общая теория относительности) звезда, проходящая рядом с чёрной
дырой, должна подвергнуться ряду важных воздействий, которые
приведут к физическим наблюдаемым явлениям, таким как красное
смещение её света и небольшое, но значительное изменение её
эллиптической орбиты. Сближение S02 в мае 2018 года было лучшим
шансом, предоставленным нам, чтобы исследовать эти релятивистские
эффекты и тщательно изучить предсказания Эйнштейна (ESO/M.
KORNMESSER)
Из-за эффектов как высокой скорости
(специальная теория относительности), так и кривизны пространства
(общая теория относительности) звезда, проходящая рядом с чёрной
дырой, должна подвергнуться ряду важных воздействий, которые
приведут к физическим наблюдаемым явлениям, таким как красное
смещение её света и небольшое, но значительное изменение её
эллиптической орбиты. Сближение S02 в мае 2018 года было лучшим
шансом, предоставленным нам, чтобы исследовать эти релятивистские
эффекты и тщательно изучить предсказания Эйнштейна (ESO/M.
KORNMESSER)
 При слиянии двух движущихся объектов
порождается огромное количество гравитационных волн. Простое
путешествие через искривлённое пространство отличный способ
заставить массивные частицы излучать гравитационные волны. В этом
заключается фундаментальная разница между гравитацией Эйнштейна и
гравитацией Ньютона
При слиянии двух движущихся объектов
порождается огромное количество гравитационных волн. Простое
путешествие через искривлённое пространство отличный способ
заставить массивные частицы излучать гравитационные волны. В этом
заключается фундаментальная разница между гравитацией Эйнштейна и
гравитацией Ньютона
 Гравитационное движение Земли вокруг
Солнца не связано с невидимым гравитационным притяжением, но лучше
описывается свободным падением Земли в искривлённом пространстве,
большая часть кривизны которого порождается Солнцем. Кратчайшее
расстояние между двумя точками не прямая линия, а геодезическая:
кривая линия, которая определяется гравитационной деформацией
пространства-времени. Проходя через такое искривлённое
пространство, Земля испускает гравитационные волны (LIGO/T. PYLE)
Гравитационное движение Земли вокруг
Солнца не связано с невидимым гравитационным притяжением, но лучше
описывается свободным падением Земли в искривлённом пространстве,
большая часть кривизны которого порождается Солнцем. Кратчайшее
расстояние между двумя точками не прямая линия, а геодезическая:
кривая линия, которая определяется гравитационной деформацией
пространства-времени. Проходя через такое искривлённое
пространство, Земля испускает гравитационные волны (LIGO/T. PYLE)
 Пульсар с массивным двойным компаньоном,
особенно компактным компаньоном, таким как белый карлик, другая
нейтронная звезда или чёрная дыра может испускать значительное
количество гравитационных волн. Такое излучение вызовет изменение
временных наблюдений пульсара, что позволит проверить теорию
относительности (ESO/L. CALADA)
Пульсар с массивным двойным компаньоном,
особенно компактным компаньоном, таким как белый карлик, другая
нейтронная звезда или чёрная дыра может испускать значительное
количество гравитационных волн. Такое излучение вызовет изменение
временных наблюдений пульсара, что позволит проверить теорию
относительности (ESO/L. CALADA)
 Релятивистский прогноз (красная линия) и
ньютоновский прогноз (зелёная линия) в сравнении с данными двойного
пульсара (чёрные точки). С самого первого открытия двойной
нейтронной звездной системы мы знали, что гравитационное излучение
уносит энергию. Поиск системы на завершающих стадиях движения по
спирали и слияния был только вопросом времени (НАСА (L),
РАДИОАСТРОНОМИЧЕСКИЙ ИНСТИТУТ МАКСА ПЛАНКА/МАЙКЛ КРАМЕР)
Релятивистский прогноз (красная линия) и
ньютоновский прогноз (зелёная линия) в сравнении с данными двойного
пульсара (чёрные точки). С самого первого открытия двойной
нейтронной звездной системы мы знали, что гравитационное излучение
уносит энергию. Поиск системы на завершающих стадиях движения по
спирали и слияния был только вопросом времени (НАСА (L),
РАДИОАСТРОНОМИЧЕСКИЙ ИНСТИТУТ МАКСА ПЛАНКА/МАЙКЛ КРАМЕР)
 Рябь пространства-времени, порождаемая
орбитальными массами, возникает независимо от конечного продукта
слияния. Однако большая часть высвобождаемой энергии исходит только
на нескольких последних орбитальных витках и во время фактического
слияния двух масс, которые проходят стадии вращения по спирали и
слияния (Р. ХАРТ CALTECH/JPL)
Рябь пространства-времени, порождаемая
орбитальными массами, возникает независимо от конечного продукта
слияния. Однако большая часть высвобождаемой энергии исходит только
на нескольких последних орбитальных витках и во время фактического
слияния двух масс, которые проходят стадии вращения по спирали и
слияния (Р. ХАРТ CALTECH/JPL)
 На этом графике показаны массы всех
компактных двойных звёзд, обнаруженных LIGO/Virgo: чёрные дыры,
отмеченные синим цветом, и нейтронные звёзды, отмеченные оранжевым
цветом. Также показаны чёрные дыры с массами звёзд (фиолетовые) и
нейтронные звёзды (жёлтые), обнаруженные с помощью наблюдений
электромагнитных волн. Всего у нас более 50 наблюдений событий
излучения гравитационных волн, соответствующих слиянию компактных
масс (LIGO/VIRGO/СЕВЕРО-ЗАПАДНЙ УНИВЕРСИТЕТ/ФРЭНК ЭЛАВСКИ)
На этом графике показаны массы всех
компактных двойных звёзд, обнаруженных LIGO/Virgo: чёрные дыры,
отмеченные синим цветом, и нейтронные звёзды, отмеченные оранжевым
цветом. Также показаны чёрные дыры с массами звёзд (фиолетовые) и
нейтронные звёзды (жёлтые), обнаруженные с помощью наблюдений
электромагнитных волн. Всего у нас более 50 наблюдений событий
излучения гравитационных волн, соответствующих слиянию компактных
масс (LIGO/VIRGO/СЕВЕРО-ЗАПАДНЙ УНИВЕРСИТЕТ/ФРЭНК ЭЛАВСКИ)
 Какая часть массы преобразуется в
гравитационные волны при слиянии двух чёрных дыр? Обратите
внимание, что, хотя график, очевидно, показывает большие вариации в
зависимости от соотношения масс, масштаб по оси y очень мал, и 10%
даёт хорошее приближение в широком диапазоне соотношений масс
(ВИДЖАЙ ВАРМА)
Какая часть массы преобразуется в
гравитационные волны при слиянии двух чёрных дыр? Обратите
внимание, что, хотя график, очевидно, показывает большие вариации в
зависимости от соотношения масс, масштаб по оси y очень мал, и 10%
даёт хорошее приближение в широком диапазоне соотношений масс
(ВИДЖАЙ ВАРМА)
 В нижней части анимации показан сигнал
гравитационных волн (по амплитуде и частоте), генерируемых двумя
чёрными дырами примерно одинаковой массы при прохождении стадий
вращения по спирали и слияния. Такой сигнал гравитационных волн
распространяется в трёхмерном пространстве со скоростью света. Его
можно обнаружить с расстояния в миллиарды световых лет достаточно
точным детектором гравитационных волн (Н. ФИШЕР, Х. ПФАЙФФЕР, А.
БУОНАННО (ИНСТИТУТ ГРАВИТАЦИОННОЙ ФИЗИКИ ИМ. МАКСА ПЛАНКА),
МОДЕЛИРОВАНИЕ ЭКСТРЕМАЛЬНОГО ПРОСТРАНСТВА-ВРЕМЕНИ (SXS))
В нижней части анимации показан сигнал
гравитационных волн (по амплитуде и частоте), генерируемых двумя
чёрными дырами примерно одинаковой массы при прохождении стадий
вращения по спирали и слияния. Такой сигнал гравитационных волн
распространяется в трёхмерном пространстве со скоростью света. Его
можно обнаружить с расстояния в миллиарды световых лет достаточно
точным детектором гравитационных волн (Н. ФИШЕР, Х. ПФАЙФФЕР, А.
БУОНАННО (ИНСТИТУТ ГРАВИТАЦИОННОЙ ФИЗИКИ ИМ. МАКСА ПЛАНКА),
МОДЕЛИРОВАНИЕ ЭКСТРЕМАЛЬНОГО ПРОСТРАНСТВА-ВРЕМЕНИ (SXS))






 Вот как выглядит Солнце через сварочную
маску за 150 рублей
Вот как выглядит Солнце через сварочную
маску за 150 рублей
 Credit: timeanddate.com
Credit: timeanddate.com
 Степень понижения яркости изображения в
зависимости от предустановленного ND-фильтра
Степень понижения яркости изображения в
зависимости от предустановленного ND-фильтра
 300mm, f/45, 1/4000 sec, Солнце в 9:25
утра без сварочного стекла
300mm, f/45, 1/4000 sec, Солнце в 9:25
утра без сварочного стекла

 Те же настройки, но через сварочное
стекло. На экране частичное солнечное затмение от 21 июня 2020 года
Те же настройки, но через сварочное
стекло. На экране частичное солнечное затмение от 21 июня 2020 года
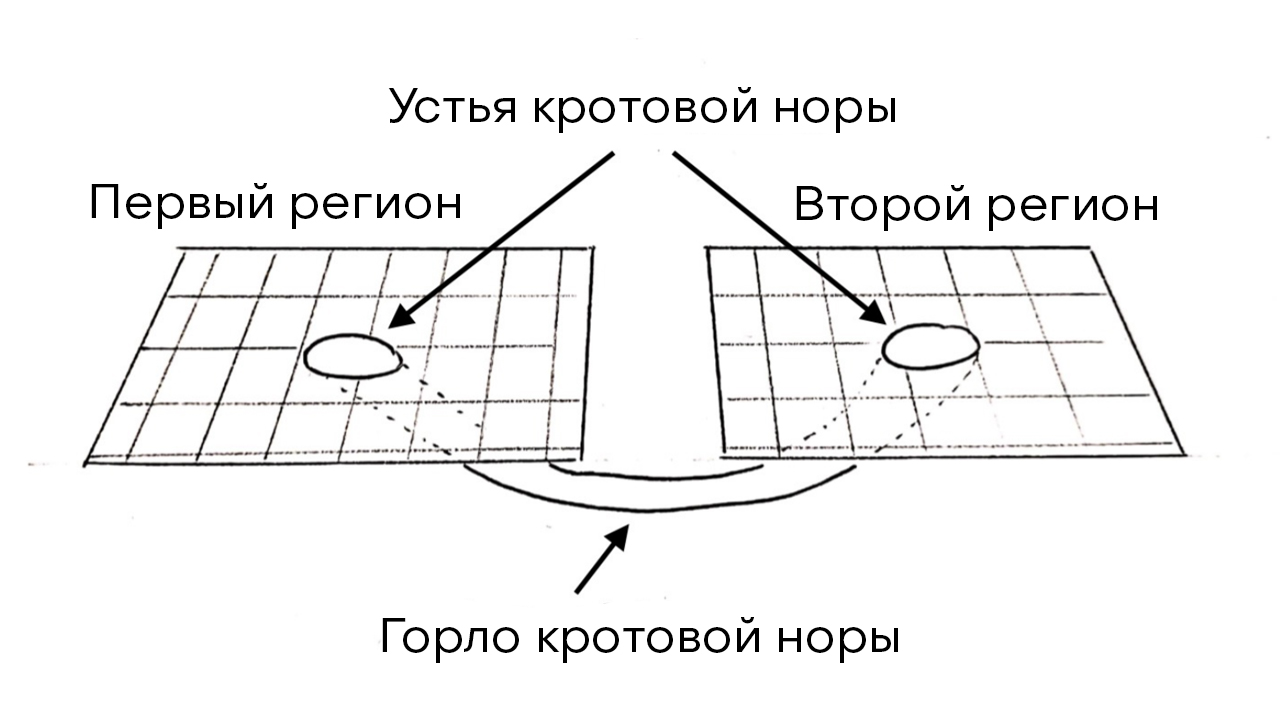 Рис.1: Если представить наше трехмерное
пространство в виде двухмерной поверхности, то червоточина может
быть представлена в виде цилиндрической поверхности, соединяющей
две области в одной вселенной или двух разных вселенных. Входы в
червоточину называются ее устьями, они соединяются горлом.
Рис.1: Если представить наше трехмерное
пространство в виде двухмерной поверхности, то червоточина может
быть представлена в виде цилиндрической поверхности, соединяющей
две области в одной вселенной или двух разных вселенных. Входы в
червоточину называются ее устьями, они соединяются горлом.
 Рис.2: Диаграмма Пенроуза для червоточины
Эйнштейна-Розена. Горло червоточины (горизонт), представлено двумя
пунктирными линиями (см. приложение 3). Примечание: уместно
заменить термин нулевой бесконечности на термин изотропной
бесконечности или светоподобной бесконечности (от англ.: null
infinity).
Рис.2: Диаграмма Пенроуза для червоточины
Эйнштейна-Розена. Горло червоточины (горизонт), представлено двумя
пунктирными линиями (см. приложение 3). Примечание: уместно
заменить термин нулевой бесконечности на термин изотропной
бесконечности или светоподобной бесконечности (от англ.: null
infinity).
![Рис.3: Эволюция интенсивности фонового источника при прохождении червоточины с эффективной отрицательной массой (слева) и нормального компактного объекта (справа). Кривые соответствуют значениям параметров воздействия; наименьший параметр воздействия характеризуется более выраженной модуляцией интенсивности источника и наоборот: от зеленого до красного. Иллюстрация взята из [34]. Рис.3: Эволюция интенсивности фонового источника при прохождении червоточины с эффективной отрицательной массой (слева) и нормального компактного объекта (справа). Кривые соответствуют значениям параметров воздействия; наименьший параметр воздействия характеризуется более выраженной модуляцией интенсивности источника и наоборот: от зеленого до красного. Иллюстрация взята из [34].](http://personeltest.ru/aways/habrastorage.org/getpro/habr/upload_files/06a/874/ef0/06a874ef04934b0867671f0573562794.jpg) Рис.3: Эволюция интенсивности фонового
источника при прохождении червоточины с эффективной отрицательной
массой (слева) и нормального компактного объекта (справа). Кривые
соответствуют значениям параметров воздействия; наименьший параметр
воздействия характеризуется более выраженной модуляцией
интенсивности источника и наоборот: от зеленого до красного.
Иллюстрация взята из [34].
Рис.3: Эволюция интенсивности фонового
источника при прохождении червоточины с эффективной отрицательной
массой (слева) и нормального компактного объекта (справа). Кривые
соответствуют значениям параметров воздействия; наименьший параметр
воздействия характеризуется более выраженной модуляцией
интенсивности источника и наоборот: от зеленого до красного.
Иллюстрация взята из [34].![Рис.4: Верхние границы доверительных вероятностей для плотности числа червоточин Эллиса во Вселенной (68% и 95%). Данные поиска квазаров Слоановского цифрового обзора. По оси абсцисс: радиус горла червоточины в единицах парсек/h, где h масштабный коэффициент Хаббла. Иллюстрация взята из [55]. Рис.4: Верхние границы доверительных вероятностей для плотности числа червоточин Эллиса во Вселенной (68% и 95%). Данные поиска квазаров Слоановского цифрового обзора. По оси абсцисс: радиус горла червоточины в единицах парсек/h, где h масштабный коэффициент Хаббла. Иллюстрация взята из [55].](http://personeltest.ru/aways/habrastorage.org/getpro/habr/upload_files/2f4/aa6/663/2f4aa66633d185d0bd7ca3ac19ed4b7b.jpg) Рис.4: Верхние границы доверительных
вероятностей для плотности числа червоточин Эллиса во Вселенной
(68% и 95%). Данные поиска квазаров Слоановского цифрового обзора.
По оси абсцисс: радиус горла червоточины в единицах парсек/h, где h
масштабный коэффициент Хаббла. Иллюстрация взята из [55].
Рис.4: Верхние границы доверительных
вероятностей для плотности числа червоточин Эллиса во Вселенной
(68% и 95%). Данные поиска квазаров Слоановского цифрового обзора.
По оси абсцисс: радиус горла червоточины в единицах парсек/h, где h
масштабный коэффициент Хаббла. Иллюстрация взята из [55]. Рис.5: Диаграмма Пенроуза для
червоточины, соединяющей две вселенные (раздел Вращающиеся звезды).
Рис.5: Диаграмма Пенроуза для
червоточины, соединяющей две вселенные (раздел Вращающиеся звезды).
 Рис.6: График ограничений на массу (ось
ординат, массы Солнца Mс) и радиуса перицентра rp (ось абсцисс,
2GMс) для гипотетической звезды, вращающейся вокруг Sgr A* с
обратной стороны червоточины и возмущающей орбиту S2 на нашей
стороне. Линии представляют собой ограничения с точностью ускорения
S2, равной 410^4 м/с*с, 210^5 м/с*с и 10^6 м/с*с соответственно.
Рис.6: График ограничений на массу (ось
ординат, массы Солнца Mс) и радиуса перицентра rp (ось абсцисс,
2GMс) для гипотетической звезды, вращающейся вокруг Sgr A* с
обратной стороны червоточины и возмущающей орбиту S2 на нашей
стороне. Линии представляют собой ограничения с точностью ускорения
S2, равной 410^4 м/с*с, 210^5 м/с*с и 10^6 м/с*с соответственно.
![Рис.7: Смоделированное изображение оптически тонкой области излучения для черной дыры Шварцшильда (слева) и проходимой сферически-симметричной червоточины (справа). Координаты осей абсцисс и ординат указаны в единицах гравитационного радиуса системы. Иллюстрация взята из [73]. Рис.7: Смоделированное изображение оптически тонкой области излучения для черной дыры Шварцшильда (слева) и проходимой сферически-симметричной червоточины (справа). Координаты осей абсцисс и ординат указаны в единицах гравитационного радиуса системы. Иллюстрация взята из [73].](http://personeltest.ru/aways/habrastorage.org/getpro/habr/upload_files/f19/4e9/f74/f194e9f74e80180f79ce91b15103bca3.jpg) Рис.7: Смоделированное изображение
оптически тонкой области излучения для черной дыры Шварцшильда
(слева) и проходимой сферически-симметричной червоточины (справа).
Координаты осей абсцисс и ординат указаны в единицах
гравитационного радиуса системы. Иллюстрация взята из
[73].
Рис.7: Смоделированное изображение
оптически тонкой области излучения для черной дыры Шварцшильда
(слева) и проходимой сферически-симметричной червоточины (справа).
Координаты осей абсцисс и ординат указаны в единицах
гравитационного радиуса системы. Иллюстрация взята из
[73].![Рис.8: Компактный объект с аккрецирующим геометрически тонким и оптически толстым диском. Иллюстрация взята из [89]. Рис.8: Компактный объект с аккрецирующим геометрически тонким и оптически толстым диском. Иллюстрация взята из [89].](http://personeltest.ru/aways/habrastorage.org/getpro/habr/upload_files/bc6/6d4/255/bc66d425524158e1eb60a4bf4528f2df.jpg) Рис.8: Компактный объект с аккрецирующим
геометрически тонким и оптически толстым диском. Иллюстрация взята
из [89].
Рис.8: Компактный объект с аккрецирующим
геометрически тонким и оптически толстым диском. Иллюстрация взята
из [89].
![Рис.9: Эволюция деформации, разделения черной дыры и ее относительной скорости для события GW150914 со временем. Иллюстрация взята из [15]. Рис.9: Эволюция деформации, разделения черной дыры и ее относительной скорости для события GW150914 со временем. Иллюстрация взята из [15].](http://personeltest.ru/aways/habrastorage.org/getpro/habr/upload_files/57b/8fc/4f7/57b8fc4f7fcbaac96914d7ef87be270c.jpg) Рис.9: Эволюция деформации, разделения
черной дыры и ее относительной скорости для события GW150914 со
временем. Иллюстрация взята из [15].
Рис.9: Эволюция деформации, разделения
черной дыры и ее относительной скорости для события GW150914 со
временем. Иллюстрация взята из [15].
 GN-z11 на фотографии обзора Great
Observatories Origins Deep Survey (GOODS).Credit: NASA, ESA, P.
Oesch (Yale University), G. Brammer (STScI), P. van Dokkum (Yale
University), and G. Illingworth (University of California, Santa
Cruz).
GN-z11 на фотографии обзора Great
Observatories Origins Deep Survey (GOODS).Credit: NASA, ESA, P.
Oesch (Yale University), G. Brammer (STScI), P. van Dokkum (Yale
University), and G. Illingworth (University of California, Santa
Cruz).
 Иллюстрация, показывающая историю
Вселенной сверху вниз: 1) Большой взрыв и ионизация (0-300 тыс
лет); 2) Темные века (300-500 000 тыс лет); 3) Конец Темных веков и
эпоха реионизации (500-1000 млн лет); 4) Существование Вселенной,
схожей с современной (1 млрд лет - настоящее время).Credit:
Djorgovski et al. (Caltech).
Иллюстрация, показывающая историю
Вселенной сверху вниз: 1) Большой взрыв и ионизация (0-300 тыс
лет); 2) Темные века (300-500 000 тыс лет); 3) Конец Темных веков и
эпоха реионизации (500-1000 млн лет); 4) Существование Вселенной,
схожей с современной (1 млрд лет - настоящее время).Credit:
Djorgovski et al. (Caltech).
 Реконструкция нити галактик: филаменты
(слева вверху), узлы соединения (справа вверху), наслоение (слева
внизу), воиды (справа внизу). По осям отмечены единицы SGX
(Supergalactic coordinates, англ: межгалактические
координаты)Credit: Sebastin E. Nuza
Реконструкция нити галактик: филаменты
(слева вверху), узлы соединения (справа вверху), наслоение (слева
внизу), воиды (справа внизу). По осям отмечены единицы SGX
(Supergalactic coordinates, англ: межгалактические
координаты)Credit: Sebastin E. Nuza
 РН Протон (слева) и РБ БризМ (справа спереди)
РН Протон (слева) и РБ БризМ (справа спереди)
 Эмиссионные линии спектра GN-z11.Credit: Jiang
et al.Цитата из источника (Jiang et al., arXiv.org: 2012.06936).
Эмиссионные линии спектра GN-z11.Credit: Jiang
et al.Цитата из источника (Jiang et al., arXiv.org: 2012.06936).
 Внешний
вид ELT без "обшивки"
Внешний
вид ELT без "обшивки"
 Roadmap разработки и фазы инструмента
Roadmap разработки и фазы инструмента
 Чрезвычайно большой телескоп (ELT)
Чрезвычайно большой телескоп (ELT)



























 Траектории частиц в двухщелевом эксперименте
Траектории частиц в двухщелевом эксперименте

 Стохастическое уравнение Ланжевена
воспроизводит плотности вероятности для осциллятора Морзе
Стохастическое уравнение Ланжевена
воспроизводит плотности вероятности для осциллятора Морзе































 Коробка
Коробка Комплектация прибора
Комплектация прибора Вид спереди
Вид спереди Вид
сбоку
Вид
сбоку Вид
сзади
Вид
сзади Режим "Монитор"
Режим "Монитор" Режим "Доза"
Режим "Доза" Режим "Поиск"
Режим "Поиск" Режим "Спектр"
Режим "Спектр" Начало
реакции прибора, 20см
Начало
реакции прибора, 20см Фон на
расстоянии 10см, 40мкР/ч
Фон на
расстоянии 10см, 40мкР/ч Фон на
расстоянии 5см, 130мкР/ч
Фон на
расстоянии 5см, 130мкР/ч Фон рядом с источником, Am-241, 0,8мкКи,
300мкР/ч
Фон рядом с источником, Am-241, 0,8мкКи,
300мкР/ч Фон рядом с источником, Ra-226, 740мкР/ч
Фон рядом с источником, Ra-226, 740мкР/ч Фон рядом с камерой Вильсона,
Pu-239-241. Am-241, 17мкР/ч
Фон рядом с камерой Вильсона,
Pu-239-241. Am-241, 17мкР/ч Фон от гранитного постамента, 70мкР/ч
Фон от гранитного постамента, 70мкР/ч Гамма-спектр Am-241
Гамма-спектр Am-241 Гамма-спектр Ra-226
Гамма-спектр Ra-226 Черника, Cs-137, спустя 10 часов
Черника, Cs-137, спустя 10 часов Черника, Cs-137. спустя 1 минуту
Черника, Cs-137. спустя 1 минуту
 "Главная"
"Главная" "Журнал"
"Журнал" "Настройки журнала", (Фото 1)
"Настройки журнала", (Фото 1) "Настройки журнала", (Фото 2)
"Настройки журнала", (Фото 2) "Спектр", наложение фона на спектр
"Спектр", наложение фона на спектр "Спектр", отображение разницы между фоном и
спектром
"Спектр", отображение разницы между фоном и
спектром "Спектр", отображение фона отключено
"Спектр", отображение фона отключено "Настройки спектра", (Фото 1)
"Настройки спектра", (Фото 1) "Настройки спектра", (Фото 2)
"Настройки спектра", (Фото 2) "Настройки спектра", (Фото 3)
"Настройки спектра", (Фото 3) "Калибровочные коэффициенты"
"Калибровочные коэффициенты" "Библиотека спектров"
"Библиотека спектров" "Панель быстрого доступа"
"Панель быстрого доступа" "Приборы"
"Приборы" "Настройки приложения", (Фото 1)
"Настройки приложения", (Фото 1) "Настройки приложения", (Фото 2)
"Настройки приложения", (Фото 2) "Экспертные настройки"
"Экспертные настройки" "Настройки прибора", (Фото 1)
"Настройки прибора", (Фото 1) "Настройки прибора", (Фото 2)
"Настройки прибора", (Фото 2) "Настройки прибора", (Фото 3)
"Настройки прибора", (Фото 3) "Карта"
"Карта" "Настройки
карты", (Фото 1)
"Настройки
карты", (Фото 1) "Настройки
карты", (Фото 2)
"Настройки
карты", (Фото 2) "Треки"
"Треки" Пример записанного трека
Пример записанного трека "Справка"
"Справка" "Сообщение разработчикам"
"Сообщение разработчикам" "О RadiaCode"
"О RadiaCode" "Графики"
"Графики" "Журнал"
"Журнал" "Спектр"
"Спектр"


























