Сравнение различных методов слияния двух отсортированных списков
Пусть у нас есть два списка (для простоты из целых чисел), каждый из которых отсортирован. Хотим объединить их в один список, который тоже должен быть отсортирован. Эта задача наверняка всем знакома, используется, например, при сортировке слиянием.
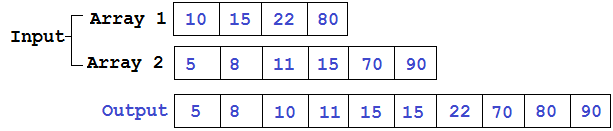
Способов реализации (особенно на python) достаточно много. Давайте разберем некоторые из них и сравним затачиваемое время на разных входных данных.
Основная идея алгоритма заключается в том, что, поместив по одной метке в начале каждого списка, будем сравнивать отмеченные элементы, брать меньший из них и передвигать метку в его списке на следующее число. Когда один из списков кончается, нужно добавить остаток второго в конец.
Входные данные не меняются
Пусть есть два списка list1 и
list2.
Начнем с самого простого алгоритма: обозначим метки за
i и j и будем брать меньший из
list1[i], list2[j] и увеличивать его
метку на единицу, пока одна из меток не выйдет за границу
списка.
При первом сравнении мы выберем минимальный элемент из двух минимальных в своем списке и подвинемся на следующий элемент, поэтому наименьший элемент из двух списков будет стоять на нулевом месте результирующего. Дальше несложно по индукции доказать, что далее слияние пройдет верно.
Перейдем к коду:
def simple_merge(list1, list2): i, j = 0, 0 res = [] while i < len(list1) and j < len(list2): if list1[i] < list2[j]: res.append(list1[i]) i += 1 else: res.append(list2[j]) j += 1 res += list1[i:] res += list2[j:] # один из list1[i:] и list2[j:] будет уже пустой, поэтому добавится только нужный остаток return res
Заметим, что в данном коде используется только перемещение вперед по списку. Поэтому будет достаточно работать с итераторами. Перепишем алгоритм с помощью итераторов.
Еще изменим обработку концов списков, так как теперь мы не умеем копировать сразу до конца. Будем обрабатывать элементы до того, когда оба итератора дойдут до конца, при этом, если один уже оказался в конце, будем просто брать из второго.
def iter_merge(list1, list2): result, it1, it2 = [], iter(list1), iter(list2) el1 = next(it1, None) el2 = next(it2, None) while el1 is not None or el2 is not None: if el1 is None or (el2 is not None and el2 < el1): result.append(el2) el2 = next(it2, None) else: result.append(el1) el1 = next(it1, None) return result
В этой реализации можно вместо добавления по одному элементу
(result.append()) собрать генератор, а потом из него
получить список. Для этого напишем отдельную функцию, которая будет
строить генератор, а основная функция сделает из него список.
def gen_merge_inner(it1, it2): el1 = next(it1, None) el2 = next(it2, None) while el1 is not None or el2 is not None: if el1 is None or (el2 is not None and el2 < el1): yield el2 el2 = next(it2, None) else: yield el1 el1 = next(it1, None)def gen_merge(list1, list2): return list(gen_merge_inner(iter(list1), iter(list2))) # из генератора получаем список
Встроенные реализации
Рассмотрим еще несколько способов слияния через встроенные в python функции.
-
mergeизheapq. Как говорит документация, эта функция делает именно то, что мы хотим, и больше: объединяет несколько итерируемых объекта, можно задать ключ, можно сортировать в обратном порядке.Тогда нам нужно просто импортировать и использовать:
from heapq import mergedef heapq_merge(list1, list2):return list(merge(list1, list2)) # тоже возвращает генератор
-
Counterизcollections.Counterумеет считать количество вхождений каждого из элементов, выдавать их в тех количествах, в которых они входят, и еще несколько полезных вещей, которые сейчас не нужны (например, несколько самых часто встречающихся элементов).Воспользуемся
gen_merge_innerдля слияния элементовCounter(list1)иCounter(list2):def counter_merge(list1, list2):return list(gen_merge_inner(Counter(list1).elements(), Counter(list2).elements()))
-
И, наконец, просто сортировка. Объединяем и сортируем заново.
def sort_merge(list1, list2):return sorted(list1 + list2)
Если можно менять исходные списки
Предположим, что после слияния старые списки больше не нужны
(как обычно и случается). Тогда можно написать еще один способ.
Будем как и раньше сравнивать нулевые элементы списков и вызывать
pop(0) у списка с меньшим, пока один из списков не
закончится.
def pop_merge(list1, list2): result = [] while list1 and list2: result.append((list1 if list1[0] < list2[0] else list2).pop(0)) return result + list1 + list2
Получили простенькую функцию на 4 строчки, но использовать дальше исходные списки не получится. Можно их скопировать, потом работать с копиями, но это потребует много дополнительного времени. Здесь будут проблемы с тем, что удаление нулевого элемента очень дорогое. Поэтому еще одна модификация будет заключаться в том, что мы будем вместо удаления из начала списка использовать удаление из конца, но придется в конце развернуть списки.
def reverse_pop_merge(list1, list2): result = [] while list1 and list2: result.append((list1 if list1[-1] > list2[-1] else list2).pop(-1)) return (result + list1[-1::-1] + list2[-1::-1])[-1::-1]
Сравнение
Пора перейти к самому интересному.
Составим список функций, которые будем сравнивать:
simple_mergeiter_mergegen_mergeheapq_mergecounter_mergesort_mergepop_mergereverse_pop_merge
Будем измерять время работы с помощью модуля
timeit. Код можно посмотреть здесь.
Разберем несколько ситуаций: оба списка примерно одинакового размера, один список большой, а второй маленький, количество вариантов элементов большое, количество вариантов маленькое. Кроме этого проведем просто общий случайный тест.
Тест первый
Проведем общий тест, размеры от до
, элементы от
до
.
Отдельно сравним pop и
reverse_pop:
pop_merge тратит колоссально больше времени в общем
случае, как и ожидалось.
Не будем учитывать здесь огромный pop_merge, чтобы
лучше видеть разницу между другими: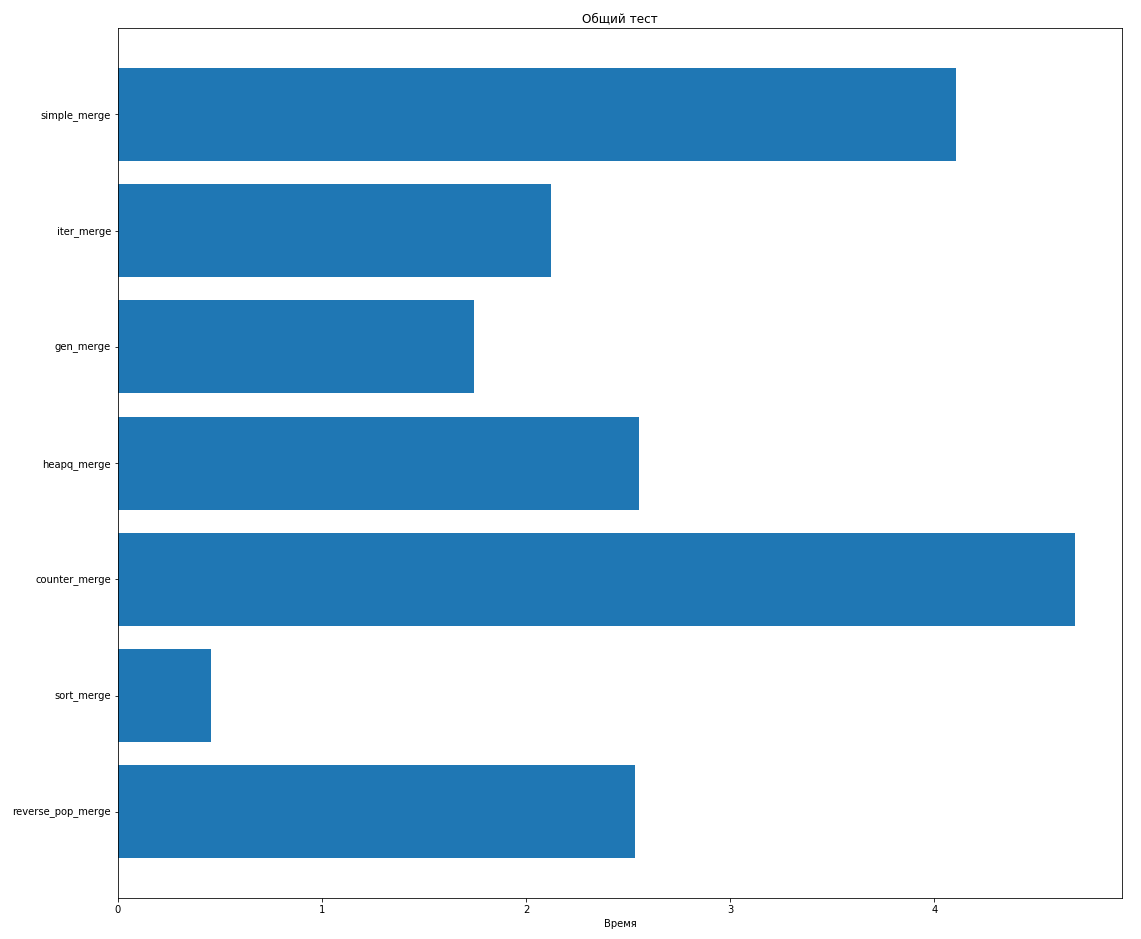
reverse_pop_merge показал себя относительно неплохо по
сравнению с ручной реализацией и heapq_merge.
Методы на итераторах работают еще быстрее, при этом видно, что получилось выгоднее построить генератор, чем добавлять элементы в список.
Тест второй, сравнимые размеры
Размеры будут принадлежать отрезку , а
увеличиваем, начиная с
. Шаг
.

Как уже можно видеть pop_merge при небольшом размере
списков еще ведет себя как heapq_merge, а дальше
обгоняет всех.
Тест третий, один маленький, второй большой
Размер первого равен , размер второго
.

В самом начале (на очень маленьких списках)
reverse_pop_merge обгоняет всех, кроме
sort_merge, но на чуть больших все выходит на
стандартные позиции.
Тест четвертый, много повторных
Размеры фиксированы, а количество элементов увеличивается на
, начиная с
.

Как видно, на достаточно малых количествах
counter_merge оказывается быстрее
reverse_pop_merge и heapq_merge, но потом
он отстает.
Итоги
Абсолютным победителем оказался sort_merge! Гораздо
быстрее просто отсортировать список заново, чем использовать вроде
бы линейные от длины списков функции.
На втором месте в подавляющем большинстве случаев идет
gen_merge, за ним следует iter_merge.
Остальные методы используют еще больше времени, но некоторые в каких-то крайних случаях достигают результатов 2-3 мест.
P.S.
Код, тесты, jupyter notebook c графиками можно найти на gitlab.
Возможно этот анализ неполон, буду рад добавить к сравнению ваши варианты, предлагайте.