Лекции по курсу Управление Техническими Системами, читает Козлов Олег Степанович на кафедре Ядерные реакторы и энергетические установки, факультета Энергомашиностроения МГТУ им. Н.Э. Баумана. За что ему огромная благодарность.
Данные лекции только готовятся к публикации в виде книги, а поскольку здесь есть специалисты по ТАУ, студенты и просто интересующиеся предметом, то любая критика приветствуется.
В предыдущих сериях:
1. Введение в теорию автоматического управления.
2. Математическое описание систем автоматического управления 2.1
2.3, 2.3 2.8, 2.9 2.13
В этом разделе мы будем изучать частотные характеристики, тема
сегодняшней статьи:
3.1. Амплитудно-фазовая частотная характеристика: годограф АФЧХ,
ЛАХ, ФЧХ
Будет интересно познавательно и жестко.

3.1. Амплитудно-фазовая частотная характеристика: годограф АФЧХ, ЛАХ, ФЧХ
Определение: Частотными характеристиками называются формулы и графики, характеризующие реакцию звена (системы) на единичное синусоидальное воздействие в установившемся режиме, т.е. в режиме вынужденных гармонических колебаний звена (системы).

Рис. 3.1.1 Схематическое представление синусаидального воздействия
Формула синусаидального воздействия может быть записана как:

Рисунок 3.1.2 График представления синусаидального воздействия
сдвиг фазы (не редконазывают
фаза);
амплитуда;
т.е. амплитуда на выходе звена(системы) и сдвиг фазы
зависят от частоты входного воздействия x(t).
Используем показательную форму записи функции единичного гармонического воздействия и отклика на это воздействие (рис. 3.1.1):
$$display$$\left \{ \begin{align} x(t)&= e^{i \cdot \omega \cdot t} = cos (\omega \cdot t) + i \cdot sin(\omega \cdot t)\\ y(t)&= A\cdot sin(\omega \cdot t+ \phi) \Rightarrow A \cdot e^{i(\omega \cdot t+\phi)}=A \cdot e^{i\cdot \omega \cdot t} \cdot e^{i \cdot\phi} = A(\omega) \cdot e^{i \cdot \omega \cdot t} \cdot e^{i \cdot \phi(\omega)} \end{align} \right.\ \ \ \ \ \mathbf{(3.1.1)} $$display$$
Определим связь между передаточной функцией и гармоничным
воздействием, пользуясь показательной формой.
Рассмотрим звено уравнение динамики которого имеет следующий
вид:
В показательной форме:
Передаточная функция:
Запишем в показательной форме используя
соотношения 3.1.1:
Подставим эти соотношения в (3.1.1) получим:
Поскольку (амплитуда на выходе звена(системы) и сдвиг фазы
зависят от частоты входного воздействия), то можно
записать:
если вспомнить, что в преобразования Лапаласа , то:
Получаем выражение для передаточной функции
Амплитудно-фазовая
частотная характеистика (АФЧХ)
Иногда называют частотной
передаточной функцией.
Модуль АФЧХ= тождественно
равен амплитуде выходного сигнала:
Сдвиг фазы выходного сигнала:
Обычно АФЧХ изображается на комплексной
плоскости. Формулы (3.1.6) и (3.1.7) позволяют изобразить
в полярных координатах
Так же можно изображать в традиционных декартовых
координатах:
Если использовать для представления W(s) форму W(s)=KN(s)/L(s), где L(s)- полиномы по степеням s, (причем свободные члены равны 1), а К общий коэффициент усиления звена (системы), то
Сдвиг фазы можно определить по виду
многочленов
и
(см. формулу (3.1.9))
т.е. как разность фаз (аргументов) числителя и знаменателя:
Постоим АФЧХ для абстрактного звена (системы) с передаточной функцией:
Подставляя в формулу различные значения

Рисунок 3.1.3 Годограф абстрактного звена.
Рассмотрим действительную и мнимую части полученных векторов Из рисунка 3.1.3 видно, что:
$$display$$\left \{ \begin{align} u( \omega)&= A( \omega) \cdot cos( \phi(\omega)) \\ v(\omega)&= A( \omega) \cdot sin( \phi(\omega)) \end{align} \right.$$display$$
Амплитуда и сдвиг фазы рассчитываются, для векторов
соответсвующих положительным частотам и лежащих в 4 квадранте
по
формулам:
$$display$$\left \{ \begin{align} A( \omega)&= \sqrt {u^2( \omega)+v^2( \omega)} ,\\ \phi(\omega)&= arctg \frac{v(\omega)}{u(\omega)} .\end{align} \right.$$display$$
В общем случае для любых углов сдвига, необходимо учитывать переход между квадрантами на плоскости, формула принимает вид:
где:
j = 0, 2, 3, 4..., если вектор в I и IV квадрант;
j = 1, 3, 4, 4..., если вектор в II и III квадранте.
Во всех технических системах отклик системы как правило отстает
от входного воздействия, то есть сдвиг фазы всегда отрицательный.
Исходя из формулы 3.1.10 степень полинома L(s) выше, чем полинома
N(s). Поскольку обычно степень полинома L(s) выше, чем полинома
N(s), то с увеличением частоты на входе в звено (в систему) сдвиг
фазы обычно отрицателен, т.е. сигнал на выходе звена еще больше
отстает по фазе от входного сигнала при увеличении частоты.
В предельном случае, если частота растет до бесконечности, мы можем
вообще не получить выходного воздействий. Обычно при величина
амплитуды на выходе звена стремится к 0, то есть lim A() = 0.
при замене
на
имеет зеркальное
изображение.
Анализируя годографы АФЧХ при > 0 (сплошная линия на рисунке
3.1.3) и при
< 0 (пунктирная линия) видим,
что:
четная функция,
следовательно график симметричен относительно оси ординат, а
нечетная функция
и ее график центрально-симметричен относительно начала
координат.

Рисунок 3.1.4 Зеркальная симметрия относительно оси ординат.

Рисунок 3.1.5 Центральная симметрия относительно начала координат.
Кроме анализа свойств звена (системы) по годографу АФЧХ широкое распространение получили анализ логарифмической амплитудной характеристики (ЛАХ) и фазочастотной характеристики (ФЧХ).
ЛАХ определяется как Lm()=20lgA().
Поскольку зачастую удобнее использовать десятичные логарифмы
(lg), чем натуральные(ln), в теории управления (также и в акустике)
значительно чаще используется специальная единица децибел (1/10
часть Бела):
+1Бел единица, характеризующая увеличение в 10 раз.
+1дБ (децибел) соответствует увеличению в раз.
В формуле Lm()=20lgA() величина Lm() измеряется также в
децибелах. Происхождение множителя 20 таково: A() амплитуда,
линейная величина, а мощность квадратичная величина (например,
напряжение в сети измеряется в Вольтах, а мощность () пропорциональна
квадрату напряжения, поэтому в формуле для Lm() стоит множитель 20
(чтобы привести ЛАХ (Lm()) к традиционной мощностной
характеристике).
Если больше
на 20 дБ, то это означает,
амплитуда
больше амплитуды
в 10 раз,
Окончательно: Lm()=20lgW(i)= 20lgA()
Из этого следует, что +1 децибел (+1 дБ) соответствует
увеличению амплитуды в раз (очень малая
величина); -1 дБ уменьшение амплитуды в
раз.
Графики A() и () имеют вид:

Рисунок 3.1.6 пример графика АЧХ

Рисунок 3.1.7 пример графика ФЧХ
Учитывая, что обычно изменяется на порядки и значение A() также на порядки, график Lm() строится, фактически, в логарифмических координатах, т.е. Lm() =Lm(lg()), например:

Рисунок 3.1.8 пример графика ЛАХ
Наклон ( 40 дБ/дек) соответствует уменьшению амплитуды в 100 раз при увеличении частоты в 10 раз.

Рисунок 3.1.9 пример графика ЛФЧХ
Рассмотренные характеристики Lm(), то есть ЛАХ и ФЧХ имеют широкое распространение при анализе динамических свойств звена (системы), например, при анализе устойчивости САР (см. раздел Устойчивость систем автоматического управления).

Рисунок 3.1.10 пример ЛАХ и ФЧХ для сложной системы
Пример 1
В качестве примера построим АФЧХ для демпфера, модель которого, разобрана в этой статье.... Добавим на схему блок Построение частотных характеристик качестве входа возьмем возмущающее воздействие, в качестве выхода положение положение груза. Для наглядности иллюстрации примем в качестве выхода положение в миллиметрах (х1000), поскольку модель у нас размерная и результат получается в метрах уже достаточно маленьким примерно 0.004 метра. см. рис. 3.11

Рисунок 3.1.11 Схема для построения частотных характеристик.
Параметры блока Построение частотных характеристик приведены на рисунке 3.1.12, для илюстации зависимости АЧХ и ЛАХ. Результат работы блока график с выбранными параметрам изображен на рисунке 3.1.13:

Рисунок 3.1.12 Парамеметры блока Частотные характеристики.

Рисунок 3.1.13 Частотные харатктеристики в АЧХ, ЛАХ, ФЧХ в линейном масштабе по .
Анализ графика в линейном масштабе по чаще всего не очень удобен, поскольку весь график собиается в узкой области, а дальше график абсолютной амплитуды практически сливается с 0. Если мы хотим исследовать частоты хотя бы до 1000 Гц, мы увидем практически вертикальные и горизонтальные прямые. Изменения масштаба шакалы АЧХ и на логарифмический позволяет более удобно исследовать частотные характеристики (см. рис. 3.1.14).
На рисунке 3.1.14 представлены частотные характеристики демпфера в логарифмическом масштабе и иллюстарция соотношения между абсолютной величиной амплитуды АФЧХ и ЛАХ в децибелах.

Рисунок 3.1.14 Частотные харатктеристики в АЧХ, ЛАХ, ФЧХ в логарифмитическом масштабе по .
Пример 2
Постоим частотные характеристики для чуть более сложной модели. А именно гидравлического демпфера рассмотренного в предыдущей лекции....
Для начала посмотрим модель в виде блоков.
Модель подготовленная для анализа представлена на рисунке
3.1.15. В отличие от исходной модели, описанной ранее, входное
воздействие задается блоком ступенька с скачком с 0 до 1 на 10
секунде расчтеа. В блоке линейная функции происходит пересчет
сигнала ступенька:
0 соответствует 200 бар в камере, (конечное состояние в предыдущем
примере),
1 соответствует 400 бар в камере.
Это сделано для того, что бы можно было подавать синусоидальный
сигнал и не получать отрицательное давление в камере плунжера. Так
же для наглядности графика, мы усиливаем выходное перемещение
переводя его из метров в миллиметры.

Рисунок 3.1.15 Модель гидравлического демпфера.
Частотные характеристики рассчитанные в конце рассчета приведены на рисунке 3.1.16. Видно что характеристики отличаются от простого пружинного демпфера сравните с 3.1.14

Рисунок 3.1.16 Частотные хараткеристики гидравлического депфера
Блок "Построение частотных характеристик" осуществляет расчет характеристик для линеаризованной модели, в окрестности заданной точки, это означает что частотные характеристики системы в разные моменты времени могут отличатся для нелинейных моделей. Например в нашем случае характеристики в начале рассчета будут отличатся от характеристик полученных в конце рассчета.
Для подробных и нелинейных моделей, блок Построение частотных характеристик, может не работать из за наличия разрывов и нелинейностей в модели. Например для точной модели демпфера, которую мы проверяли в предыдущей статье. В этом случае возможно построить частотные характеристики непосредственно моделированием, путем подачи синусоидального сигнала с разной частотой и измерения отклика. В SimInTech для этого используется блок Гармонический анализатор, который подключается к входу модели и генерирует синусоидальной воздействие, в этот же блок направляется отклик системы и производится вычисление необходимых параметров для построения различных характеристик системы, которые можно вывести на графики с помощью блока фазовый портрет.
Модель гидравлического демпфера собранного из библиотечных блоков SimInTech представлена на рисунке 3.1.7

Рисунок 3.1.17 Модель гидравлическогго демпфера для рассчета частотных характеристик.
Расчеты с моделью показывают, что при сохранении общего вида графиков, значения полученные при для подробной модели отличаются от линеаризованной модели, (см. рис. 3.18 3.19)

Рисунок 3.1.18 АЧХ подробной модели привода, полученная прямым моделированием.

Рисунок 3.1.19 ЛАХ подробной модели привода, полученная прямым моделированием.
Использование прямого моделирования, для получения характеристик, является более надежным способом и работает не только с линейными моделями, но может быть использован для построения характеристик некоторых реальных объектов, если их можно подключить к среде моделирования и воздействовать в реальном режиме времени. Однако затраты на вычисления значительно больше. Например для получения характеристик демпфера пришлось выполнить процесса 40 000 секунд модельного времени, на обычном компьютере это заняло порядка 35 минут. График процесса перемещения плунжера в процессе вычисления характеристик приведен на рисунке 3.1.20.

Рисунок 3.1.20 Перемещения плунжера в процессем моделирования.
Блок Гармонический анализаторимеет выходы:
Re(w*t) текущее значение действительной части амплитудно-фазовой
частотной характеристики исследуемой системы;
Im(w*t) текущее значение мнимой части амплитудно-фазовой частотной
характеристики.
Это позволяет построить годограф исследуемой системы с помощью
фазового портрета. (см. рис. 3.1.21)

Рисунок 3.1.21 Годограф системы гидравличесого демпфера.
Модели, использованные для илюстарции в лекции можно взять здесь...
Продолжение следует.
 Рисунок 3.3.1 Расчетная схема камеры смешения
Рисунок 3.3.1 Расчетная схема камеры смешения
 Рисунок 3.3.2 Годограф АФЧХ
апериодического звена 1-го порядка
Рисунок 3.3.2 Годограф АФЧХ
апериодического звена 1-го порядка
 Рисунок 3.3.3 АЧХ апериодического звена 1-го
порядка
Рисунок 3.3.3 АЧХ апериодического звена 1-го
порядка Рисунок 3.3.4 ФЧХ апериодического звена 1-го порядка
Рисунок 3.3.4 ФЧХ апериодического звена 1-го порядка
 Рисунок 3.3.5 ЛАХ и ЛФЧХ апериодического
звена 1-го порядка
Рисунок 3.3.5 ЛАХ и ЛФЧХ апериодического
звена 1-го порядка
 Рис.3.3.6 Переходная функция
апериодического звена 1-го порядка
Рис.3.3.6 Переходная функция
апериодического звена 1-го порядка Рис.3.3.7 Весовая функция апериодического
звена 1-го порядка
Рис.3.3.7 Весовая функция апериодического
звена 1-го порядка
 Рисунок 3.3.8 Примеры апериодических
звеньев 1-го порядка
Рисунок 3.3.8 Примеры апериодических
звеньев 1-го порядка
 Рисунок 3.3.9 Частотный анализ модели
камеры смешения в виде стандартного апериодического звена
Рисунок 3.3.9 Частотный анализ модели
камеры смешения в виде стандартного апериодического звена
 Рисунок 3.3.10 Годограф модели камеры
смешения в виде Инерционного звена первого порядка.
Рисунок 3.3.10 Годограф модели камеры
смешения в виде Инерционного звена первого порядка.
 Рисунок 3.3.11 Модель камеры смешения в коде НS.
Рисунок 3.3.11 Модель камеры смешения в коде НS.
 Рисунок 3.3.12 Температура в узле в
начальный период расчета.
Рисунок 3.3.12 Температура в узле в
начальный период расчета.
 Рисунок 3.3.13 Настройка файлов рестартов.
Рисунок 3.3.13 Настройка файлов рестартов.
 Рисунок 3.3.13 Пакет для сравнения
моделей узла смешения.
Рисунок 3.3.13 Пакет для сравнения
моделей узла смешения.
 Рисунок 3.3.14 Сравнение переходного
процесса для разных моделей камеры смешения.
Рисунок 3.3.14 Сравнение переходного
процесса для разных моделей камеры смешения.
 Рисунок 3.3.15 Колебания давления и
расхода при ступенчатом изменении температуры.
Рисунок 3.3.15 Колебания давления и
расхода при ступенчатом изменении температуры.
 Рисунок 3.3.16 Модель частотного анализа
внешней системы.
Рисунок 3.3.16 Модель частотного анализа
внешней системы.
 Рисунок 3.3.17 Скрипт гидравлической модели.
Рисунок 3.3.17 Скрипт гидравлической модели.
 Рисунок 3.3.18. Результаты анализа
частотного анализа гидравлической модели.
Рисунок 3.3.18. Результаты анализа
частотного анализа гидравлической модели.
 Рисунок 3.3.19 Давление в узле и расход в
выходном канале с ростом частоты воздействия по температуре.
Рисунок 3.3.19 Давление в узле и расход в
выходном канале с ростом частоты воздействия по температуре.
 Рисунок 3.5.1 Модель электического
колебательного контура
Рисунок 3.5.1 Модель электического
колебательного контура
 Рисунок 3.5.2 АЧХ колебательного звена
Рисунок 3.5.2 АЧХ колебательного звена Рисунок 3.5.3 ФЧХ колебательного звена
Рисунок 3.5.3 ФЧХ колебательного звена
 Рисунок 3.5.4 АФЧХ колебательного звена
Рисунок 3.5.4 АФЧХ колебательного звена Рисунок 3.5.5 Годограф АФЧХ консервативного звена
Рисунок 3.5.5 Годограф АФЧХ консервативного звена
 Рисунок 3.5.6 ЛАХ колебательного звена
Рисунок 3.5.6 ЛАХ колебательного звена
 Рисунок 3.5.6 Переходная функция консервативного
звена
Рисунок 3.5.6 Переходная функция консервативного
звена
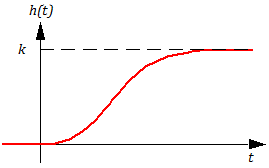 Рисунок 3.5.8 Переходная функция
колебательного звена (при = 1)
Рисунок 3.5.8 Переходная функция
колебательного звена (при = 1) Рисунок 3.5.9 Переходная функция
колебательного звена (при 0 < < 1)
Рисунок 3.5.9 Переходная функция
колебательного звена (при 0 < < 1)
 Рисунок 3.5.10 Весовая функция
колебательного звена при = 0.
Рисунок 3.5.10 Весовая функция
колебательного звена при = 0.
 Рисунок 3.5.11 Весовая функция
колебательного звена при = 1.
Рисунок 3.5.11 Весовая функция
колебательного звена при = 1.
 Рисунок 3.5.12 Весовая функция
колебательного звена при 0 < < 1.
Рисунок 3.5.12 Весовая функция
колебательного звена при 0 < < 1.
 Рисунок 3.5.13 Модель колебательного контура
Рисунок 3.5.13 Модель колебательного контура
 Рисунок 3.5.14 Общие сигналы проекта.
Рисунок 3.5.14 Общие сигналы проекта. Рисунок 3.5.15. Вычисление параметров для
колебательного звена.
Рисунок 3.5.15. Вычисление параметров для
колебательного звена.
 Рисунок 3.5.16. Графики напряжений
источника и на конденсаторе.
Рисунок 3.5.16. Графики напряжений
источника и на конденсаторе.
 Рисунок 3.5.17 Сравнение модели контура и
колебательного звена
Рисунок 3.5.17 Сравнение модели контура и
колебательного звена
 Рисунок 3.5.18. Частотный анализ
электрического контура
Рисунок 3.5.18. Частотный анализ
электрического контура
 Рисунок 3.5.19 Результаты гармонического анализа.
Рисунок 3.5.19 Результаты гармонического анализа.
 Рисунок 3.5.20 Модель с изменяемыми
параметрами контура.
Рисунок 3.5.20 Модель с изменяемыми
параметрами контура.
 Рисунок 3.5.21. Скрипт изменения параметров модели
Рисунок 3.5.21. Скрипт изменения параметров модели
 Рисунок 3.5.22. Настройки контура для
устранения колебаний
Рисунок 3.5.22. Настройки контура для
устранения колебаний Рисунок 3.5.23. Графики изменения
переходных процессов в контуре при изменении R и С.
Рисунок 3.5.23. Графики изменения
переходных процессов в контуре при изменении R и С.
 Рисунок 3.5.24 Схема колебательного
контура с настройками частоты источника.
Рисунок 3.5.24 Схема колебательного
контура с настройками частоты источника.
 Рисунок 3.5.24 Скрипт для управления и
отображения частоты.
Рисунок 3.5.24 Скрипт для управления и
отображения частоты.
