Wolfram mathematica

Циркулярные кривые 2-го порядка

01.09.2020 20:19:15 |

Автор: admin

Как известно, кривыми Безье нельзя построить дугу окружности или эллипса. В этой статье рассматриваются кривые, лишённые такого недостатка.

Кривые Безье

Логика построения кривых Безье хорошо понятна из следующей анимации:

Чтобы получить формулу непосредственно из графического представления, достаточно определить вспомогательную функцию для линейной интерполяции между двумя точками, в которая при изменении параметра t от 0 до 1 возвращает промежуточные значения от a до b:

$display$

Примечание

В математике как-то не сложилось устойчивого названия для функции линейной интерполяции и в зависимости от сферы применения она может называться lerp, blend, mix и как-то ещё. К ней также относится и кривая Безье первого порядка.

С её помощью можно последовательно найти необходимые точки сначала найти

$display$

а затем уже через них найти

$display$

При желании, можно подставить функции друг в друга и сократить хотя это особо и не упростит вычисления, зато позволит обобщить кривые на произвольное количество опорных точек (через полиномы Бернштейна). В нашем случае получим

$display$

Увеличение порядка кривых достигается тривиально исходные точки задаются не константно, а как результат интерполяции между n+1 других контрольных точек:

Примечание

В этих формулах в качестве точек могут выступать как комплексные числа, так и векторы произвольной размерности. Дальнейшие формулы будут корректными только для комплексных чисел.

Циркулярные кривые

Дуга окружности

Чтобы похожим образом построить дугу окружности, необходимо определить соответствующую логику построения по аналогии с черчением окружности циркулем.

Изначально нам неизвестен центр окружности d он находится через пересечение перпендикуляров к касательным в точках a и b (далее узловых); сами же касательные задаются с помощью точки c (далее направляющей). Для построения произвольной дуги окружности (меньшей 180) достаточно, чтобы расстояния от направляющей точки до узловых были одинаковыми.

Дуга эллипса

Построить дугу эллипса уже посложнее потребуется два вектора, вращающихся в разные стороны (подробнее здесь)

Используя озвученный выше способ нахождения точки d, мы уже не можем построить произвольную дугу эллипса только лишь от 0 до 90 (в том числе и повёрнутую на некоторый угол).

Дуга гипотрохоиды

Задав условие, что в начале и конце черчения векторы должны лежать на одной прямой, мы получим дугу гипотрохоиды во всех остальных случаях. Это условие не случайно и (помимо однозначного определения кривой) гарантирует совпадение касательных в узловых точках. Как следствие, угловые пути, которые проходят оба вектора, станут разными, но в сумме по-прежнему будут давать 180.

Как изменяется форма кривой в зависимости от положения направляющей точки, можно посмотреть на следующей анимации:

Алгоритм

Поскольку здесь мы имеем вращения на двумерной плоскости, математику построения этих кривых удобно описывать через комплексные числа.

1) находим точку пересечения нормалей касательных, проведённых от направляющей точки к узловым:

$d=\frac{(2 a-c) (c-b) a^*+ (2 b-c) (a-c) b^*-c (a-b) c^*}{(c-b)a^*+(a-c) b^*-(a-b) c^*}$

(здесь звёздочка означает комплексное сопряжение).

2) зная d, находим длины нормалей

$r_{\text{ad}}=\left| a-d\right|$

$r_{\text{bd}}=\left| b-d\right|$

и их сумму и разность

$r_m=\frac{1}{2} \left(r_{\text{ad}}+r_{\text{bd}}\right)$

$r_s=\frac{1}{2} \left(r_{\text{ad}}-r_{\text{bd}}\right)$

3) находим единичный вектор, от которого начинается построение

$v=\frac{a-d}{\left| a-d\right| }$

Примечание

в некоторых библиотеках для работы с комплексными числами и системах компьютерной алгебры для этого есть отдельная функция sign(x).

4) находим угловые пути, которые должны пройти каждый из векторов

$\phi _m=\arg \left(\frac{a-d}{b-d}\right)$

$\phi _s=\arg \left(-\frac{a-d}{b-d}\right)$

Примечание

При умножении векторов их длины умножаются, а углы складываются. Здесь деление используется для противоположной задачи найти разницу углов, т. е. угол между векторами.

Поскольку для функции аргумента длина вектора не играет роли, тот же результат можно получить и заменив деление умножением на комплексно сопряжённый вектор такой вариант даже предпочтительнее, поскольку будет более численно устойчив на очень малых значениях из-за отсутствия деления; здесь же выбор в пользу деления сделан исключительно ради наглядности.

Здесь имеется ещё один крайне важный момент. Если бы мы сначала нашли углы для каждого вектора по отдельности, а потом бы считали разницу как

$\arg (a-d)-\arg (b-d)$

результат не всегда был бы корректным из-за многозначности функции аргумента.

5) последовательно изменяя t от 0 до 1 с некоторым шагом, находим принадлежащую кривой точку по формуле

$d+v \left(r_m e^{-i t \phi _m}+r_s e^{-i t \phi _s}\right)$

Циркулярные сплайны

Так же, как и кривые Безье, эти кривые можно совмещать для кусочно-непрерывного построения сплайнов. Для обеспечения гладкости в узловых точках (стыковки) необходимо, чтобы узловая точка находилась на одной линии с двумя соседними направляющими точками. Для этого можно задавать узловые точки не явным образом, а через интерполяцию направляющих точек. Их также можно не задавать вообще, вычисляя полностью автоматически например, как среднее между направляющих точек:

Справа для сравнения использован тот же подход с кривыми Безье 2-го порядка.

Замечания и нюансы

В отличие от кривых Безье, здесь кривая не всегда лежит внутри фигуры из линий, соединяющих контрольные точки, например

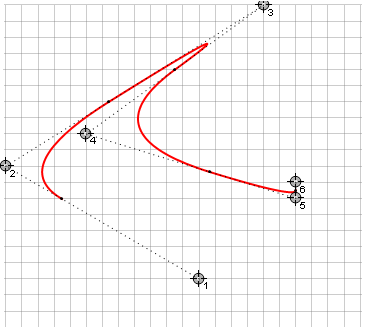
Кроме того, существует вырожденный случай, который необходимо обрабатывать отдельно когда направляющая точка лежит на одной прямой с узловыми точками. При этом кривая вырождается в прямую, а при попытке вычислить точку d возникает деление на ноль.

У этих кривых также имеется ограничения на кривизну линии, поскольку в соответствии с алгоритмом выбирается наименьший путь следования и кривая не может обогнуть больше, чем 180. Это приводит к тому, что при кусочно-непрерывной интерполяции могут возникать острые углы при определённом положении направляющих точек (справа те же точки для Безье):

Заключение

Дальнейшим развитием рассмотренного метода построения кривых является увеличение количества векторов, участвующих в построении кривой и, соответственно, увеличение количества направляющих точек. Однако, в отличие от кривых Безье, повышение порядка здесь не является очевидным и требует отдельного вдумчивого размышления. Также возможны различные методы комбинации их с кривыми Безье в частности, интерполяции центра окружности рисующих векторов.

Рассмотренный метод построения кривых также не является единственным, частным случаем которого являются дуги окружности и эллипса как минимум, эллипс можно построить через пересечение прямых в параллелограмме (правда, в этом варианте автор потерпел неудачу). Возможно, что существуют и другие решения, в том числе и варианты описанного в статье пишите в комментариях, если вам что-то известно на эту тему.

Исходный код статьи можно скачать на GitHub.

Подробнее..

Категории: Алгоритмы , Математика , Кривые , Интерполяция , Безье , Сплайны , Комплексные числа , Wolfram mathematica

Как нарисовать звезду (и не только) в полярных координатах

22.09.2020 08:08:59 |

Автор: admin

Вопрос о формуле для многоугольника в полярных координатах регулярно возникает на тематических ресурсах и так же регулярно остаётся без внятного ответа. В лучшем случае попадается решение через функцию остатка от деления что не является чистым с математической точки зрения, поскольку не позволяет производить над функцией аналитические преобразования. Видимо, настоящие математики слишком заняты решением проблем тысячелетия и поисками простого доказательства теоремы Ферма, чтобы обращать внимание на подобные банальные задачи. К счастью, в этом вопросе воображение важнее знания, и для решения этой задачи не нужно быть профессором топологических наук достаточно знания школьного уровня.

Формула для равностороннего многоугольника в полярных координатах выглядит очень просто

$\rho = \frac{\cos \left(\frac{2 \sin ^{-1}(k)+\pi m}{2 n}\right)}{\cos \left(\frac{2 \sin ^{-1}(k \cos (n \phi ))+\pi m}{2 n}\right)}$

и имеет следующие параметры:

$\phi$ угол;
$inline$ количество выпуклых вершин;
$inline$ определяет, через какое количество вершин стороны будут лежать на одной прямой. Для него допустимы и отрицательные значения от знака будет зависеть, в какую сторону будет выгибаться звезда;
$inline$ жёсткость при $inline$ мы получим окружность вне зависимости от прочих параметров, при $inline$ многоугольник с прямыми линиями, при промежуточных значениях от $inline$ до $inline$ промежуточные фигуры между окружностью и многоугольником.

С этой формулой можно нарисовать звезду двумя путями:

1) $inline$

2) $inline$ . В этом случае требуется сделать два оборота вместо одного:

Параметр $inline$ влияет на многоугольник следующим образом (здесь он изменяется от -1 до 5):

Параметр $inline$ в анимации:

Комплексная форма и модификации

Можно переписать исходную формулу в комплексном виде, и, несмотря на наличие в ней мнимых единиц, значение радиуса по-прежнему будет оставаться действительным:

$\rho = \frac{4^{1/n} \left(\sqrt{1-k^2}+i k\right)^{-1/n} \left(1+\left(\sqrt{1-k^2}+i k\right)^{2/n} e^{\frac{i \pi m}{n}}\right) \left(\sqrt{1-k^2 \cos ^2(n \phi )}+i k \cos (n \phi )\right)^{1/n}}{4^{1/n}+e^{\frac{i \pi m}{n}} \left(2 \sqrt{1-k^2 \cos ^2(n \phi )}+2 i k \cos (n \phi )\right)^{2/n}}$

На первый взгляд это может показаться бессмысленным, поскольку формула стала чуть более громоздкой но не стоит спешить с выводами. Во-первых, в ней отсутствует арксинус, что полностью меняет математический смысл формулы и позволяет по-другому посмотреть на построение звёздчатого многоугольника. Во-вторых, из неё также можно получить компактные формулы для частных случаев, например $\frac{i^t \left(i^{n t}\right)^{1/n}}{1+\left(i^{n t}\right)^{2/n}}$ . В-третьих (и самое интересное), её можно творчески модифицировать и получать другие, неожиданные формы. Для того, чтобы появление возможной мнимой компоненты в радиусе не вызывало неоднозначности при вычислении, можно её сразу привести к декартовым координатам умножением на $e^{i \phi }$ . Вот примеры некоторых модификаций:

$\frac{(-1)^{2/3} e^{i \phi } \sqrt[3]{\sqrt{\sin ^2(3 \phi )}+i \cos (3 \phi )}}{(-1)^{2/3}+2^{2/3} \left(\sqrt{\sin ^2(3 \phi )}+i \cos (3 \phi )\right)^{2/3}}$

$\frac{e^{i \phi } \sqrt{\sqrt{\sin ^2(2 \phi )}+i \cos (2 \phi )}}{\sqrt{2} \left(\sqrt{\sin ^2(2 \phi )}+i \cos (2 \phi )\right)^{3/2}+e^{i/2}}$

$\frac{e^{\frac{1}{4} i (4 \phi +\pi )}}{2 \sqrt{\sqrt{\sin ^2(2 \phi )}+\sqrt[4]{-1} \cos (2 \phi )}+(-1-i)}$

Как вы наверняка заметили, вращение вектора перестало быть равномерным и именно из-за появления мнимой составляющей в радиусе.

Квадрокруги и прочее

У нашей формулы есть замечательный частный случай квадрат, формулу для которого можно выписать как

$\rho = \frac{2}{\sqrt{2+\sqrt{2+2 \cos (4 \phi )}}}$

или

$\rho = \sqrt{\frac{2}{1+\sqrt{1-\sin ^2(2 \phi )}}}$

(выбирайте, какая больше нравится).

В чуть более развёрнутом случае можно определить промежуточные фигуры между кругом и квадратом через точку $inline$ на плоскости

$\rho = \sqrt{\frac{2}{1+\sqrt{1-\frac{\left(2 k^2-1\right) \sin ^2(2 \phi )}{k^4}}}}$

Можно также добавить вариативности этим фигурам с сохранением условия прохождения их через точку $inline$ модулируя непосредственно сам параметр $inline$ в зависимости от угла таким образом, чтобы при прохождении через диагонали его множитель был равен единице. Например, подставив вместо $inline$ функцию $\frac{k}{1-z \cos ^2(2 \phi )}$ , мы получим дополнительный параметр $inline$ , которым можно регулировать дополнительные изгибы. В частности, для $inline$ получится следующее:

В ещё более развёрнутом случае можно определить не просто квадрат а прямоугольник, и по прежнему в полярных координатах:

$\rho = \sqrt{\frac{4 a^2 b^2}{\left(\left(b^2-a^2\right) \cos (2 \phi )+a^2+b^2\right) \left(\sqrt{1-\frac{4 a^2 b^2 k \sin ^2(2 \phi )}{\left(\left(b^2-a^2\right) \cos (2 \phi )+a^2+b^2\right)^2}}+1\right)}}$

И даже посчитать его площадь (через эллиптические интегралы):

$S=4 a b\frac{((k-1) K(k)+E(k))}{k}$

Примечание

Для крайних значений $inline$ ( $inline$ и $inline$ ) эта функция имеет особые точки, которые можно посчитать через предел и они ожидаемо будут равны $\pi a b$ и $inline$ .

Это позволит делать профили с переходом из окружности в прямоугольник с контролируемой площадью сечения. Здесь площадь константна:

А здесь площадь расширяется по экспоненциальному закону:

Переход к декартовым координатам

Любую формулу в полярных координатах можно выразить через уравнение в декартовых координатах, причём как минимум двумя способами в зависимости от чего будет изменяться вид градиента на границе фигуры. Для этого достаточно посчитать угол через арктангенс от координат и привести формулу к константе через радиус-вектор вычитанием

$0=\sqrt{x^2+y^2}-\frac{\cos \left(\frac{2 \sin ^{-1}(k)+\pi m}{2 n}\right)}{\cos \left(\frac{2 \sin ^{-1}\left(k \cos \left(n \tan ^{-1}(x,y)\right)\right)+\pi m}{2 n}\right)}$

или делением

$1=\frac{\sqrt{x^2+y^2} \cos \left(\frac{2 \sin ^{-1}\left(k \cos \left(n \tan ^{-1}(x,y)\right)\right)+\pi m}{2 n}\right)}{\cos \left(\frac{2 \sin ^{-1}(k)+\pi m}{2 n}\right)}$

Второй вариант предпочтительнее, поскольку даёт прямые градиенты вдоль сторон многоугольника.

Примечание

Здесь также нужно помнить, что в точке (0,0) возникает неопределенность из-за деления на ноль которая, впрочем, легко разрешается через предел (который будет равным $-\cos \left(\frac{2 \sin ^{-1}(k)+\pi m}{2 n}\right) \sec \left(\frac{2 \sin ^{-1}\left(k \cos \left(\frac{\pi n}{2}\right)\right)+\pi m}{2 n}\right)$ в первом случае и нулю во втором).

Выражение $\cos \left(n \tan ^{-1}(x,y)\right)$ также можно упростить до $\frac{(x+i y)^n+(x-i y)^n}{2 \left(x^2+y^2\right)^{n/2}}$ , коэффициенты числителя которого при разложении образуют знакочередующий вариант последовательности A034839.

Значение формулы из правой части уравнения (во 2-м случае) будет меняться от $inline$ до $inline$ если точка $inline$ попадает внутрь фигуры, и от $inline$ до бесконечности если нет. Выбирая различные функции для преобразования её в яркость, можно получать различные варианты растеризации. Для экспоненты ( $e^{-x-1}$ для первого и $e^{-x}$ для второго варианта) получим

или, если с насыщением

Можно использовать классический фильтр нижних частот $\frac{1}{x^p+1}$ , в котором $inline$ порядок фильтра, определяющий степень затухания.

Для первого варианта:

И для второго:

Можно использовать и кусочно-непрерывную функцию, явно задавая границы интерполяции.

Помимо растеризации как таковой, можно задавать и деформации например, сжать шахматную доску в круг:

Или даже натянуть её на сферу:

формула

$x=\frac{u}{\sqrt{\frac{2}{1+ \left| \frac{u^2-v^2}{u^2+v^2} \right|}}}$

$y=\frac{v}{\sqrt{1+\frac{2}{\left| \frac{u^2-v^2}{u^2+v^2}\right| }}}$

$z=\sqrt{1-\frac{1}{2} u^2 \left(1+\left| \frac{u^2-v^2}{u^2+v^2}\right|\right)-\frac{1}{2} v^2 \left(1+\left| \frac{u^2-v^2}{u^2+v^2}\right|\right)}$

Appendix: как была получена формула

Классический стиль повествования в математических текстах состоит из чередования лемм/теорем и их доказательств как если бы доказуемые утверждения появлялись у авторов в голове откровением свыше. И хотя в этом и бывает доля истины, чаще появлению формул предшествует некоторая исследовательская работа, описание которой может дать большее понимание их смысла, чем формальное доказательство; а верность утверждений, в свою очередь, можно проследить через верность шагов, к ним приведших.

Так и здесь если бы статья началась с формулы в комплексной форме, то её появление было бы неочевидным и контр-интуитивным, а заявленные свойства требовали бы дополнительных доказательств. Но в тригонометрической форме записи историю её появления вполне возможно проследить.

1) начинаем с самого простого случая задаче начертить прямую в полярных координатах. Для этого нужно решить уравнение $r \cos (\phi )=1$ , решение которого очевидно $r\to \sec (\phi )$ .

2) далее аргумент секанса нужно зациклить, чтобы обеспечить изломы в прямой. Именно на этом этапе другие решения используют грязный хак в виде остатка от деления. Здесь же используется последовательное взятие прямой и обратной функции синуса $\sin ^{-1}(\sin (\phi ))$

Такой подход позволяет производить стандартные математические операции над получившейся формулой,

например

можно её продифференцировать и получить функцию для прямоугольной волны:

$\frac{\partial \sin ^{-1}(\sin (\phi ))}{\partial \phi }=\frac{\cos (\phi )}{\sqrt{1-\sin ^2(\phi )}}$

Благодаря этой же записи можно упростить функцию квадрата в полярных координатах до более эстетического вида, используя представление тригонометрический функций в комплексном виде. В Wolfram Mathematica это можно сделать с помощью функций TrigToExp и ExpToTrig:

код

Sec[1/2 ArcSin[k Sin[2
\[Phi]]]]^2//TrigToExp//ExpToTrig//Sqrt[#]&//FullSimplify

$\frac{2}{\sqrt{2+2 \sqrt{1-k^2 \sin ^2(2 \phi )}}}$

Благодаря этой же записи можно получить гладкие промежуточные фигуры между кругом и квадратом с помощью дополнительного множителя $inline$ , благодаря которому аргумент арксинуса не дотягивает до единицы $\sin ^{-1}(k \sin (\phi ))$ :

А для того, чтобы функция пересекала заданную точку, нужно просто составить уравнение и пересчитать $inline$ :

$\sqrt{\frac{2}{1+\sqrt{1-k' \sin ^2( \frac{\pi}{2} )}}}=k$

код

Solve[(Sqrt[2/(1+Sqrt[1-k Sin[2
\[Phi]]^2])] /. \[Phi]->Pi/4)==x, k] /. x->k

$k'\to \frac{4 \left(k^2-1\right)}{k^4}$

3) параметры $inline$ и $inline$ были просто добавлены творческим способом и их влияние исследовалось экспериментально, по факту.

4) Прямоугольник легко получить перейдя к параметрическому виду и растягиванием осей

$x=a \cos (t) \sqrt{\frac{2}{1+\sqrt{1-\sin ^2(2 t)}}}$

$y=b \sin (t) \sqrt{\frac{2}{1+\sqrt{1-\sin ^2(2 t)}}}$

Но после этого $inline$ уже не будет значить угол, теперь $inline$ это просто параметр, который описывает вектор через его проекции на координатные оси. Чтобы перейти обратно к полярным координатам нужно найти длину вектора (через корень суммы квадратов), угол (через арктангенс отношения), выразить этот угол через $\phi$ и подставить получившееся выражение вместо $inline$ .

код

With[{r = Sqrt[2/(1 + Sqrt[

1 - Sin[2 t]^2])]}, {Sqrt[(a r Cos[t])^2 + (b r Sin[t])^2],

ArcTan[(b r Sin[t])/(a r Cos[t])]}] // Simplify

$\left\{\sqrt{2} \sqrt{\frac{a^2 \cos ^2(t)+b^2 \sin ^2(t)}{\sqrt{\cos ^2(2 t)}+1}},\tan ^{-1}\left(\frac{b \tan (t)}{a}\right)\right\}$

Solve[ArcTan[(b Tan[t])/a]==\[Phi], t]

$t\to \tan ^{-1}\left(\frac{a \tan (\phi )}{b}\right)$

Sqrt[2] Sqrt[(a^2 Cos[t]^2 + b^2 Sin[t]^2)/(1 + Sqrt[Cos[2
t]^2])]

/. t -> ArcTan[(a Tan[\[Phi]])/b] // Simplify

$\sqrt{2} \sqrt{\frac{a^2 b^2 \sec ^2(\phi )}{\left(a^2 \tan ^2(\phi )+b^2\right) \left(\sqrt{\cos ^2\left(2 \tan ^{-1}\left(\frac{a \tan (\phi )}{b}\right)\right)}+1\right)}}$

Упростить такую формулу уже посложнее, и для этого потребуется несколько этапов:

1) перейти к декартовым координатам заменой $\phi \to \tan ^{-1}(x,y)$ ;
2) перейти к экспоненциальному виду;
3) упростить;
4) сделать обратную замену $x\to \cos (\phi )$ и $y\to \sin (\phi )$ ;
5) опять перейти к экспоненциальному виду;
6) упростить.

В результате получим такую формулу:

код

Sqrt[2] Sqrt[(a^2 b^2
Sec[\[Phi]]^2) /

((1 + Sqrt[Cos[2 ArcTan[(a Tan[\[Phi]])/b]]^2])

(b^2 + a^2 Tan[\[Phi]]^2))] /. \[Phi] -> ArcTan[x, y]

// TrigToExp // Simplify

// # /. {x -> Cos[\[Phi]], y -> Sin[\[Phi]]} &

// TrigToExp // Simplify // FullSimplify

$2 \sqrt{\frac{a^2 b^2}{\left(\left(b^2-a^2\right) \cos (2 \phi )+a^2+b^2\right) \left(1+\sqrt{\frac{\left(\left(a^2+b^2\right) \cos (2 \phi )-a^2+b^2\right)^2}{\left(\left(b^2-a^2\right) \cos (2 \phi )+a^2+b^2\right)^2}}\right)}}$

Заключение

Как видите, даже в такой простой и банальной вещи как многоугольник, можно найти и придумать что-то новое. И на этом история не заканчивается осталась неизвестной формула площади для общего случая, осталась неизвестной формула для произвольного, а не только правильного многоугольника, остались без рассмотрения разложения в степенные и тригонометрические ряды. Также, вероятно, подобного рода формула существует и для 3-мерного случая.

Поэтому если вам говорят, что в математике уже всё придумано и остались лишь задачи недоступные пониманию обычного человека не верьте. Есть много сугубо практических задач, о существовании которых настоящие математики не подозревают, или их решение им не интересно из-за отсутствия достаточного хайпа вокруг них, или потому что у них есть примерное представление путей достижения для их решения. Не бойтесь браться за задачи, решение которых отсутствует в википедии, не бойтесь публиковать их решения и не бойтесь читать комментарии под статьями о бесполезности всего сущего.

Подробнее..

Категории: Алгоритмы , Графический дизайн , Математика , Комплексные числа , Wolfram mathematica , Полярные координаты , Звезда , Многоугольник , Прямоугольник , Квадрат , Квадрокруг

Перевод Решение 340-символьного шифра Зодиака с помощью Mathematica

27.03.2021 12:17:15 |

Автор: admin

Зодиак (неопознанный американский серийный убийца, действовавший в 60-х и 70-х годах прошлого века) отправил множество издевательских писем в прессу города Сан-Франциско. В этих письмах убийца брал на себя ответственность за преступления и угрожал совершить новые убийства. Письма также содержали три шифра, каждый из которых являлся частью 408-символьной криптограммы. Убийца утверждал, что эта криптограмма раскроет секрет его личности. Зодиак отправил четвертый и последний шифр (который рассматривается в этой статье) в San Francisco Chronicle после того, как 408-символьная криптограмма, расшифрованная в 1969 году, не раскрыла личность убийцы.

Коротко о Z340

Меня вдохновило видео Дэвида Оранчака, в котором рассматривается 340-символьный шифр Зодиака (Z340). Этот шифр один из святых Граалей криптографии, так как его не могли разгадать на протяжении 50 лет.

340-символьный шифр Зодиака

В своем видео Дэвид высказал идею о том, что Z340 это одновременно и омофоническая замена, и перестановочный шифр. На данный момент существуют различные эффективные программы для решения омофонических шифров и лучшей из них считается AZdecrypt. Эксперименты показывают, что AZdecrypt способна решить все омофонические шифры с той же длиной и распределением символов, что и у Z340. Но, к сожалению, AZdecrypt не может расшифровать его. Возможно, решение заключается в поиске правильного перестановочного шифра с последующим использованием AZdecrypt для решения омофонического шифра замены.

Период-19

Дэвид выделил одну конкретную перестановку, которую нашли независимо друг от друга и разместили на zodiackillersite.com пользователь daikon и Ярл ван Эйке (автор AZdecrypt) период-19.

Про период

Период это расстояние или шаг между исходной позицией символа в тексте и его новой позицией после перестановки.

Ради интереса я решил построить её с помощью Mathematica:

Таблица показывает, на какую позицию должен встать символ исходного текста после перестановки

Однако это не было похоже на перестановку, которую нашли daikon и Ярл ван Эйке. К моему удивлению, оказалось, что в их перестановке при переходе с последней строки на первую использовался период, равный 18.

Перестановка с периодом 19, которую нашли daikon и Ярл ван Эйке.

Хотя эта перестановка внешне выглядела интересно, она не показалась мне естественной конструкцией, которую можно сделать на листе бумаги. Стоит отметить, что Z340 был составлен в 1969 году и поэтому наверняка он создавался вручную без использования компьютера.

Я увидел связь между перестановкой с периодом 19 и 1,2-децимацией шифра 20x17.

Что такое децимация?

Здесь и далее в тексте децимация (англ. decimation) это перестановка, построенная по следующим правилам: число, характеризующее децимацию (стоящие перед ней) определяют позицию следующего символа. В случае одномерной децимации (n-децимация) число n определяет количество шагов, которые необходимо сделать вправо, чтобы перейти к следующему символу. В случае двумерной децимации (n, m-децимация) для того, чтобы перейти к следующему символу, необходимо сделать n шагов вниз и m шагов вправо, начиная с верхнего левого угла.

Эта перестановка принимает диагонали, аналогичные перестановке с периодом 19:

Выполнение 1,2-децимации Z340 через AZdecrypt не дало решения.

Подсчет биграмм

Один из способов исследовать вероятность нахождения правильной перестановки омофонического шифра замены это подсчет количества повторяющихся биграмм.

Что такое биграмма?

Биграмма - это последовательность из двух рядом стоящих символов.

В системе Mathematica легко написать код для произвольных n-грамм:

Затем мы можем построить большое количество шифров, подобных Z340, и сравнить распределение числа биграмм в них с большим количеством случайных перетасовок Z340:

Среднее количество биграмм для случайных перетасовок составило 19,8, а для случайных шифров, подобных Z340, 34,5. Z340 имеет 25 повторяющихся биграмм, в то время как перестановка с периодом 19, которую нашли daikon и Ярл, и 1,2 децимация имеют 37 повторяющихся биграмм. Таким образом, статистически можно предположить, что мы находимся на правильном пути.

Перебор возможных перестановок

После того, как прогон 1,2-децимации через AZdecrypt не дал решения, мы решили работать над поиском среди большого числа потенциальных перестановок. Было сложно выяснить, какие перестановки проверялись в прошлом, поэтому я решил пронумеровать все приемлемые перестановки, отсортировать их по количеству биграмм и пропустить через AZdecrypt. Вот, некоторые из этих перестановок:

Я также включил все перестановки, соответствующие одномерным и двумерным децимациям. Для одномерных перечислений всех чисел, взаимно простых с 340 (чтобы заполнить весь массив) у нас есть следующие 128 соответствующих децимаций:

Для двумерных перечислений у нас есть следующие 128 соответствующих децимаций:

Например, 3,4-децимация порождает следующую перестановку:

Используя AZdecrypt, мы протестировали все перестановки с разными правилами расположения элементов: row-major, column-major, чередование строк и столбцов, чередование столбцов и строк, по внешним и внутренним спиралям, по диагоналям, а также построенные выше одномерные и двумерные децимации. Эксперимент не дал ничего похожего на решение, поэтому мы протестировали все пары перестановок. Затем мы рассмотрели возможность тестирования всех упорядоченных троек перестановок; однако для этого потребуется проверить 155 929 364 660 224 потенциальных шифров. Если предположить, что проверка одного шифра занимает одну секунду, то для полного перебора потребовалось бы более пяти миллионов лет. Поэтому мы решили ограничиться децимациями, которые можно было бы составить от руки, а затем протестировали потенциальные шифры с большим количеством биграмм. И этот поиск тоже ничего не дал.

Сегментация исходного шифра

Возможно, мы упускаем еще один шаг. Учитывая то, что 408-символьный шифр Зодиака был отправлен в виде трех одинаковых по размеру фрагментов, мы предположили, что Z340 построен из отдельных сегментов, а затем зашифрован с перестановкой и омофонической заменой:

408-символьный шифр Зодиака

Мы рассмотрели разделение шифра на несколько сегментов:

Затем мы использовали Reduce для вычисления всех возможных 2x2 сегментов:

Учитывая большое количество биграмм в 1,2-децимации, мы начали поиск с двумерных децимаций, при этом каждый сегмент имел одинаковую (одиночную) перестановку. Как и при предыдущих попытках, это ничего не дало.

Поиск композиций из нескольких перестановок и всех комбинаций перестановок для всех сегментов будет значительно более масштабным мероприятием. Поэтому мы решили повторно проанализировать результаты первоначального поиска. Из 650 000 протестированных перестановок одна содержала несколько особенно интересных сегментов открытого текста:

Это было интересно, поскольку тестируемой перестановкой оказалась 1,2-децимация с разделением шифра на три вертикальных сегмента:

Исследуя этот результат, Дэвид использовал полученное разделение, 1,2-децимацию и AZdecrypt с известными фрагментами текста: HOPE YOU ARE, TRYING TO CATCH ME и THE GAS CHAMBER. С помощью этого AZdecrypt нашел следующее решение для первого сегмента:

Эврика! Спустя 51 год мы расшифровали часть Z340. Это был особенный момент. А как насчет оставшихся двух сегментов? Возможно, мы нашли только одно правильное вертикальное разделение из 9 строк, а оставшиеся 11 строк требовали другой сегментации. Или, возможно, требовалась другая перестановка, или даже другой ключ для шифра подстановки, отличающийся от полученного для первого сегмента, или все вместе взятое. Наша работа была далека от завершения.

Дальнейший криптоанализ

Дэвид обнаружил, что мы можем использовать ключ из первого сегмента к последнему сегменту для создания следующего открытого текста без каких-либо перестановок:

Открытый текст, включая некоторые пробелы, выглядит так:

Затем, перевернем некоторые слова:

Это показалось вполне реалистичной расшифровкой последнего сегмента.

А как насчет второго сегмента? Если использовать в виде crib-фразы весь разборчивый текст из первого сегмента, мы получим следующую расшифровку:

Некоторые части этого текста имели смысл, но мы, конечно, еще не достигли желаемого результат. Мы попросили Ярла ван Эйке, автора AZdecrypt, помочь нам с этим сегментом. Он сделал следующие наблюдения:

Открытый текст LIFEIS исключается из 1,2-децимации и читается слева направо.
Многочисленные орфографические ошибки исправляются, если H в шестой строке переместить в четвертый столбец.
Нужно применить 1,2-децимацию, пропуская позиции, содержащие LIFEIS:

Тогда второй сегмент станет таким:

Ключ шифра и перестановка, которые мы обнаружили для шифра Z340, выглядят следующим образом:

Эпилог

Полное послание в примерном переводе звучит так:

Надеюсь, вы повеселились, пытаясь меня поймать. Это был не я на ТВ-шоу. Кстати, обо мне. Я не боюсь газовой камеры, потому что она отправит меня в рай пораньше, и потому что у меня есть достаточно рабов, которые будут работать на меня там, где ни у кого другого нет ничего, когда они прибывают в рай. Поэтому они боятся смерти. А я не боюсь, потому что я знаю, что моя новая жизнь будет легкой в раю. Смерть.

Спустя пятьдесят один год после того, как Зодиак отправил этот шифр в San Francisco Chronicle, у нас появилось решение. Дэвид отправил его в отдел криптоанализа ФБР в субботу, 5 декабря 2020 г. Вскоре после этого ФБР официально подтвердило правильность нашего решения.

По сути, вся моя работа над Z340 выполнялась в системе Mathematica. Я использовал кластер высокопроизводительных вычислений Spartan в Мельбурнском университете, чтобы исключить возможные перестановки с помощью zkdecrypto, а Дэвид использовал AZdecrypt. В остальном весь статистический анализ Z340, а также создание и анализ миллионов возможных перестановок были выполнены с помощью Mathematica. Причина, по которой я использовал Mathematica, проста: это самый оптимальный и эффективный инструмент для решения данной задачи.

Подробнее..

Категории: Математика , Криптография , Шифр , Омофоническая замена , Wolfram mathematica , Блог компании itsoft , Зодиак , Перестановочный шифр

	Русский
	English

Wolfram mathematica

Циркулярные кривые 2-го порядка

Кривые Безье

Циркулярные кривые

Дуга окружности

Дуга эллипса

Дуга гипотрохоиды

Алгоритм

Циркулярные сплайны

Замечания и нюансы

Заключение

Как нарисовать звезду (и не только) в полярных координатах

Комплексная форма и модификации

Квадрокруги и прочее

Переход к декартовым координатам

Appendix: как была получена формула

Заключение

Перевод Решение 340-символьного шифра Зодиака с помощью Mathematica

Коротко о Z340

Период-19

Подсчет биграмм

Перебор возможных перестановок

Сегментация исходного шифра

Дальнейший криптоанализ

Эпилог

Категории

Последние комментарии